В начале статьи приводится краткая биография А.Б. Шидловского. Затем рассказано об истоках метода — теоремах Эрмита и Линдемана. Формулируются основные определения и результаты работ К. Зигеля 1929 и 1949 годов. Дано определение 𝐸− функции и
условия нормальности совокупности функций, приведены примеры. Рассказ о работах А.Б.
Шидловского начат с условия неприводимости системы функций. Затем сформулированы три основные теоремы А.Б. Шидловского и их основные следствия. Приведена теорема о линейной независимости значений совокупности 𝐸− функций, с коэффициентами из мнимого квадратичного поля. Сформулирована аналогичная теорема в случае произвольных алгебраических коэффициентов. Сформулирована гипотеза К. Зигеля о структуре множества 𝐸− функций, удовлетворяющих дифференциальным уравнениям, и рассказано о её
решении. Приведены формулировки теорем, при условиях которых обобщённые гипергеометрические функции алгебраически независимы над полем рациональных функций, а их значения в алгебраических точках алгебраически независимы. Рассказано о количественных задачах — оценках мер линейной и алгебраической независимости значений функций.
Приведены неулучшаемые оценки. Рассмотрен ещё один класс функций, к которому можно применить метод Зигеля – Шидловского, класс 𝐺−функций. Сформулировано условие сокращения факториалов, выполняющееся для всех рассматриваемых 𝐺− функций. Приведено понятие глобального соотношения и рассказано о возможности его применения к рядам, расходящимся в поле комплексных чисел. Рассказано об арифметической природе просуммированых расходящихся рядов.

В этой обзорной статье рассматриваются различные подходы к явному описанию символа Гильберта и их обобщения на 𝑝-адические представления в рамках 𝑝-адической теории Ходжа.

Данная статья посвящена исследованию ассоциированных модулей и порядков Галуа для вполне разветвленных расширений полей дискретного нормирования. Основное внимание уделяется явным вычислениям и построению базисов для этих модулей, в частности
в случае элементарных абелевых расширений степени 𝑝2. Авторы вводят и развивают теорию градуированно-независимых множеств и диагональных базисов, которые позволяют явно описывать модули 𝛾𝑖 и соответствующие ассоциированные порядки. Центральный результат работы — теорема 3.3.2, которая дает явное описание модулей 𝛾𝑖 для расширений с группой Галуа (Z/𝑝Z)2 и различными по модулю 𝑝2 скачками ветвления. В работе
исследованы свойства введенных конструкций, в том числе их поведение относительно подъема на ручные расширения и связь с классическими ассоциированными порядками.
Полученные результаты обобщаются на случай относительных ассоциированных модулей 𝛾0𝑖 = 𝛾𝑖 ∩𝑘0[𝐺], где 𝑘0 ⊂ 𝑘. В работе используется построенный ранее первым автором изоморфизм между между 𝐾 ⊗𝑘 𝐾 и 𝐾[𝐺], и представлен детальный анализ фильтраций на тензорных квадратах и их связи со структурой модулей Галуа. Статья может представлять интерес для специалистов по теории чисел и арифметической геометрии.

Получено полное описание 𝐵𝑉 -структуры на когомологиях Хохшильда для локальных алгебр полудиэдрального типа над алгебраически замкнутым полем характеристики 2, которые по классификации Эрдманн описываются параметром 𝑘, для случая чётного параметра 𝑘 > 3. Для этого применяются метод сравнивающих морфизмов и метод стягивающих гомотопий.

Обобщённые формальные группы Хонды являются следующей ступенью в цепочке обобщений мультипликативная формальная группа – формальные группы Любина – Тейта — относительные формальные группы Любина – Тейта — формальные группы Хонды.
Этой работой мы продолжаем исследование свойств этого класса формальных групп, фокусируясь на их гомоморфизмах. В частности показывается, что гомоморфизм обобщённых формальных групп Хонды представляется в виде композиции цепочки выделенных
изогений и изоморфизма. С учётом предыдущих результатов это означает, что для обобщённой формальной группы Хонды конечной высоты существует только конечное чис-
ло изогенных попарно неизоморфных формальных групп. Полученные результаты дают представление о том, как могут быть устроены гомоморфизмы формальных групп над
произвольным 𝑝-адическим кольцом целых.

Статья посвящена применению наборов уравнений Артина – Шрайера для задания 𝑝-расширений Галуа полных дискретно нормированных полей смешанной характеристики.
Наряду с обзором известных результатов в этом направлении получены некоторые новые результаты для абелевых 2-расширений. Кроме того, продолжено изучение почти максимально разветвлённых расширений, которые были введены С. В. Востоковым при изучении аддитивных модулей Галуа. Доказывается, что если группа Галуа такого расширения имеет период 𝑝, она обязательно абелева.

В данной работе мы приводим новое доказательство теоремы, в которой описаны неприводимые подгруппы, порождённые корневыми подгруппами, в специальной линейной группе SL(𝑛,𝐾). Впервые это описание появилось в работе Дж. Маклафлина, которая была одной из первых в изучении порождений длинными корневыми унипотентными подгруппами в группах Шевалле. На данный момент геометрия длинных корневых унипотентных подгрупп хорошо изучена. Но остаётся много нерешённых вопросов, связанных с порождениями короткими корневыми унипотентными подгруппами. В частности, неизвестно описание неприводимых подгрупп, порождённых короткими корневыми подгруппами, в исключительных группах Шевалле над произвольным полем. В приводимом доказательстве мы рассматриваем группу SL(𝑛,𝐾) как группу Шевалле типа Aℓ. Таким образом, по мнению авторов, предложенный подход можно перенести на описание неприводимых подгрупп, порождённых короткими корневыми унипотентными подгруппами, в группах Шевалле.

Статья продолжает цикл работ первого автора, посвящённых сходимости последовательностей и рядов в многомерных локальных и полных полях.
Многомерные поля представляют собой цепочку дискретно нормированных полей, в которой каждое следующее – поле вычетов предыдущего. В итоге элементы записываются
в виде ряда, причем при использовании стандартной топологии дискретного нормирования ряды, определяющие элементы поля, не обязательно будут сходиться. Поэтому на
многомерных полных полях используют сложно сконструированную топологию Паршина, учитывающую топологии полей вычетов (см. [15], [5] и [6]). В ней ряды всех элементов многомерного поля сходятся. Однако и в топологии Паршина не выполнено другое важное свойство – сходимость всех степенных рядов с коэффициентами из кольца целых при подстановке вместо переменной элемента максимального идеала.
В [9] первым автором введено понятия множества сходимости – то есть такого, что ряд с коэффициентами из этого множества сходится на максимальном идеале, и доказан критерий множества сходимости. В [10] множества сходимости исследуются при помощи их мультииндексов, составляющих моноид сходимости, а в [8] конструируются кольца, являющиеся множествами сходимости, и изучаются некоторые их свойства. В данной работе выясняется, что аддитивный сдвиг множества сходимости дает множество сходимости, что любое множество сходимости секвенциально замкнуто и что сходящаяся последовательность всегда составляет множество сходимости. Эти утверждения в качестве следствия дают удобное для применения достаточное условие того, что последовательность является бесконечно малой, а также позволяют построить кольцо сходимости, которому принадлежит предел сходящейся последовательности и все ее члены.

В данной статье мы завершаем описание подгрупп, порожденных парой 2-торов в GL(𝑛,𝐾). Напомним, что 2-торами в GL(𝑛,𝐾) называются подгруппы сопряженные диа-
гональной подгруппе вида diag(𝜀, 𝜀, 1, . . . , 1). В работе [2] была доказана теорема редукции для пары 𝑚-торов. Из неё следует, что любая пара 2-торов может быть вложена в GL(6,𝐾) одновременным сопряжением. Орбита пары 2-торов (𝑋, 𝑌 ) называется орбитой в GL(𝑛,𝐾), если пара (𝑋, 𝑌 ) вкладывается в GL(𝑛,𝐾) одновременным сопряжением и не вкладывается GL(𝑛 − 1,𝐾). Ясно, что 𝑛 может принимать значения 3, 4, 5 и 6. В той же работе были описаны орбиты и порождения парами 2-торов в GL(6,𝐾). В последующих работах были описаны пары 2-торов в GL(5,𝐾), орбиты пары 2-торов в GL(4,𝐾) и порождения в GL(4,𝐾), соответствующие вырожденным случаям (редуктивная часть группы не более, чем GL(2,𝐾)). В этой работе мы описываем невырожденные случаи пар 2-торов в GL(4,𝐾) и, таким образом, завершаем описание. Наиболее сложно устроенными подгруппами оказываются группы, у которых редуктивная часть совпадает с SL(2,𝐾) × SL(2,𝐾) или SL(2,𝐿), где [𝐿 : 𝐾] = 2.

Данная статья посвящена распространеннию классического сравнения Вольстенхольма для центрального биномиального коэффициента (︀2𝑝 𝑝 )︀ на случай составного числа. Перено-
сом малой теоремы Ферма на составной случай является сравнение Гаусса, которое имеет простую комбинаторно-динамическую интерпретацию. Для распространения сравнения Вольстенхольма на составной случай необходимо использовать сравнение Якобшталя.
Приводится комбинаторное доказательство его ослабленной версии, основанное на исследовании длин орбит некоторого действия силовской 𝑝-подгруппы симметрической группы.

Пространство двумерных геометрических аделей поверхностей сильно отличается от локально компактного пространства, и на нём не существует счётно-аддитивной инвариантной по сдвигу нетривиальной меры. В то же время некоторые подфакторы аделей являются прямыми пределами компактных подфакторов или обратными пределами дискретных подфакторов, согласованными специальным образом. Используя этот факт, в статье
определяются трансляционно-инвариантная мера и интегрирование по некоторым подфакторам геометрических аделей поверхностей. Эта теория существенно отличается от теории интегрирования по аналитическим аделям поверхностей. После краткого обзора аспектов одномерной теории в статье дано полное определение двумерных геометрических аделей.
Установлен ряд их новых топологических свойств. Новая трансляционно-инвариантная мера и интегрирование по некоторым подфакторам геометрических аделей используются для интегралов от подходящих функций в двумерном методе, описывающем размер групп адельных когомологий поверхностей без использования стандартных адельных комплексов. Доказана формула для эйлеровой характеристики поверхности и её дивизора, выражающая ее через интегралы по ключевым объектам геометрических аделей. С помощью эйлеровой характеристики вводится новый двумерный адельный индекс пересечения. Для
геометрических поверхностей он является положительным кратным стандартного индекса пересечения. Приводятся новые доказательства ряда результатов, полученных в предыдущем исследовании геометрических аделей.

Заметка посвящена доказательству некоторых вариантов интерполяционной теоремы для интуиционистского исчисления предикатов без функциональных символов и равенства с интерполянтом специального вида. Наиболее интересен случай универсального хорновского интерполянта: аксиомы многих алгебраических систем задаются универсальными хорновскими формулами. Результаты, полученные в данной работе, могут быть полезны как с точки зрения теории доказательств, так и в приложениях, например, при решении задач искусственного интеллекта и разработке языков логического программирования. Заметка написана в духе теории доказательств, основным инструментом для решения задачи
служат секвенциальные исчисления и такие техники преобразования выводов, как обращение применений правил вывода, перестановка применений правил по С. К. Клини и прополка по В. П. Оревкову.
Заметка состоит из введения, разбитой на 3 параграфа основной части и заключения. Введение содержит краткий исторический обзор и обсуждение актуальности работы. В
первом параграфе основной части вводятся необходимые определения и формулируется главный результат. Второй параграф посвящён описанию построенного В. П. Оревковым секвенциального варианта интуиционистского исчисления предикатов IGL. Третий отведён доказательству основной теоремы. Заключение содержит обсуждение полученных результатов и краткий обзор перспектив дальнейшей работы.

Изучается псевдоевклидов аналог интегрируемой системы Жуковского для осесимметричного тела. На многомерном пространстве параметров системы найдены два существен-
ных параметра, в терминах которых построено разделяющее множество. В зависимости от значений параметров явно описано расположение бифуркационной кривой на плоскости значений отображения момента. Вычислены аналоги инвариантов Фоменко для неособых изоэнергетических и изоинтегральных поверхностей. Приведена визуализация работы алгоритма по построению меченых графов для неособых изоэнергетических поверхностей.

Основным результатом статьи является положительное решение проблемы вхождения в группах Артина с древесной структурой.

Пусть 𝑂𝑋𝑌 — прямоугольная система координат с целочисленной решеткой, 𝐴𝐵 — отрезок с целыми (целочисленными) концами 𝐴 = (𝑞; 0)𝑂𝑋𝑌 = 𝐴(𝑞) и 𝐵 = (0; 𝑝)𝑂𝑋𝑌 = 𝐵(𝑝), такими, что 𝑝 и 𝑞 взаимно просты, а разложение 𝑝 𝑞 в цепную дробь имеет вид [0; 𝑎1, 1, 𝑎3,
. . . , 𝑎2𝑁′+1], где 𝑎−1 , 𝑎3, . . . , 𝑎2𝑁′+1, 𝑁′, 𝑝, 𝑞, ∈ N : (= {1, 2, . . .}).
Рассмотрим множество S𝐴𝐵 таких единичных квадратов (клеток) этой решетки, что внутренность каждого из них имеет непустое пересечение с 𝐴𝐵. Границу этого множества
представим в виде объединения ломаных S−𝐴𝐵 и S+
𝐴𝐵 таких, что их крайними вершинами служат точки 𝐴 и 𝐵. Здесь индекс минус (плюс) указывает на то, что S− 𝐴𝐵 (S+
𝐴𝐵) лежит по левую (правую) сторону от отрезка 𝐴𝐵 при движение от 𝐴 к 𝐵. Ломаную S− 𝐴𝐵 (S+ 𝐴𝐵) назовем левой (правой) (целочисленной) ступенчатой аппроксимацией отрезка 𝐴𝐵 или цепной дроби [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁]. Для краткости такие ломаные будем называть маршами, а их горизонтальные звенья — ступенями, вертикальные —
высотами, что вызвано ассоциацией с лестничным маршем.
В работе получены следующие результаты:
1. Формулы целочисленной аппроксимации цепной дроби, как конечных, так и бесконечных.
2. Алгоритмическое построение маршей S±
𝐴𝐵, определяемое рассматриваемой цепной
дробью, дает их аналитическое задание через марши векторов-слагаемых из второго равенства:

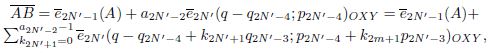
где векторы 𝑒2𝑁′−1 = (−𝑞2𝑁′−4; 𝑝2𝑁′−4)𝑂𝑋𝑌 и 𝑒2𝑁′ = (−𝑞2𝑁′−3; 𝑝2𝑁′−3)𝑂𝑋𝑌 , координаты которых определяются подходящими дробями 𝑝𝑛−3/𝑞𝑛−3 порядка 𝑛 = 2𝑁′ − − 1, 2𝑁′, исходной цепной дроби, а в скобках указаны точки приложения векторов.
3. Расположение ступеней ширины 𝑎1 в S− 𝐴𝐵, устанавливается с помощью семейства параллельных переносов отрезка с концами (𝑞 − 𝑎1; 0)𝑂𝑋𝑌 и (𝑞 − 1; 0)𝑂𝑋𝑌 . Каждый член семейства находим через аппроксимационные формулы для [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁].
4. Формула, дающая количество ступеней ширины 𝑎1 в S−
𝐴𝐵, представляет собой трехдиагональный определитель (2𝑁′ −5)-го порядка: главная диагональ состоит из элементов 𝑎4, 1, 𝑎5, . . . , 𝑎2𝑁′−6, верхняя диагональ — из единиц, нижняя из минус единиц, а остальные нули.

Введено понятие полутранзитивного бинарного действия группы 𝐺 на топологическом пространстве. Доказана теорема о двойственности полутранзитивных дистрибутивных бинарных 𝐺-пространств и топологических полей с мультипликативной группой 𝐺. Эта теорема устанавливает эквивалентность между категорией полутранзитивных дистрибутивных бинарных 𝐺-пространств и категорией топологических полей, мультипликативная
группа которых изоморфна 𝐺.
В качестве приложений теоремы двойственности установлены два важных результата. Показано, что конечная группа может действовать полутранзитивно, дистрибутивно и
бинарно только на конечных множествах, мощность которых является степенью простого числа. Также получена полная характеристика тех групп, которые могут выступать в качестве мультипликативных групп топологических полей.

Рассматриваются нелинейные сингулярно возмущенные параболические уравнения в областях с угловыми точками границы. Для построения асимптотики решения применяется нелинейный метод угловых пограничных функций. Предполагается, что в задачах, определяющих главные члены угловой части асимптотики решения, нелинейности представляют собой кубические многочлены. Существование решений этих задач основано на методе верхних и нижних барьеров, построение которых представляет основную трудность. В частности, эта трудность связана с разнообразием поведения кубических многочленов. В работе предложена классификация, основанная на выделении промежутков определенного характера монотонности и направления выпуклости.

В статье описана методика конкретизации определяющего соотношения Мурнагана, включающего в себя пять материальных констант, с помощью задачи об однородном одноосном растяжении (сжатии) образца, выполненного из нелинейно-упругого материала.
Предлагаемая методика основана на использовании экспериментально наблюдаемых значений осевой нагрузки и поперечных удлинений призматического образца в зависимости от его осевого удлинения. Экспериментальные кривые аппроксимируются теоретическими зависимостями, следующими из решения задачи растяжения-сжатия в рамках рассматриваемого определяющего соотношения. Из требования минимальных отличий между экспериментальными и теоретическими данными с помощью метода наименьших квадратов определяются материальные константы. В работе описано автоматизированное с помощью языка программирования python проведение численного эксперимента, данные которого использовались для демонстрирования выполнения предложенной конкретизации определяющего соотношения Мурнагана. Численный эксперимент был проведен в отечественном
пакете прочностного анализа CAE Fidesys. Осуществлена проверка корректности предложенной методики с помощью сравнения экспериментальных данных и теоретических,
полученных для материальных констант, определенных в рамках представленных алгоритмов конкретизации определяющего соотношения Мурнагана.

В статье приводится обзор результатов о полиадических числах Лиувилля

В статье приводится обзор результатов о полиадических числах Лиувилля

В статье для любого фиксированного 𝑐 ≥ 1 получена нижняя оценка 𝜅(𝑐), при выполнении которой к заданному действительному числу 𝑁 > 𝑁0(𝜀) можно подойти суммой
двух степеней простых чисел 𝑝𝑐1 + 𝑝𝑐 2 на расстояние не большее, чем 𝐻 = 𝑁𝜅(𝑐)+𝜀, где 𝜀 – произвольное положительное число.
Данный результат получен при помощи плотностной техники, разработанной Ю. В. Линником в 1940-х годах. Плотностная техника основана на применении явных формул, выражающих суммы по простым числам через суммы по нетривиальным нулям дзета-функции Римана и использовании плотностных теорем – оценок количества нетривиальных нулей дзета-функции, лежащих в критической полосе и таких, что их реальная часть больше некоторого 𝜎, где 1 > 𝜎 ≥ 1/2.
Содержащиеся в статье результаты основаны на применении современных плотностных теорем, полученных А. Ивичем. Кроме того, при доказательстве была использована тео-
рема Бейкера, Хармана, Пинтца: к заданному действительному числу 𝑁 > 𝑁0(𝜀) можно подойти простым числом на расстояние не большее, чем 𝐻 = 𝑁21/40+𝜀. Также использован результат М. Хаксли об оценке значений дзета-функции Римана на критической прямой: |𝜁(1/2 + 𝑖𝑡)| ≪ 𝑡32/205+𝜀.

В работе получено полное аналитическое решение задачи о свободных колебаниях струны с произвольным числом скачкообразных изменений скорости распространения волн.
Предложен новый комбинаторно-аналитический метод, позволяющий представить решение в виде компактной явной формулы. Доказано, что решение представляет собой суперпозицию 2𝑁−1 волн, каждая из которых соответствует одному из возможных путей распространения возмущения через моменты переключения скорости.
Установлено, что коэффициенты в полученной формуле имеют ясный физический смысл и представляют собой произведения коэффициентов прохождения и отражения на
границах раздела сред. Метод обобщен на случай конечной струны с нулевыми граничными условиями Дирихле.
Решение построено в замкнутой форме и подтверждено двумя независимыми методами: методом Фурье и методом математической индукции. Полученные результаты позволяют анализировать сложные волновые процессы в средах с кусочно-постоянными параметрами и могут быть использованы в задачах акустики, сейсмологии и теории управления.

метода исследования динамики производных различных порядков сингулярно совершенного дифференциального уравнения. В методе предварительного интегрирования высшей производной уравнения и правая часть представляются в виде конечных рядов по полиномам Чебышева первого рода с неизвестными коэффициентами разложения. Перед решением задачи выбранный ряд предварительно интегрируется и находятся выражения
в виде рядов для всех низших производных и искомого решения. Неизвестные постоянные, появляющиеся при интегрировании ряда, определяются из дополнительных условий задачи. Неизвестные коэффициенты определяются из системы алгебраических уравнений и, подставляя их в нужный ряд, вычисляются производные и решение задачи.

В статье рассматривается спектральный метод оценки эффективных свойств композитов и кернов на основе быстрого преобразования Фурье (FFT). Имея ограничения на
прикладываемые граничные условия, метод предлагает высокую эффективность анализа напряжений и деформаций в периодической ячейке за счет асимптотики FFT по времени 𝑂(𝑛 · 𝑙𝑜𝑔(𝑛)). Проведённое сравнение результатов гомогенизации с Методом Конечных Элементов показывает высокую точность спектрального метода при оценке свойств керна. Представлен анализ эффективности и сходимости алгоритма для различных периодических ячеек и материалов.

Суммирование мультипликативных функций встречается едва ли не в половине задач аналитической теории чисел. Центральное место в вопросе суммирования значений мультипликативных функций занимают вопросы об асимптотическом поведении сумм вида

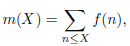
при 𝑋 → ∞, где 𝑓(𝑛) — мультипликативная функция натурального аргумента. Настоящая статья посвящена исследованию суммированием мультипликативных функций по числам, простые делители которых лежат в заданных интервалах. Получена асимптотическая формула для сумм произведения мультипликативных функций, простые делители которых лежат в заданных интервалах.

Исследуется задача нахождения орбит группы 𝐺𝐿(𝑉 ) на пространстве 𝐴𝑙𝑔(𝑉 ) всех билинейных отображений 𝑉 ×𝑉 → 𝑉. В работе рассматриваются только двумерные алгебры
над полем Z2 без использования методов теории инвариантов. Рассматривается классификация алгебр с новых позиций. Для выделения большого класса алгебр используется отображение 𝑃, которое естественно возникает как отображение 𝐴𝑙𝑔(𝑉 ) → 𝑉 * × 𝑉 *, сопоставляющее каждой структуре алгебры на пространстве 𝑉 пару линейных форм 𝑇𝑟1 и 𝑇𝑟2, задаваемых как следы операторов левого и правого умножения в этой алгебре. Изучено 𝜏 -действие группы 𝐺𝐿(2,Z2), состоящей из невырожденных квадратных матриц 𝑔, на множество MSC(A) — матрицы структурных констант. Данное действие в общем виде записывается как 𝜏 : (𝑔,MSC(A)) → 𝑔MSC(A)(𝑔−1)⊗2. Действие 𝜏 задаёт экви-
валентность между матричными операторами двумерных алгебр и определяет структуру для описания орбит действия. Для данного действия было использовано 𝑃-отображение,
которое имеет вид 𝑃(𝜏 (𝑔,MSC(A))) = 𝑃(MSC(A))𝑔−1.
Для матричных представителей двумерных алгебр предложена полная матричная классификация с различными орбитами над Z2. Изложена связь 𝑃(𝑔MSC(A)(𝑔−1)⊗2) = 𝑒,
между MSC(A) и задающей ее линейно независимой системой {𝑇𝑟𝑘} = {𝑇𝑟1, 𝑇𝑟2}. Данная связь различных матричных представителей орбит равна 𝑞4. В работе также учтена связь того, что матричные представители орбит при действии 𝜏 могут пересекаться, однако в исследовании строго доказана их непересекаемость.
Показана взаимосвязь в виде системы равенств между элементами эквивалентных орбит 𝜏-действия группой 𝐺𝐿(2,Z2) на MSC(A) для дальнейшего изучения над полями более высшего порядка. Результаты показывают, что количество различных орбит 𝜏-действия равняется 52. Как следствие в теоретико-групповом смысле, данная задача эквивалентна описанию умножения на двупорожденной абелевой группе вида Z2 ⊕ Z2 с точностью до
изоморфизма.
В заключение приводятся некоторые свойства решётки Z𝑞 × Z𝑞 (𝑇𝑟𝑘) с использованием системы векторов {𝑇𝑟𝑘}, из которых, в частности, следует описание эквивалентных матриц с точностью до числа по пяти непересекающимся линейным формам {𝑇𝑟𝑘} = {𝑇𝑟1(MSC(A)), 𝑇𝑟2(MSC(A))} = {𝑇𝑟1(𝐴), 𝑇𝑟2(𝐴)} двойственного пространства алгебры A.

Доказаны теоремы об оценках линейных форм от значений обобщённых гипергеометрических рядов вида
Σ︀∞𝑛=0 (𝛼1)𝑛 . . . (𝛼𝑚−1)𝑛 𝑧𝑛, среди параметров которых трансцендентные полиадические числа Лиувилля

Изучается псевдоевклидов аналог интегрируемой системы Жуковского для осесимметричного тела. На многомерном пространстве параметров системы найдены два существенных параметра, в терминах которых построено разделяющее множество. В зависимости от значений параметров явно описано расположение бифуркационной кривой на плоскости значений отображения момента. Вычислены аналоги инвариантов Фоменко для неособых изоэнергетических и изоинтегральных поверхностей. Приведена визуализация работы алгоритма по построению меченых графов для неособых изоэнергетических поверхностей.

Изучены графики фаз квазиклассических асимптотик решений двумерного безмассового уравнения Дирака с локализованным начальном условием в постоянном (не зависящим ни от точки, ни от времени) электромагнитном поле. Рассматриваемое уравнение описывает распространение квазичастиц (электронов и дырок) в графене, при этом электрическая компонента поля параллельна плоскости графена, а магнитная — перпендикулярна ей. Получены формулы для фаз при всех значениях компонент электромагнитного поля.

Рассмотрена численная оценка трещиностойкости листовых заготовок из титанового сплава с различной микроструктурой, соединенных сваркой давлением в режиме сверхпластичности. Структурно-механическая модель рассматриваемого объекта представлена в виде графа. На основе функционального осреднения реализован итерационный метод нахождения параметров напряжений и деформаций для его вершин в виде обобщения метода Ньютона. Приведенные результаты математического анализа механики зарождения и развития трещины в двуслойной сварной заготовке из титанового сплава ВТ6 с принципиально различной микроструктурой указывает на перспективность использования таких слоистых титановых композиций в изделиях ответственного назначения с целью повышения их конструктивной прочности.

Авторы статьи ставят перед собой задачу: ознакомить математическую общественность с математическим творчеством некоторых иностранцев – выпускников таких российских вузов, как Финансовый университет при Правительстве Российской Федерации, Московский технический университет связи и информатики, в которых работают авторы статьи.
Авторы закончили Тульский государственный педагогический университет им. Л. Н. Толстого и не могли не вспомнить иностранных выпускников периода СССР. Влияние российского образования на математическое творчество иностранных выпускников российских вузов заслуживает особого внимания.
Россия славится своими достижениями в области математики, высоким уровнем её преподавания. Российское математическое образование оказывает значительное влияние на иностранных выпускников, на международное научное сотрудничество. Исторические достижения, участие в международных проектах, совместные проекты, публикации и преподавание за рубежом – все это способствует укреплению связей между российскими и
зарубежными учеными, обогащая мировую науку новыми идеями и открытиями. Некоторые иностранные выпускники российских вузов сделали выдающуюся карьеру. Напри-
мер, Хамадун Туре работал генеральным секретарем Международного союза электросвязи, специализированного учреждения ООН, занимающегося вопросами информационно-коммуникационных технологий. В списке литературы перечислены работы иностранных выпускников.

В статье описана методика моделирования в программной среде COMSOL (ПК COMSOL Multiphysics) температурных параметров лазерного воздействия, позволяющего без разрушения поверхностного слоя стального изделия очистить его поверхность от окалины, оптимизировать микроструктуру и повысить физико-механические свойства рабочих поверхностей проката из углеродистой стали.
На основании теоретических представлений о тепловых процессах, определяющих энергетическое и температурное воздействие лазерного излучения, в результате моделирования были разработаны уравнения температуры локального нагрева обрабатываемой поверхности и площади покрытия излучением в единицу времени. С их использованием в численном эксперименте были определены характеристики термических циклов нагрева охлаждения при лазерном сканировании в ходе очистки поверхности образцов проката из стали марки 20 от окалины, состоящей из магнетита (Fe3O4). Получены значения температур нагрева окалины и стали в процессе очистки, а также определено их распределение на различной
глубине окалины и стали при многократном сканировании пучком непрерывного лазера. Выявлена незначительная аккумуляция тепловой энергии от ближайших по времени
термоциклов (проходов лазерного сканирования). За время всех термоциклов зафиксировано увеличение стационарной температуры поверхности образцов всего на 100 градусов,
что не влияет на структурную стабильность стальной поверхности.
Результаты исследований послужили основой для оформления патента РФ на способ лазерной микрообработки сталей (RU 2 836 694 C1).

В статье описана методика моделирования в программной среде COMSOL (ПК COMSOL Multiphysics ) энергетических параметров лазерного воздействия, позволяющего
без разрушения поверхностного слоя оптимизировать микроструктуру и повысить физико-механические свойства рабочих поверхностей деталей из углеродистых сталей.
На основании теоретических представлений о механизмах основных процессов, определяющих энергетические характеристики воздействие лазерного излучения, были получены уравнения средней плотности энергии (энергетической дозы) лазерного излучения, температуры локального нагрева в центре пятна сканирования обрабатываемой поверхности, а также площади покрытия излучением в единицу времени и скорости её покрытия из-
лучением, достаточной для изменения микроструктуры углеродистой стали без разрушения поверхностного слоя. На основании их экспериментальной апробации были разработаны режимы лазерного воздействия (микроструктурирования), обеспечившие возможность
управления диффузией углерода из внутренних слоев детали к её рабочим поверхностям. Реализация разработанных режимов позволила сформировать структуру поверхностного слоя с повышенным содержанием углерода и высокой твердостью без оплавления за счёт
диффузии углерода из внутренних слоев к рабочим поверхностям изделий. Результаты исследований послужили основой для оформления патента РФ на способ лазерной микрообработки сталей (RU 2 840 325 C1).

В работе строится программа нахождения наилучших совместных приближений второго рода для зависимых иррациональностей.
Приводятся результаты расчётов в системе компьютерной математики mathcad15, которые подтверждают выводы работы [2], что начиная с некоторого места все совместные
наилучшие приближения второго рода зависимых случайных величин определяются знаменателями подходящих дробей основной иррациональности, которой кратны все остальные.

В 1963 году Хоули [1] (см. также [2]), опираясь на оценки средних тригонометрических сумм по решениям квадратичных сравнений, впервые доказал асимптотическую формулу для средних числа делителей квадратичного полинома со степенным понижением в остаточном члене. Позднее эти результаты были усилены в работах [3] и [4]. В настоящей
работе мы доказываем более сильные результаты на эту тему.

В работе изучаются наилучшие совместные приближения второго рода для линейно зависимых иррациональностей. Показано, что начиная с некоторого места они определяются
подходящими дробями к первой иррациональности, которой кратны все остальные.

Цель работы — построение датчиков псевдослучайных чисел на основе разложений почти полиадических чисел по степеням заданного числа. Полиадическим числом при-
нято называть ряд вида Σ︀∞ 𝑛=0 𝑎𝑛𝑛!, где 0 ⩽ 𝑎𝑛 ⩽ 𝑛, 𝑎𝑛 — целое число. Ряды подобного вида, сходящиеся во всех полях 𝑝–адических чисел, кроме конечного их числа, имеющие рациональные коэффициенты, называются почти полиадическими числами. Рассмотрим функциональные ряды вида Σ︀∞ 𝑛=0 (𝜆)𝑛𝑧𝑛, где (𝜆)0 = 1, (𝜆)𝑛 = 𝜆 (𝜆 + 1) . . .
(𝜆 + 𝑛 − 1), т.е. (𝜆)𝑛 – символ Похгаммера, а 𝜆 – рациональное число. Эти ряды, отличные от многочленов, имеют нулевой радиус сходимости в поле комплексных чисел, однако они
имеют радиусы сходимости, большие 1 в любом поле 𝑝 – адических чисел, кроме конечного числа полей 𝑝 – адических чисел, тех, в которых 𝑝 входит в знаменатель несократимой
дроби 𝜆. Будем считать, что 𝜆𝑖 = 𝑎𝑖 𝑏𝑖 , 𝑖 = 1, . . . ,𝑚, где 𝑎𝑖, 𝑏𝑖 – натуральные числа, Н.О.Д. (𝑎𝑖, 𝑏𝑖) = 1, 𝑖 = 1, . . . ,𝑚 и 𝜆𝑖 − 𝜆𝑗 ̸∈ Z при 𝑖 ̸= 𝑗. Можно доказать, что при этих условиях ряды
Σ︀∞ 𝑛=0 (𝜆𝑖)𝑛(𝑏𝑖)𝑛𝑍𝑛, 𝑖 = 1, . . . ,𝑚 алгебраически независимы над полем рациональных функций от 𝑧 [1].
Σ︀ Из этого следует бесконечная алгебраическая независимость полиадических чисел ∞ 𝑛=0 (𝜆𝑖)𝑛(𝑏𝑖)𝑛, 𝑖 = 1, . . . ,𝑚 [2].
Σ︀ Можно высказать предположение о том, что цифры разложений частичных сумм 𝑁 𝑛=0 (𝜆𝑖)𝑛(𝑏𝑖)𝑛, 𝑖 = 1, . . . ,𝑚 рассматриваемых рядов обладают неплохими статистическими свойствами. В статье описаны результаты проведённых экспериментов.

Рассмотрим последовательности целых чисел 𝑎(𝑘,𝑗)
𝑛 , 𝑗 = 1, ..., 𝑚, 𝑘 = 1, ..., 𝑇𝑗 , удовлетворяющие условиям

𝑎(𝑘,𝑗)𝑛 = 𝑎(𝑘,𝑗)𝑛+𝑇𝑗, 𝑗 = 1, ..., 𝑚, 𝑘 = 1, ..., 𝑇𝑗 , 𝑛 = 0, 1, ...

и рассмотрим функции

𝐹𝑗,𝑘(𝑧) =∞Σ︁𝑛=0𝑎(𝑘,𝑗)𝑛𝑛!𝑧𝑛, 𝑗 = 1, ..., 𝑚, 𝑘 = 1, ..., 𝑇𝑗 .

В работе устанавливаются условия, при которых совокупность функций

1, 𝑒𝑧, 𝐹𝑗,𝑘(𝑧), 𝑗 = 1, ..., 𝑚, 𝑘 = 2, ..., 𝑇𝑗

линейно независима над C(𝑧) и для любого рационального числа 𝛾 ̸= 0 их значения в точке 𝛾 линейно независимы. Получена оценка меры линейной независимости этих чисел.
Результат может быть использован при построении псевдослучайных чисел.

В данной работе мы используем статистическое компактное подпространство в качестве инструмента для введения понятия монотонного звездного s-компактного пространства.
Это развивает работы С.Г. Попвасилева, Дж.Э. Портера, М. Матвеева, Л. Жункейры, Р. Уилсона, О. Аласа, Дж. ван Милла и В. Ткачука. Наряду со сравнением с различными формами компактности исследуются некоторые сохраняющие свойства монотонной звездной s-компактности. Более того, с помощью свойства 𝛿0-пересечения установлена характеристика пространства как конечного пересечения.