Сумма произведений мультипликативных функций по числам, простые делители которых лежат в заданных интервалах
https://doi.org/10.22405/2226-8383-2025-26-4-383-397
Аннотация
Суммирование мультипликативных функций встречается едва ли не в половине задач аналитической теории чисел. Центральное место в вопросе суммирования значений мультипликативных функций занимают вопросы об асимптотическом поведении сумм вида
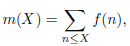
при 𝑋 → ∞, где 𝑓(𝑛) — мультипликативная функция натурального аргумента. Настоящая статья посвящена исследованию суммированием мультипликативных функций по числам, простые делители которых лежат в заданных интервалах. Получена асимптотическая формула для сумм произведения мультипликативных функций, простые делители которых лежат в заданных интервалах.
Об авторе
Умидилла Чариевич Чариев
Таджикский государственный педагогический университет им. Садриддина Айни
Таджикистан
Таджикистан
кандидат физико-математических наук
Список литературы
1. Бухштаб А. А. Асимптотическая оценка одной общей теоретико-числовой функции. //А.А. Бухштаб / Матем. сб.2, (44):6, 1937. C. 1239 – 1246.
2. Бухштаб А. А. О числах арифметической прогрессии, у которого все простые множители малы по порядку роста. //А.А. Бухштаб / ДАН СССР, Т. 67, № 1, 1949. C. 5 – 8.
3. Бухштаб А. А. Об асимптотической оценке числа чисел арифметической прогрессии, не делящихся на «относительно» малые простые числа. //А.А. Бухштаб / Матем. сб.28(70):16, 1951. C. 165 – 184.
4. Виноградов И. М. О числах с малыми простыми делителями. //И.М. Виноградов/ ДАН СССР, Т. 109, № 4, 1956. C. 683 – 686.
5. Линник Ю. В. Замечания о наименьшем квадратичном невычете. //Ю.В. Линник/ ДАН СССР, Т. 36, вып.4–5, 1942. C. 131 – 132.
6. Левин Б. В. Об одном классе задач теории чисел, сводящихся к дифференциальным уравнениям с запаздывающим аргументом. //Б.В.Левин, А.С.Файнлейб// Науч. тр. Ташкентского универс.та, вып.228, 1963. C. 56 – 69.
7. De Bruijn. The asymptotic behaviour of a function occurring in the theory of primes.//De Bruijn/ Journ. Indian Math.Soc.15, 1951. P. 25 – 32.
8. Rankin R. A. The difference between consecutive prime numbers.//Rankin R. A./ Journ London, Math.Soc., 13, 1938. P. 242 – 247.
9. Левин Б. В. Применение некоторых интегральных уравнений к вопросам теории чисел. //Б.В.Левин, А.С.Файнлейб// Успехи математических наук. Т. 22. № 3(135), 1967. C. 119 – 199.
10. Friedldnder John B. Integers free from large and small primes.//John B. Friedlander // Proc. London Math. Soc. 33, № 3, 1976. P. 565 – 575.
11. Чариев У. Асимптотические поведение решений некоторых дифференциально-разностных уравнений. //У.Чариев // ДАН Тадж. ССР, Т. 22. № 8. 1979. C. 463 – 465.
Рецензия
Для цитирования:
Чариев У.Ч. Сумма произведений мультипликативных функций по числам, простые делители которых лежат в заданных интервалах. Чебышевский сборник. 2025;26(4):383-397. https://doi.org/10.22405/2226-8383-2025-26-4-383-397
For citation:
Chariyev U.Ch. The sum of the products of multiplicative functions over numbers whose prime divisors lie in the specified intervals. Chebyshevskii Sbornik. 2025;26(4):383-397. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-4-383-397
Просмотров:
1
Послать статью по эл. почте 