Article
One of the areas of time series analysis is the study of their morphology. The results of such a study are used to detect various types of anomalies in the behavior of the series, moments of
restructuring its behavior, etc.
This paper presents a program for exploring records using DMA methods – a new researcheroriented data approach that makes extensive use of fuzzy mathematics. Its input data is a record
expressing a process with discrete time and some property of the process whose fulfillment is of interest to the researcher.
The manifestation of a property on a record is formalized as a fuzzy structure (measure of manifestation) on the do-main of the record definition, which expresses the degree of manifestation of the property in question. The measure of manifestation of a property is the
basis for dividing the record into regular, transient, and abnormal manifestations of the property in question on a record. This division gives the researcher a simple and meaningful idea of the property manifestation on a record that interests him.
The purpose of this paper is to improve on the current DMA decomposition of such a decomposition.
Under reasonably easy-to-observe restrictions on the nonlinearities, without assuming that they satisfy the Lipschitz condition, global theorems on the existence, uniqueness, and estimates of the solution for three different classes of inhomogeneous nonlinear integral equations are proved by the method of monotone (in the sense of Browder – Minty) operators. In these equations, the operators of fractional (in the sense of Riemann – Liouville) integration with
a variable external coefficient enter linearly or nonlinearly, or these operators contain a nonlinearity under the sign of the integral (Hammerstein-type equation). In the latter case, the existence and uniqueness of the solution are established without the coercivity condition on the nonlinearity. In all cases, the conditions found in the work under which the fractional integration operators with a variable external coefficient act continuously from the real Lebesgue
space 𝐿𝑝(𝑎, 𝑏) to the spaces conjugate to them and are strictly positive play an important role. The proved theorems within the framework of the space 𝐿2(𝑎, 𝑏) cover the corresponding linear equations with integrals of fractional order. From the obtained estimates, in particular,
it directly follows that under the conditions of the proved theorems, the corresponding homogeneous linear and nonlinear integral equations have only a trivial (zero) solution.
This paper is devoted to establishing the order of smoothness of 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) — the largest convex continuation to [0, 1]𝑛 of any Boolean function 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛). As a result of the study, for each Boolean function 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛), the order of differentiability of 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) — the corresponding greatest convex continuation to [0, 1]𝑛 — was established, namely, firstly, the greatest convex continuation 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) was estimated from both sides so that, which implies the continuity of 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) on [0, 1]𝑛 for any
natural 𝑛, and secondly, it was proved that if the number of essential variables of the Boolean function 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛) is less than two, then on [0, 1]𝑛 the greatest convex continuation 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) is infinite differentiable, and if there are at least two, then on [0, 1]𝑛 the largest convex continuation 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) is not differentiable, i.e. it is only continuous.
The article studies semimodules over a single-element semiring {𝑒}, which we call a trivial semiring. By a semimodule over a trivial semiring we mean a commutative semigroup ⟨𝐴,+⟩ considered together with the mapping 𝑒 : 𝐴 → 𝐴, 𝑎 → 𝑒𝑎 which is additive, i. e. 𝑒(𝑎+𝑏) = 𝑒𝑎+𝑒𝑏
for any 𝑎, 𝑏 ∈ 𝐴; and idempotent, i. e. 𝑒(𝑒𝑎) = 𝑒𝑎 for all 𝑎 ∈ 𝐴; 𝑒𝑎 + 𝑒𝑎 = 𝑒𝑎 for any 𝑎 ∈ 𝐴.
In this case, the mapping 𝑒 : 𝐴 → 𝐴, or the action of 𝑒 onto 𝐴, is called a retraction of the commutative semigroup ⟨𝐴,+⟩. For the retraction of 𝑒 onto 𝐴, the set 𝑒𝐴 will be the set of all fixed points of the mapping 𝑒, called the 𝑒-set. A commutative semigroup ⟨𝐴,+⟩ can have very
different retractions and, accordingly, different 𝑒-sets. Moreover, the same set on a semilattice 𝐴 can serve as an 𝑒-set of different retractions of 𝑒 onto 𝐴.
The article shows, using a number of examples, that it is advisable to study retractions on semilattices ⟨𝐴,+⟩, which we call e-semimodules.
The paper provides some classification of retractions, describes the structure of chain retractions. It is proved that all non-empty subsets of an arbitrary chain are 𝑒-sets if and only if this chain is discrete. We considered increasing, decreasing and linear retractions on
semilattices and lattices. It is shown that increasing retractions 𝑒 and decreasing retractions 𝑒 are uniquely determined by their 𝑒-sets.
We also obtained other results, and gave corresponding examples in the paper.
In the paper theorems on the convergence trigonometrical series over primes are proven.
We continue the G. I. Arkhipov’s and K. I. Oskolkov’s investigations on spechial trigonometric series, based on the I. M. Vinogradov’s method on estimations of H. Weyl’s trigonometric sums with polynomial in the argument of the trigonometric function.
In this paper we consider special trigonometric series over prime numbers of of three types in the dependence of functions of an argument trigonometric function: the square root, the linear
and the the general polynomial from the one variable, running sequently all prime numbers.
Here we essentially are used the I. M. Vinogradov’s estimates of trigonometric sums over prime numbers.
We note the one circumstance, that appeares the need touse the holding of Grand Riemann’s hypotheses.
Besides, in the case of linear polynomials of arguments for us required a little improvement of I. M. Vinogradov’s estimations, getting by R. C. Vaughan.
The article discusses the properties of the arithmetic derivative and the primitive on the set of rational numbers, obtained properties related to similar properties of the derivative function, some equations in arithmetic derivatives and the properties of their solutions.
In this paper, an imperative programming language considering some hardware limitations of a computer based on the RV32I instruction set is defined, including its syntax and semantics in a form of Hoare logic. The need for such language comes from the fact that formal proofs
conducted for programs in languages not considering hardware limitations cannot be directly applied to translated code running on real hardware. At the same time, conducting proofs for programs written directly in machine code is extremely laborious. The language defined in the paper takes into account such hardware limitations as finite register width, finite memory capacity and the usage of modulo arithmetic instead of regular arithmetic. The paper contains
an example of a program computing GCD of two non-negative integers, which is written in the proposed language. A proof of the program correctness is also included. Thus, the paper demonstrates that formal proofs could be conducted for programs in the language considering some hardware limitations, and the complexity of the proofs would be comparable to ones conducted for equivalent programs written in regular imperative languages, which do not take
hardware limitations into account. Directions for future work include composing an algorithm for translation of the proposed language to machine code and proving the algorithm’s correctness.
We prove that if a congruence lattice of a unar satisfies a non-trivial lattice identity, then the unar is a homomorphic image of a coproduct of finite number of lines and rays, which, in turn, is equivalent to the fact that the unar has only a finite number of connected components, knots, initial elements, and input degree of each element of the unar is finite.
We continue to study some arithmetical properties of Farey sequences by the method introduced by F. Boca, C. Cobeli and A. Zaharescu (2001). Let Φ𝑄 be the classical Farey sequence of order 𝑄. Having the fixed integers 𝐷 ⩾ 2 and 0 ⩽ 𝑐0 ⩽ 𝐷 − 1, we colour to the red
the fractions in Φ𝑄 with denominators ≡ 𝑐0 (mod𝐷). Consider the gaps in Φ𝑄 with coloured endpoints, that do not contain the fractions 𝑎/𝑞 with 𝑞 ≡ 𝑐0 (mod𝐷) inside. The question is to find the limit proportions 𝜈(𝑟;𝐷, 𝑐0) (as 𝑄 → +∞) of such gaps with precisely 𝑟 fractions inside in the whole set of the gaps under considering (𝑟 = 0, 1, 2, 3, . . .).
In fact, the expression for this proportion can be derived from the general result obtained by C. Cobeli, M. Vˆajˆaitu and A. Zaharescu (2012). However, such formula expresses 𝜈(𝑟;𝐷, 𝑐0) in the terms of areas of some polygons related to a special geometrical transform. In the present paper, we obtain explicit formulas for 𝜈(𝑟;𝐷, 𝑐0) for the cases 𝐷 = 3 and 𝑐0 = 1, 2. Thus this and previous author’s papers cover the case 𝐷 = 3.
The initial boundary value problems solution for the heat equation is represented as a decomposition into a series of Hermite polynomials. For the Cauchy problem and the Cauchy retrospective problem, the coefficients of the solution expansion into series by Hermite polynomials are found. The relationship between the Laplace transform and the Hermite polynomial series is investigated. A new formula for inverting the integral Laplace transform with respect to the values of the image on the real half- axis is found. The original function is constructed as the sum of a quasi-series. A formula is obtained for the Laplace representation as the sum of a quasi-minor series.The problem of reconstructing the temperature field of an unlimited rod based on its moments has been solved.
The paper defines a uniform distribution in a unit 𝑠-dimensional cube of a sequence of nested generalized parallelepiped grids of type II with a weight function. In addition, a definition of a uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of 𝑀𝑛 grids with a weight
function is given.
A proof is given of an analogue of the generalized G. Weyl criterion on necessary and sufficient conditions for a uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of 𝑀𝑛 grids with weights.
Since the definition of the uniform distribution of a sequence of nested generalized parallelepiped grids of type II with a weight function differs from the definition of the uniform distribution of a sequence of grids 𝑀𝑛 with a weight function, the paper proves the second analogue of the Weyl criterion on the necessary and sufficient conditions for the uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of nested generalized parallelepiped grids of type II.
The following theorem is proved:
Theorem 2. Let the Fourier series of 𝑓(⃗𝑥) converge absolutely, 𝐶(⃗𝑚) be its Fourier coefficients and 𝑆𝑀,⃗𝜌(⃗𝑚) be the trigonometric sums of the weighted grid, then the following equality holds
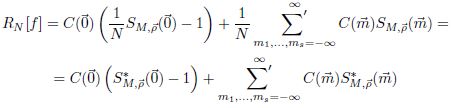
and as 𝑁 → ∞ the error 𝑅𝑁[𝑓] will tend to zero if and only if the weighted nodes of the quadrature formula are uniformly distributed in the unit 𝑠–dimensional cube.
Using the second moment of Dirichlet 𝐿-functions on the critical line over the major arcs M(L𝑏), with 𝜏 = 𝑦3𝑥−1L−𝑏1 , and excluding a small neighborhood of the centers of these arcs, i.e., those 𝛼 satisfying |𝛼 − 𝑎
𝑞 | > (8𝜋𝑦2)−1, for 𝑦 ⩾ 𝑥^1− 1/(9−4√2)L𝑐2 , where 𝑐2 = 2𝐴+24+(√2−1)𝑏1/2√2−1, we obtain the estimate
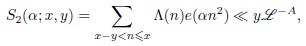
Moreover, in a small neighborhood of the center of the major arcs, defined by |𝛼−𝑎𝑞 | ⩽ (8𝜋𝑦2)−1,for 𝑦 ⩾ 𝑥^5/8 L1,5𝐴+0,25𝑏+18, an asymptotic formula with a remainder term is obtained for 𝑆2(𝛼; 𝑥, 𝑦), where 𝐴, 𝑏1, and 𝑏 are arbitrary fixed positive constants, and L = ln 𝑥.
For sufficiently large integers 𝐾, 𝑥, 𝑦, 𝑞, subject to 𝐾 ⩽ 𝑦 < 𝑥, 𝑛 — fixed natural number, 𝛼 — real, |𝛼 − 𝑎/𝑞|⩽ 1/𝑞^2 , (𝑎, 𝑞) = 1, 𝑞 ⩾ 1, an estimate of the form
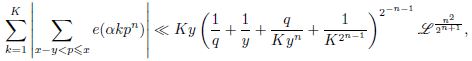
which is a strengthening and generalization of I. M. Vinogradov’s theorem on the distribution of fractional parts of {𝛼𝑝}.
The paper is devoted to abelian groups containing at least one endomorphism whose kernel coincides with its image. Note that the condition ker𝜙 = Im 𝜙 implies the equality 𝜙^2 = 0, that is, 𝜙 is a nilpotent endomorphism of nilpotency index 2.
The main technical result of the paper is Theorem 1, in which a criterion for the existence of an endomorphism of an abelian group whose kernel coincides with its image is obtained in the language of subgroups.
In this paper, the existence of an endomorphism whose kernel coincides with its image is completely solved for Abelian groups from the classes of cyclic and cocyclic groups, elementary 𝑝-primary Abelian groups, and finitely generated Abelian groups.
The main result of the paper is Theorem 12, which proves that a finitely generated Abelian group 𝐴 has an endomorphism whose image coincides with its kernel if and only if either 𝐴 is a finite group whose order is a perfect square, or 𝐴 = 𝐹 ⊕ 𝐾, where 𝐹 is a free Abelian group
of even rank and 𝐾 is an arbitrary finite Abelian group.
This paper introduces the concept of the Fibonacci Word Index FWI, a novel topological index derived from the Albertson index, applied to trees constructed from Fibonacci words.
Building upon the classical Fibonacci sequence and its generalizations, we explore the structural properties of Fibonacci word trees and their degree-based irregularity measures. We define the FWI and its variants, including the total irregularity and modified Fibonacci Word Index where it defined as
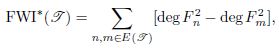
and establish foundational inequalities relating these indices to the maximum degree of the underlying trees. Our results extend known graph invariants to the combinatorial setting of Fibonacci words, providing new insights into their algebraic and topological characteristics. Additionally, we present analytical expressions involving Fibonacci numbers and their generating functions, supported by Binet’s formula, to facilitate computation of these indices. The theoretical developments are illustrated with examples, including detailed constructions of Fibonacci word trees and their degree distributions. This work opens avenues for further investigation of word-based graph invariants and their applications in combinatorics and theoretical computer science.
In our paper we study Albertson Index and Sigma index in Trees Given by Degree Sequences and introduced the irregularity of Albertson Index and Sigma index for sequences of degree(2,3,4), We supported this with a set of illustrative examples of obtaining the general relationship as:
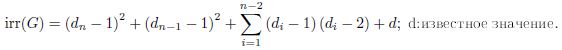
Сomputer science
The work is devoted to the history of the relationship between mathematics and its applications in the humanities, in this case with economic sciences, linguistics, literary criticism, history. It is generally recognized that the role of mathematics in the humanities, where man
is invariably present with his emotions, preferences, moods and other manifestations of the human spirit, can be useful in the computational and statistical aspects. The main question is how productive can the role of mathematics be, can we expect fundamentally new results from
mathematical methods? Consideration of the impact of mathematics on various humanities convinces us of a positive answer to this question. The extent of the application of mathematics is extremely broad: from the accuracy and clarity of the conceptual apparatus, the penetration of the "mathematical spirit"to solving problems according to the standards of rigor and logical precision adopted in mathematics itself, from quantitative methods to qualitative models.
The article considers the current problem of integrating artificial intelligence technologies into the educational process, in particular, in the study of mathematical disciplines. Based on the analysis of scientific research, the authors come to the conclusion that in the context of the transformation of education, intelligent technologies are actively introduced into the educational process, and the growing interest in their use in teaching is confirmed by the statistics of the Yandex.Wordstat tool. Analysis of solutions to a mathematical problem by various generative systems showed that universal models (ChatGPT, GigaChat, YandexGPT) often make logical and computational errors, while specialized systems (MathGPT, Mathos AI, Photomath) demonstrate high accuracy of solutions. Based on the analysis data, the authors emphasize the need to develop critical thinking and digital literacy skills in students. In order to develop these qualities, some methodological approaches are proposed: comparative analysis
of solutions, discussions about the limits of trust in artificial intelligence, deliberate use of erroneous answers from artificial intelligence services as educational material. The authors also address the ethical issues of using artificial intelligence technologies as an auxiliary tool rather
than a source of ready-made solutions.
The problem of diffraction of a plane sound pressure pulse by an infinite solid circular multilayer cylinder consisting of an arbitrary number of homogeneous isotropic elastic coaxial cylindrical layers of different thicknesses is considered. The pulse, propagating in an ideal fluid, falls on the cylindrical body parallel to its generatrix. The sound pressure in the wave scattered by the body is determined.
The components of displacement vector and stress tenzor in each homogeneous element of the multilayer body are expressed through the scalar and vector potentials of elastic displacements.
The sought pressure in the fluid, the scalar potential and the only non-zero component of the vector potential of elastic displacements satisfy the wave equations. Their solutions are found for zero initial conditions, conditions of free slip on the surface of the body in contact with the
fluid, conditions of rigid adhesion on the surfaces separating homogeneous elements of the body, the condition of attenuation of the scattered sound wave and the condition of boundedness of
the wave field in the cylinder.
The integral Laplace transform with respect to time is used to solve the problem. In the image space, the sought pressure and potentials are represented as expansions in series in cylindrical basis solutions of the Helmholtz equation, taking into account the conditions of radiation
at infinity and boundedness. The unknown coefficients included in the series are determined from a system of linear algebraic equations written for each summation index and obtained by substituting the images of the solutions into the images of the boundary conditions. The transition to the space of originals is carried out numerically. Using the previously obtained solution by the authors to the problem of scattering a plane acoustic pressure pulse by a homogeneous elastic cylinder with a continuously inhomogeneous elastic coating, the possibility of mathematical modeling of such a coating by a multilayer coating in a non-stationary problem of sound diffraction is shown.
The problem of plane acoustic wave scattering on an isotropic, linear-elastic body represented by an unstructured polygonal mesh is considered. The problem is studied in the context of acoustics and elastodynamics. An efficient algorithm based on the boundary element method (BEM) and collocation is proposed for computing the scattered wave potential. The main implementation challenges include the non-uniqueness of the boundary acoustic equation, the singularity of integrals, and the full population of the system matrix. To overcome these issues, the Burton – Miller combined equation, regularization using Green’s function identities, and Voronoi-based mesh partitioning are employed. Compared to the finite element method (FEM),
the proposed approach reduces computational costs as it requires discretization of the object’s surface only. The developed method is validated by comparing it with the analytical solution for a sphere and with numerical solutions for complex bodies obtained using COMSOL. The results show that the proposed algorithm effectively computes acoustic fields for isotropic objects of arbitrary shape represented by polygonal meshes.
Due to the increase in the average age of the country’s population, there is a growing need for joint replacement, restoration of the musculoskeletal system and in the field of dentistry.
The main treatment for these diseases involves the use of implants to replace or strengthen the affected bone tissue. Metal materials are the most in demand due to the combination of high mechanical properties and corrosion resistance. The effectiveness of using implants depends
on several factors – biochemical, biomechanical, and histological compatibility. Biomechanical compatibility is determined by the correspondence of the elastic modules of the bone tissue and the implanted structure. Titanium nickelide, TiNi, which has the lowest Young’s modulus, stands out among the new metal alloys for implantation. The creation of porous materials can further bring the values of the elastic constants of the implant material and bone tissue closer and, in addition, ensure good integration of the implant with bone structures. It is proposed to use powder metallurgy methods to create porous titanium nickelide. TiNi powder obtained by calcium hydride reduction is sintered according to different temperature and time regimes - temperatures ranged from 900 to 1290 °C, duration - from 10 to 360 min. 24 sintering modes were implemented and samples with different porosities were obtained. Statistical processing of the obtained results showed that the sintering duration factor has no effect in the studied time range. The dependence of porosity on the sintering temperature is described by an exponential equation. It is shown that the porosity varies slightly up to temperatures of 1200 °C, and at higher sintering temperatures it sharply decreases to minimum values. The results of the study showed that obtaining TiNi samples with different porosities will require precise compliance with the sintering temperature regime. In this case, the time factor does not play a significant role in the change in porosity.
This article is dedicated to the 110th anniversary of the birth of the outstanding world — famous mathematician Academician Yu. V. Linnik and his discrete ergodic method. First, biographical information about Yu. V. Linnik is given. Then, after a brief presentation of the necessary information from the arithmetic of quaternions including the theory of quaternion rotations constructed by B. A. Venkov, the very idea of the discrete ergodic method (hereinafter DEM), belonging to Yu. V. Linnik, is considered.
The next part of the article is devoted to the presentation of the ergodic theorem in the case of quaternions and its application to the question of the asymptotics of integer points over regions on a sphere with increasing radius.
After this applications of the DEM to indefinite ternary quadratic forms corresponding to cases of integer point distributions on hyperboloids, using second-order matrix arithmetic instead of quaternions.
The article concludes with a statement of some unsolved problems related of DEM and a list of references.
In paper the problem of reflecting a plane harmonic sound wave from a flat surface having a cylindrical protrusion is considered. It is assumed that the flat surface and the surface of the projection are absolutely rigid. An incident plane sound wave propagates perpendicular to the
generatrix of a cylindrical projection in a half-space filled with a homogeneous ideal compressible liquid.
An analytical solution of the problem is obtained by the integral method of least squares.
The solution is sought in the form of a truncated row by wave cylindrical functions. To fulfill the boundary conditions on a flat surface and a cylindrical projection the functional is constructed and an approximate solution minimizing its is found.
The results of numerical calculations of the directional patterns of the reflected acoustic field in the far zone are presented.
Краткие сообщения
This work is devoted to the study of a class of cellular automata. An automaton describes evolution on a discrete plane. Transition rules to the next state are specified. Standard questions for such evolutionary automata are investigated, including the existence of immortal
configurations and of periodic evolutions.
A criterion is found for the transition rules under which an immortal configuration exists.
It is shown that in the case of symmetric templates, periodic evolutions can have only period 2.
In perspective, a more detailed description of the various possible evolutions generated by a given fixed set of rules (template) is possible.
Estimates of a polynomial in a Lacunar series with 𝑞-basis coefficients are given.
The article describes the directions of research on the arithmetic properties of series values of the form
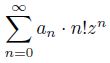
with coefficients 𝑎𝑛 satisfying certain conditions. Under these conditions, the considered series, other than the polynomial, converges in the field C only at 𝑧 = 0. However, for almost all but a finite number of primes, such a series converges in the fields Q𝑝. Therefore there are two ways of research. We can either consider the arithmetic properties of the result of some summation of this series, or consider the values of this series in the field Q𝑝. The paper formulates conjectures, related to the values of the considered series.






























