Сумма коротких тригонометрических сумм с простыми числами
https://doi.org/10.22405/2226-8383-2025-26-3-235-246
Аннотация
Для достаточно больших целых чисел 𝐾, 𝑥, 𝑦, 𝑞 при условии 𝐾 ⩽ 𝑦 < 𝑥, 𝑛 — фиксированное натуральное число, 𝛼 — вещественное,
⃒𝛼 − 𝑎/𝑞|⩽ 1/𝑞2 , (𝑎, 𝑞) = 1, 𝑞 ⩾ 1, получена оценка вида
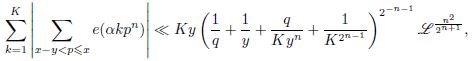
что является усилением и обобщением теоремы И. М. Виноградова о распределении дробных частей {𝛼𝑝}.
Об авторе
Фируз Заруллоевич Рахмонов
Институт математики им. А. Джураева НАН Таджикистана
Россия
Россия
кандидат физико-математических наук
Список литературы
1. Виноградов И. М. Избранные труды — М: Изд-во АН СССР, 1952 г.
2. Виноградов И. М., Карацуба А. А. Метод тригонометрических сумм в теории чисел // Труды МИАН СССР. 1984. Т. 77. С. 4 – 30.
3. Рахмонов З. Х. Теорема о среднем значении 𝜓(𝑥, 𝜒) и ее приложения // Известия РАН. Сер. матем. 1993. Т. 57, № 4. С. 55 – 71.
4. Рахмонов Ф З. Оценка квадратичных тригонометрических с простыми числами // Вестник Московского университета. Серия 1: Математика. Механика. 2011. № 3. С. 56 – 60.
5. Рахмонов З. Х., Рахмонов Ф. З. Сумма коротких тригонометрических сумм с простыми числами // Доклады Академии наук. 2014. Т. 459, № 2. С. 156 – 157.
6. Рахмонов З.Х., Рахмонов Ф.З., Исматов С.Н. // Оценка сумм коротких тригонометрических сумм с простыми числами //Доклады Академии наук Республики Таджикистан. 2013. Т. 56. № 12. С. 937 – 945.
7. Рахмонов З. Х., Рахмонов Ф З. Асимптотическая формула в проблеме Варинга с почти пропорциональными слагаемыми // Чебышевский сборник. 2024. Т. 25. № 2(93). С. 139-168.
8. Рахмонов Ф З. Асимптотическая формула в обобщении тернарной проблемы Эстермана с почти пропорциональными слагаемыми // Чебышевский сборник. 2024. Т. 25. № 4(95). С. 120–137.
9. Рахмонов Ф З. Оценка коротких тригонометрических сумм Г. Вейля в малых дугах // Доклады Национальной академии наук Таджикистана. 2024. Т. 67. № 5-6. С. 238-242.
10. Рахмонов З.Х., Рахмонов Ф.З. Проблема Варинга с почти пропорциональными слагаемыми // Доклады Национальной академии наук Таджикистана. 2023. Т. 66. № 9-10. С. 481-488.
11. Рахмонов З.Х., Рахмонов Ф.З. Асимптотическая формула в проблеме Варинга с почти пропорциональными слагаемыми // Доклады Национальной академии наук Таджикистана. 2024. Т. 67. № 3-4. С. 125-136.
12. Вон Р. Метод Харди–Литтлвуда — Москва: Мир, 1985.
13. Рахмонов Ф.З. Оценка тригонометрических сумм с простыми числами // Чебышевский сборник. 2011. Т. 12. В. 1. С. 158–171.
14. Рахмонов Ф.З. Оценка квадратичных тригонометрических сумм с простыми числами // Вестник Московского университета. Серия 1. Математика и механика. 2011. № 3. С. 56–60.
15. Рахмонов З. Х., Рахмонов Ф. З. Короткие кубические суммы простыми числами // Труды Математического института им. В. А. Стеклова Российской академии наук. 2016. Т. 296. С. 220-242.
16. Рахмонов З. Х., Рахмонов Ф З. Тригонометрические суммы с функцией Мёбиуса // Чебышевский сборник. 2019. Т. 20. № 4. С. 281-305.
17. Архипов Г. И., Чубариков В. Н. Три теоремы о тригонометрических суммах из анализа // Доклады Российской Академии наук. 1994. Т. 335. № 4. С. 407–408.
18. Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по математическому анализу // Москва: Дрофа. 2004. 635с.
19. Марджанишвили К.К. Оценка одной арифметической суммы // ДАН СССР. 1939. Т. 22. № 7. С. 391-393.
20. Карацуба А. А. Основы аналитической теории чисел — М.: Наука, 1983, 2-ое изд. 21. Heath-Brown D. R. The number of primes in a short interval // Journal f¨ur die reine und angewandte Mathematik. 1988. V. 389. P. 22-63.
Рецензия
Для цитирования:
Рахмонов Ф.З. Сумма коротких тригонометрических сумм с простыми числами. Чебышевский сборник. 2025;26(3):235-246. https://doi.org/10.22405/2226-8383-2025-26-3-235-246
For citation:
Rakhmonov F.Z. Sum of short exponential sums with prime numbers. Chebyshevskii Sbornik. 2025;26(3):235-246. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-235-246
Просмотров:
1
Послать статью по эл. почте 