Индекс Альбертсона и индекс Сигмы в деревьях, заданных последовательностями степеней
https://doi.org/10.22405/2226-8383-2025-26-3-274-283
Аннотация
В нашей статье мы изучаем индекс Альбертсона и сигма-индекс в деревьях, заданных степенными последовательностями, и ввели нерегулярность индекса Альбертсона и сигма-индекса для последовательностей степени(2,3,4), подкрепив это набором иллюстративных примеров получения общего соотношения в виде:
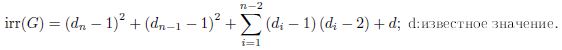
Об авторах
Жасем Хамуд
Московский физико-технический институт (Национальный исследовательский университет)
Россия
Россия
аспирант
Дуаа Абдулла
Московский физико-технический институт (Национальный исследовательский университет)
Россия
Россия
аспирант
Список литературы
1. Ли На, Чжоу Б., Мяо Б. Общий индекс неравномерности Альбертсона для графов // Математика AIMS. — 2024. — Т. 7, № 1. — С. 267–282. — DOI: 10.3934/math.2022002.
2. Хейнс Т. В., Хедетниеми С. Т., Слейтер П. Дж. Основы доминирования в графах. — Нью-Йорк: Marcel Dekker, Inc., 1998. — 446 с.
3. Доржсембе С., Буянтогтох Л., Гутман И., Хоролдагва Б., Рети Т. Неравномерность графов // Журнал коммуникаций в математической и компьютерной химии. — 2023. — Т. 89. — С. 371–388. — DOI: 10.46793/match.89-2.371D.
4. Али А., Димитров Д., Рети Т., Альбалахи А. М., Хамза А. Е. Оценки и оптимальные результаты для меры полной неравномерности // arXiv [Электронный ресурс]. — 2025. — DOI: 10.48550/arXiv.2501.01538.
5. Гутман И., Кулли В. Р., Реджепович И. Индекс неравномерности Сомбор // Бюллетень Академии сербских наук и искусств. — 2023. — Т. 156. — С. 31–37.
6. Галаванд А., Ашрафи А., Димитров Д. О неравномерности графов на основе неравенства средних арифметического и геометрического // Математические неравенства и приложения. — 2023. — Т. 26, № 1. — С. 151–160. — DOI: 10.7153/mia-2023-26-12.
7. Абдо Х., Димитров Д., Гутман И. Неравномерность графа и её меры // Прикладная математика и вычисления. — 2019. — Т. 357. — С. 317–324. — DOI: 10.1016/j.amc.2019.04.013.
8. Мандал Й. С., Прванович М. Обратная задача для индекса неравномерности Альбертсона // Журнал алгебраической инженерной математики. — 2022. — Т. 12, № 3. — С. 1–10.
9. Гутман И., Руссич Б., Тринаистич Н., Уилкокс К. Ф. Теория графов и молекулярные орбитали. XII. Ациклические полиены // Журнал химической физики. — 1975. — Т. 62, № 9. — С. 3399–3405.
10. Гутман И., Тоган М., Юртташ А., Джевик А. С., Джангул И. Н. Обратная задача для сигма-индекса // Сообщения по математике и компьютерной химии MATCH. — 2016. — Т. 79, № 2. — С. 491–508.
11. Гутман И., Тринаистич Н. Теория графов и молекулярные орбитали. Полная 𝜋-электронная энергия альтернантных углеводородов // Письма по химической физике. — 1972. — Т. 17, № 4. — С. 535–538.
12. Галаванд А., Гутман И., Таваколи М., Бесси С., Гонсалвес Д., Рейнальд А. Мера неравномерности графов // Журнал математики. — 2023. — Т. 2023. — DOI: 10.1155/2023/4891183.
13. Сюй Кэсян. Деревья с семью наименьшими и восемью наибольшими индексами Харари // Дискретная прикладная математика. — 2012. — Т. 160, № 3. — С. 321–331. — DOI: 10.1016/j.dam.2011.08.014.
14. Николич С., Ковачевич Г., Миличевич А., Тринаистич Н. Zagreb-индексы 30 лет спустя // Хорватский химический Acta. — 2003. — Т. 76, № 2. — С. 113–124.
15. Альбертсон М. О. Неравномерность графа // Ars Combinatoria (Искусство комбинаторики). — 1997. — Т. 46. — С. 219–226.
16. Гутман И., Хансен П., Мело Х. Поиск с переменным окрестностью для экстремальных графов. 10. Сравнение индексов неравномерности для химических деревьев // Журнал химической информации и моделирования. — 2005. — Т. 45, № 2. — С. 222–230.
17. Абдо Х., Брандт С., Димитров Д. Полная неравномерность графа // Дискретная математика и теоретическая информатика. — 2014. — Т. 16 (Теория графов). — С. 201–206.
Рецензия
Для цитирования:
Хамуд Ж., Абдулла Д. Индекс Альбертсона и индекс Сигмы в деревьях, заданных последовательностями степеней. Чебышевский сборник. 2025;26(3):274-283. https://doi.org/10.22405/2226-8383-2025-26-3-274-283
For citation:
Hamoud J., Abdullah D. Albertson index and Sigma index in trees given by degree sequences. Chebyshevskii Sbornik. 2025;26(3):274-283. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-274-283
Просмотров:
22
Послать статью по эл. почте 