Арифметические свойства значений расходящихся в поле C рядов. Гипотезы
https://doi.org/10.22405/2226-8383-2025-26-3-300-306
Аннотация
Статья продолжает описание направлений исследования арифметических свойств значений рядов вида
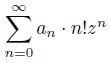
с коэффициентами 𝑎𝑛, удовлетворяющими определённым условиям. При этих условиях рассматриваемый ряд, отличный от многочлена, сходится в поле C только при 𝑧 = 0.
Однако для почти всех, кроме конечного числа, простых чисел 𝑝 такой ряд сходится в полях Q𝑝. Поэтому есть два естественных пути исследования. Мы можем рассматривать либо значения результата некоторого суммирования этого ряда, либо его значения в поле
Q𝑝. В статье формулируются гипотезы, относящиеся к значениям рассматриваемых рядов как в одном, так и в другом случае.
Об авторе
Владимир Григорьевич Чирский
Московский государственный университет им. М. В. Ломоносова; Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации
Россия
Россия
доктор физико-математических наук
Список литературы
1. Чирский В. Г. Арифметические свойства значений расходящихся в поле 𝐶 рядов // Чебышевский сборник.-2024.-т. 25.- вып. 3.-с. 259 – 269.
2. Шидловский А. Б. Трансцендентные числа.-М.: «Наука».-1987.-448 с.(Английский перевод:[3] Andrei B.Shidlovskii. Transcendental Numbers. W.de Gruyter.-Berlin.-New York.-1989.-467pp.).
3. Харди Г. Г. Расходящиеся ряды.-М.:«URSS».-2006.-506с.
4. Рамис Ж.П. Расходящиеся ряды и асимптотические теории.-М.-Иж.: «Институт компьютерных технологий».-2002.-80 с.
5. Ferguson T. Algebraic properties of Э-functions.//J.Number Theory. 2021.- v.229, pp.168-178.
6. Fischler S.;Rivoal T. Arithmetic theory of E-operators .//J.d l’Ecole polytechnique-Mathematiques.-2016.-т. 3.-с. 31 -65
7. Fischler S.;Rivoal T. Microsolutions of differential operators and values of arithmetic Gevrey series.//Michigan Math. J.-2018.-c.239-254
8. Rivoal T.On the arithmetic nature of the values of the Gamma function,Euler’s constant and Gompertz’s constant.//American J.of Math.-2012.-n/140.-№2.-с.317-348.
9. Fischler S.;Rivoal T. Relations between values of arithmetic Gevrey series, and applications to values of the Gamma function. arXiv:2301.13518v1[math.NT].
10. Andre Y.Arithmetic Gevrey series and transcendence. A survey.//J.Theor.Nombres Bordeaux.-2003.-т.15.-с.1-10.
11. Bertrand D.;Beukers F.Equations differentielles linearies et majorations de multiplicities.-1985.- Annales scientifiques ENS.-т.18.-№1.-с.181-192.
12. Chirskii V. G. Product Formula, Global Relations and Polyadic Integers // Russ. J. Math. Phys. 2019.- v.26, no.3, pp.286-305.
13. Chirskii V. G. Arithmetic properties of generalized hypergeometric 𝐹– series // Russ. J. Math. Phys. 2020.- v.27, no.2, pp.175-184.
14. Ernvall-Hytonen A.-M.;Matala-aho T.;Seppala I. Euler’s factorial series, Hardy integral, and continued fractions // J.Number Theory. 2023.-v.244.-pp.224-250.
Рецензия
Для цитирования:
Чирский В.Г. Арифметические свойства значений расходящихся в поле C рядов. Гипотезы. Чебышевский сборник. 2025;26(3):300-306. https://doi.org/10.22405/2226-8383-2025-26-3-300-306
For citation:
Chirskii V.G. Arithmetic properties of values of divergent in C series. Conjectures. Chebyshevskii Sbornik. 2025;26(3):300-306. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-300-306
Просмотров:
2
Послать статью по эл. почте 