Равномерное распределение в единичном кубе взвешенных узлов квадратурной формулы
https://doi.org/10.22405/2226-8383-2025-26-3-185-219
Аннотация
В работе даётся определение равномерного распределения в единичном 𝑠-мерном кубе последовательности вложенных обобщенных параллелепипедальных сеток II типа с весовой функцией. Кроме того, даётся определение равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности сеток 𝑀𝑛 с весовой функцией.
Даётся доказательство аналога обобщённого критерия Г. Вейля об необходимых и достаточных условиях равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности сеток 𝑀𝑛 с весами.
Так как определение равномерного распределения последовательности вложенных обобщенных параллелепипедальных сеток II типа с весовой функцией отличается от определения равномерного распределения последовательности сеток 𝑀𝑛 с весовой функцией, то в работе доказывается второй аналог критерия Вейля о необходимых и достаточных условиях равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности вложенных обобщенных параллелепипедальных сеток II типа.
Доказана следующая теорема:
Теорема 1. Пусть ряд Фурье функции 𝑓(⃗𝑥) сходится абсолютно, 𝐶(⃗𝑚) — ее коэффициенты Фурье и 𝑆𝑀,⃗𝜌(⃗𝑚) — тригонометрические суммы сетки с весами, тогда справедливо равенство
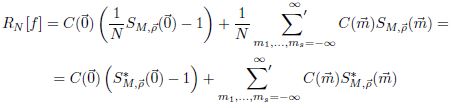
и при 𝑁 → ∞ погрешность 𝑅𝑁[𝑓] будет стремиться к нулю тогда и только тогда, когда взвешенные узлы квадратурной формулы равномерно распределены в единичном 𝑠–мерном
кубе.
Об авторах
Елена Михайловна Рарова
Тульский государственный педагогический университет им. Л. Н. Толстого
Россия
Россия
Николай Николаевич Добровольский
Тульский государственный педагогический университет им. Л. Н. Толстого; Московский государственный университет им. М. В. Ломоносова
Россия
Россия
доктор физико-математических наук
Ирина Юрьевна Реброва
Тульский государственный педагогический университет им. Л. Н. Толстого
Россия
Россия
кандидат физико-математических наук
Ирина Николаевна Балаба
Тульский государственный педагогический университет им. Л. Н. Толстого
Россия
Россия
доктор физико-математических наук, профессор
Список литературы
1. Бабенко, К. И. Основы численного анализа. М.: Наука, 1986.
2. Бахвалов, Н. С. О приближенном вычислении кратных интегралов // Вестн. Моск. ун-та, 1959. № 4. С. 3–18.
3. Бочарова, (Добровольская) Л. П. Алгоритмы поиска оптимальных коэффициентов // Чебышевский сборник 2007 Т. 8, вып. 1(21). Тула, Из-во ТГПУ им. Л. Н. Толстого. С. 4 — 109.
4. Вейль, Г. Алгебраическая теория чисел М.: И*Л, 1947.
5. Герцог, А. С., Ребров, Е. Д., Триколич, Е. В. О методе К. К. Фролова в теории квадратурных формул // Чебышевский сб. — Т. X. Вып. 2(30). — Тула: Изд-во Тул. гос. пед. ун-та им. Л. Н. Толстого, 2009. — С. 10–54.
6. Герцог, А. С. Численное вычисление четырехкратных интегралов по методу Фролова с использованием алгебраических сеток биквадратичного поля Дирихле Q(√2 +√3) // Известия Тульского государственного университета. Естественные науки. Вып. 3. — Тула: Изд-во ТулГУ, 2011. — С. 22–30.
7. Герцог, А. С. Параметризация четырехмерной сетки биквадратичного поля Дирихле // Научные ведомости Белгородского государственного университета. Серия: Математика. Физика. №23(188). Вып. 5. Белгород: Изд-во БелГУ, 2011. С. 41–53.
8. Герцог, А. С. ПОИВС ТМК: Биквадратичные поля и квадратурные формулы // Материалы международной научно-практической конференции «Многомасштабное моделирование структур и нанотехнологии», посвященной 190-летию со дня рождения академика Пафнутия Львовича Чебышёва, столетию со дня рождения академика Сергея Васильевича Вонсовского и 80-летию со дня рождения член-корреспондента Виктора Анатольевича Буравихина. Тула: Изд-во Тул. гос. пед. ун-та им. Л. Н. Толстого, 2011. С. 242–247.
9. Добровольская, Л. П., Добровольский Н. М., Добровольский Н. Н., Огородничук Н. К., Ребров Е. Д., Реброва И. Ю. Некоторые вопросы теоретико-числового метода в приближенном анализе // Труды X международной конференции «Алгебра и теория чисел: современные проблемы и приложения».- Ученые записки Орловского государственного университета. 2012. № 6. Часть 2. С. 90 – 98.
10. Добровольская, Л. П., Добровольский М. Н. , Добровольский Н. М., Добровольский Н. Н. Гиперболические дзета-функции сеток и решёток и вычисление оптимальных коэффициентов // Чебышевский сборник 2012 Т. 13. Вып. 4(44). Тула, Из-во ТГПУ им. Л. Н. Толстого. С. 4 – 107.
11. Добровольская, Л. П., Добровольский, Н. М., Симонов, А. С. О погрешности приближенного интегрирования по модифицированным сеткам // Чебышевский сборник.- 2008.- Т. 9.- вып. 1(25).- Тула, Из-во ТГПУ им. Л. Н. Толстого. С. 185 – 223.
12. Добровольский, Н. М. Оценки отклонений обобщенных параллелепипедальных сеток. Деп. в ВИНИТИ 24.08.84. № 6089–84.
13. Добровольский, Н. М. Гиперболическая дзета функция решёток. Деп. в ВИНИТИ 24.08.84. № 6090–84.
14. Добровольский, Н. М. О квадратурных формулах на классах 𝐸𝛼 𝑠 (𝑐) и 𝐻𝛼 𝑠 (𝑐). Деп. в ВИНИТИ 24.08.84. № 6091–84.
15. Добровольский, Н. М. Теоретико–числовые сетки и их приложения. Дис. ... канд. физ.– мат. наук. Тула, 1984.
16. Добровольский, Н. М. Теоретико–числовые сетки и их приложения. Автореф. дис. ... канд. физ.–мат. наук. Москва, 1985.
17. Добровольский, Н. М. Теоретико–числовые сетки и их приложения // Теория чисел и ее приложения: Тез. докл. Всесоюз. конф. Тбилиси, 1985. C. 67–70.
18. Добровольский, Н. Н. О двух асимптотических формулах в теории гиперболической дзета-функции решёток // Чебышевcкий сборник. 2018. Т. 26, вып. 3, С. 109–134.
19. Коробов, Н. М. Вычисление кратных интегралов методом оптимальных коэффициентов // Вестн. Моск. ун-та, 1959. № 4. С. 19 — 25.
20. Коробов, Н. М. О приближенном вычислении кратных интегралов // ДАН СССР. 1959. Т. 124, № 6. С. 1207 – 1210.
21. Коробов, Н. М. Свойства и вычисление оптимальных коэффициентов // ДАН СССР. 1960. Т. 132. № 5. С. 1009–1012.
22. Коробов, Н. М. Теоретико-числовые методы в приближенном анализе // М.: Физматгиз, 1963.
23. Коробов, Н. М. Тригонометрические суммы и их приложения // М.: Наука.- 1989.
24. Коробов, Н. М. Теоретико-числовые методы в приближенном анализе. (второе издание) // М.: МЦНМО, 2004.
25. Курош, А. Г. Курс высшей алгебры // М: Физматгиз.- 1963.- 432 с.
26. Локуциевский, О. В., Гавриков, М. Б. Начала численного анализа // М.: ТОО Янус.- 1995.
27. Огородничук, Н. К, Ребров, Е. Д. Об алгоритме численного интегрирования с правилом остановки // Материалы 7 международной конференции «Алгебра и теория чисел: современные проблемы и приложения». 2010. Тула, Из-во ТГПУ им. Л. Н. Толстого. С. 153 – 158.
28. Огородничук, Н. К, Ребров, Е. Д. ПОИВС ТМК: Алгоритмы интегрирования с правилом остановки // Международной научно-практической конференции «Многомасштабное моделирование структур и нанотехнологии, посвященной 190-летию со дня рождения академика Пафнутия Львовича Чебышёва, столетию со дня рождения академика Сергея Васильевича Вонсовского и 80-летию со дня рождения член-корреспондента Виктора Анатольевича Буравихина». Тула. Из-во ТГПУ им. Л. Н. Толстого. 2011. С. 153 — 158.
29. Рарова, Е. М. Разложение тригонометрической суммы сетки с весами в ряд по точкам решетки // Изв. ТулГУ. Естественные науки. 2014. Вып. 1. Ч. 1. С. 37–49.
30. Рарова, Е. М. Тригонометрические суммы сетки с весами для целочисленной решётки // Известия Тульского государственного университета. Естественные науки. 2014. № 3. С. 34–39.
31. Рарова, Е. М. Тригонометрические суммы алгебраических сеток // В сборнике: Алгебра, теория чисел и дискретная геометрия: современные проблемы и приложения Материалы XIII Международной конференции, посвященной восьмидесятипятилетию со дня рождения профессора Сергея Сергеевича Рышкова. Тульский государственный педагогичекий университет им. Л. Н. Толстого. 2015. С. 356–359.
32. Рарова, Е. М. О взвешенном числе точек алгебраической сетки // Чебышевcкий сборник, 2018, т. 19, вып. 1, с. 200–219.
33. Рарова, Е. М. Тригонометрические суммы сеток алгебраических решеток // Чебышевcкий сборник, 2019, т. 20, вып. 2, с. 399—405.
34. Рарова, Е. М., Добровольский, Н. Н., Реброва, И. Ю. Асимптотическая оценка для тригонометрических сумм алгебраических сеток // Чебышевcкий сборник.- 2020.- т. 21.- вып. 3.- с. 232—240.
35. Рарова, Е. М., Добровольский, Н. Н., Реброва, И. Ю., Добровольский, Н. М. Тригонометрические суммы сеток алгебраических решеток с бесконечно дифференцируемыми весами // Чебышевcкий сборник. 2021. Т. 22, вып. 3, С. 166–178.
36. Ребров, Е. Д. Алгоритм Добровольской и численное интегрирование с правилом остановки // Чебышевский сборник 2009 Т. 10, вып. 1(29). Тула, Из-во ТГПУ им. Л. Н. Толстого. С. 65–77.
37. Ребров, Е. Д. Квадратурные формулы с модифицированными алгебраическими сетками // Чебышевский сборник 2012 Т. 13, вып. 3(43). С. 53–90.
38. Реброва, И. Ю., Добровольский, Н. М., Добровольский, Н. Н., Балаба, И. Н., Есаян, А. Р., Басалов, Ю. А. Теоретико-числовой метод в приближённом анализе и его реализация в ПОИВС «ТМК»: Моногр. В 2 ч. Под. ред. Н. М. Добровольского. — Тула: Изд-во Тул. гос. пед. ун-та им. Л. Н. Толстого, 2016. - Ч. I. - 232 с.
39. Фролов, К. К. Оценки сверху погрешности квадратурных формул на классах функций // ДАН СССР. 231. 1976. № 4. С. 818–821.
40. Фролов, К. К. Квадратурные формулы на классах функций. Дис. ... канд. физ.-мат. наук. М.: ВЦ АН СССР. 1979.
41. Nikolay M. Dobrovolskiy, Larisa P. Dobrovolskaya, Nikolay N. Dobrovolskiy, Nadegda K. Ogorodnichuk, and Evgenii D. Rebrov Algorithms fot computing optimal coefficients // Book of abstracts of the International scientific conference "Computer Algebra and Information Technology" , Odessa, August 20—26, 2012. p. 22 — 24.
Рецензия
Для цитирования:
Рарова Е.М., Добровольский Н.Н., Реброва И.Ю., Балаба И.Н. Равномерное распределение в единичном кубе взвешенных узлов квадратурной формулы. Чебышевский сборник. 2025;26(3):185-219. https://doi.org/10.22405/2226-8383-2025-26-3-185-219
For citation:
Rarova E.M., Dobrovol’skii N.N., Rebrova I.Yu., Balaba I.N. Uniform distribution in the unit cube of weighted nodes of the quadrature formula. Chebyshevskii Sbornik. 2025;26(3):185-219. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-185-219
Просмотров:
1
Послать статью по эл. почте 