Let $X-$be a sufficiently large real number, $b_{1},b_{2},b_{3}-$be integers with the condition $1\le {{b}_{1}},{{b}_{2}},{{b}_{3}}\le X,\,\,\, a_{ij}, (i=1,2,3;\,\,\, j=\overline{1.5})$  positive integers, $p_{1},...,p_{5}-$prime numbers. Let us set $B=max\{3|a_{ij}|\} ,\,\,(i=1,2,3;\,\,j=\overline{1.5}), \vec{b} = (b_{1},b_{2},b_{3}),\,\, K=36\sqrt{3}B^{5}|\vec{b}|, E_{3,5}(X)=\\=card\{b_{i} |1\le {{b}_{i}}\le X,\,\,b_{i}\neq a_{i1} p_{1}+\cdots+a_{i5} p_{5},\,\,i=1,2,3\}$. In the paper it is proved that the system $b_{i}=a_{i1}p_{1}+\cdots+a_{i5}p_{5},\,\,(i=1,2,3)$ is solvable in prime numbers $p_{1},\cdots,p_{5}$, for all triples $\vec{b}=(b_{1}, b_{2},b_{3}),\,\, 1\le {{b}_{1}},{{b}_{2}},{{b}_{3}}\le X$, with the exception of no more than $E_{3,5}(X)$ triples of them, and a lower bound is obtained for the $R(\vec{b})-$number of solutions of this system, that is, the inequality $R(\vec{b})>> K^{2-\varepsilon}( \log K)^{-5}$ is proved to be true, for all $(b_{1},b_{2},b_{3})$ with the exception of no more than $X^{3-\varepsilon}$ triples of them.

In this article we introduce the concept of strongly star I-compactness and study some of its topological features. We represent some finite intersection like properties for both I-compact spaces and strongly star I-compact spaces. Lastly we establish a relation between the countably 𝐼𝑓𝑖𝑛-compact space and the strongly star 𝐼𝑓𝑖𝑛-compact space. In order to identify the difference between the different versions of compactness we represent some counter examples. And some open problems are also posed in this article.

The system is in critical condition if even a small disturbance can lead to global changes.
These are, for example, any phase transitions: in water cooled to zero degrees, one crystallization
center rapidly grows to a large cluster. The concept of self-organizing criticality was first proposed by Back, Tang and Weisenfeld in 1987. In their work, they described a system that has become a classic model of self-organizing criticality: on a square grid, in some nodes, there are grains of sand, a finite number in total. If there are more than three grains of sand in one of the nodes, a toppling occurs: four grains of sand from this node are redistributed to neighboring nodes, this can cause topplings in them, then in their neighbors... Collapses will occur in an
avalanche-like manner until the system returns to an equilibrium state, this process is called relaxation.
This article presents the results of an experimental and theoretical study of the following problem. Consider a regular graph whose vertices are points in the plane, both coordinates of which are integers, and each vertex is connected to the 8 nearest vertices. Put a large number of grains of sand at the point (0,0) and relax. The relaxation result has an obvious fractal structure, visible in computer experiments, and parts of this structure can be described.
We classify some emerging patterns and propose hypotheses about their structure (based on similar results for other regular graphs). Estimates for the average number of sand in the emerging patterns are proved.

Within the framework of the nonlinear method of angular boundary functions, the existence of solutions to nonlinear boundary value problems is proven through the construction of barrier functions. Barrier functions are constructed through specially designated support barriers. The support barriers themselves can also act as barrier functions. In this case, it is necessary to prove the fulfillment of certain inequalities that are of independent functional interest. The study of these inequalities leads to cumbersome calculations. This paper proposes a method that significantly simplifies obtaining results. Possible solutions to inequalities are constructed
in the form of polynomials. The initial stage involves identifying the polynomial of the highest degree of interest. Such a polynomial is called radical. Next, polynomials of lower degrees, called adjacent polynomials, are successively added to the radical polynomial.

In 1872 R. Dedekind constructed the set of real numbers R as a certain extension of the set of rational numbers Q by taking countable order regular cuts. This method was generalized and
applied by G. MacNeille to some ordered mathematical systems. In this article the Dedekind –
MacNeille method is applied to the mathematical system 𝐶 generated by the family 𝐶𝑏(𝑇, 𝒢) of all continuous bounded functions 𝑓 : 𝑇 /R on the Tikhonov topological space (𝑇, 𝒢).
We consider Dedekind extension 𝐶 / / 𝐷(𝐶), and also countably Dedekind extension 𝐶 / / 𝐷0(𝐶) as a closer analogue of the classical extension Q / / R. Functional-factor descriptions of these extensions are given through families of functions uniform with respect to ensembles of subsets of the set 𝑇 having the Stone property and the Stone cozero property.
Characterizations of these extensions are given as some completions of the lattice linear space 𝐶 endowed with some local structure of ideal refinement.
The functional description and characterization of the countable Dedekind extension 𝐶 / /𝐷0(𝐶) turn out to be surprisingly similar with the functional description and characterization of the Riemannian extension 𝐶 / /𝑅𝜇 generated by the factor-family of all functions on the Tikhonov space (𝑇, 𝒢) 𝜇-Riemann integrable with respect to a positive bounded Radon
measure 𝜇.

Ivanov and Tuzhilin stated the problem of one-dimensional Gromov minimal filling of finite metric spaces, where the filling is considered as a weighted connected graph containing the metric space as a subset of its vertex set. They shown that the problem can be always reduced to the case of so-called binary trees — trees whose vertices have degrees 1 and 3 only. Later Eremin obtained a minimax formula for the weight of the minimal filling. Eremin’s formula uses the concept of minimum parametric filling, i.e. the filling with a fixed graph (parameterization or type), and the weight of the minimal parametric filling turns out to be equal to the maximum value of so-called multi-perimeters over all irreducible multi-tours.
Moustaches of a binary tree is a pair of its vertices of degree 1 having a common adjacent vertex. The number of moustaches can measure complexity of binary trees. In this paper the multi-tours of binary trees with 3 moustaches are investigated. A linear recurrent formula is found for the number of such binary trees. For a fixed binary tree a connection is established between the irreducibility of multi-tours and inclusions of multi-tours multi-graphs.
Recently Shcherbakov proved that the multiplicity of an irreducible multi-tour for a binary tree with 3 moustaches does not exceed 2; in this paper the existence of such irreducible multitour for any binary tree with 3 moustaches is proved.
Ivanov and Tuzhilin proposed to calculate the weight of a minimal parametric filling by finding the vertices of a multidimensional polyhedron of feasible variable values of the dual linear programming problem. These their results are based on computer calculations. The technique developed in this paper permits to find all irreducible multi-tours of a binary tree with 6 boundary vertices and 3 moustaches without a computer.

The structure of the Chevalley algebra over a field or ring 𝐾, associated with an indecomposable root system Φ, essentially depends on its nil-triangular subalgebra 𝑁Φ(𝐾). It turned out to be natural for 𝑁Φ(𝐾) to use the faithful enveloping algebra 𝑅, introduced in 2018, which has the same basis as 𝑁Φ(𝐾). It is known that the isomorphism of the Lie rings 𝑁Φ(𝐾) does not depend on the choice of signs of the structure constants 𝑁𝑟,𝑠. However, for
faithful enveloping rings 𝑅 this property is violated. Therefore, the question of describing their automorphisms was extended to finding all non-isomorphic faithful enveloping rings 𝑁Φ(𝐾) of
type 𝐺2 over 𝐾, and only then finding an explicit description of their automorphisms.

In this paper, we study the asymptotic behavior of the discrete spectrum of the Sturm– Liouville operator given on R+ by the expression −𝑦′′ +𝑞(𝑥)𝑦 and the zero boundary condition 𝑦(0) cos 𝛼 + 𝑦′(0) sin 𝛼 = 0, for rapidly growing potentials 𝑞(𝑥). The asymptotics of the eigenvalues of the operator for the classes of potentials are obtained, which characterize the rate of their growth at infinity.

It is well known that the classical Apollonius’s problem to construct a circle tangent to three given circles using a compass and straightedge has finite number of solutions or has no solutions if the given circles are concentric. The so called degenerate cases are also included in the consideration: any of the circles may be a point (a zero-radius circle) or a straght line (a circle of infinite radius).
In this paper we consider the Apollonius problem not for three circles but for only two, with the degenerate cases also considered. We classify all cases of the problem for all possible objects
(points, lines or circles) and for all cases of their mutual arragements on the real coordinate
plane. For every case not only all solutions are provided but also some of their interdependencies
are shown.
The approaches for solutions of the classified cases are based on the notion of locus of the points being equidistant from the given objects and on the equity of distances from the center of the sought tangent circle to each of the given objects.
Unlike the classical Apollonius’s problem the solution always exists, moreover, the number of solutions is infinite.

In approximation theory, the problems of finding an estimate of the best approximation through the structural properties of the approximated function are well known. The work is devoted to such problems in spaces with an asymmetric norm and sign-sensitive weights.

The article discusses the problems associated with the Ramsey — Kass — Koopmans mathematical model of economic growth. An auxiliary system of differential equations is being constructed, for which it is possible to obtain a solution in quadratures. Based on the obtained solution, the upper estimates of the consumption function are found. Using the upper estimates of the consumption function, we find the maximum value of the time interval in which there are solutions to the auxiliary system of differential equations for the considered parameter values.

Under a special initial condition, we show that there is a solution to the Cauchy problem (𝐾(𝑡), 𝐶(𝑡)) on the entire ray 𝑡 ∈ [0;+∞) and both components increase and tend to the values we found.

In this paper, we propose an algorithm for constructing isospectral and partially isospectral
Dirac operators on a finite interval. This algorithm is applied to the process of finding solutions to mixed problems posed for a system of partial differential equations of hyperbolic type with variable coefficients.

Formulas for the coefficients of the expansion into a series of Appel polynomials associated with a differential equation of parabolic type are obtained. It has been established that Appel polynomials are involved in the formulas for the expansion of the solution to the Cauchy problem for equations of parabolic type into a series of derivatives of the fundamental solution.
A new method for solving the Cauchy problem is proposed, the essence of which is to use series
expansion in Appel polynomials. The results generalize the method for solving the heat equation
on the real axis by expanding it into a series of Hermite polynomials. The connection between
the Fourier transform and series in associated Appel polynomials is studied. The issue of using Hermite polynomials for the Laplace transform has been studied.

We construct a field 𝐸 such that there are infinitely many non-isomorphic quaternion 𝐸-algebras with unitary involution and all such algebras are split by any quadratic field extension of 𝐸.

Artin groups are a generalization of known braid groups, in which the problems of words and conjugacy of words are algorithmically solvable. Due to the complexity of solving these problems in the Artin group class, algorithmic problems are considered in its various subclasses.
In 1983 K. Appel and P. Schupp defined the Artin groups extra-large type.
In 2003, V. N. Bezverkhny introduced the Artin group with a tree structure.
Artin groups of extra-large type and Artin groups with tree structure are well studied and most of the algorithmic problems are solved in them, in particular, the algorithmic solvability of the problem of generalized conjugacy of words is proved.
The article deals with generalized tree structures of Artin groups, which are tree products of Artin groups of extra-large type and Artin groups with a tree structure, united by cyclic subgroups corresponding to generatings these groups.
The authors provide a original proof of algorithmic solvability of the problem of generalized conjugacy of words in generalized tree structures of Artin groups. The method of proof uses the approach of G. S. Makanin, applied by him to study the finite generality of the element Normalizer in braid groups. In addition, this paper shows that the centralizer of a finitely generated subgroup in the generalized tree structure of Artin groups is finitely generated and there is an algorithm that writes out its generators.

The article considers the solution of the problem of power conjugacy of words in generalized tree structures of Artin groups by geometric methods based on the study of diagrams over this class of groups having a single-layer structure, as previously shown by the authors. Chart transformations are used, including abbreviations introduced by M. Den and V. N. Bezverkhnim.
The article is a continuation of the consideration of algorithms for solving problems of combinatorial group theory in generalized tree structures of Artin groups, previously the authors proposed algorithms based on a diagram approach to solve conjugacy problems, generalized conjugacy of words, the construction of centralizers of an element and a finitely generated subgroup.
The class of groups considered in the article is a tree product of Artin groups with a tree structure and Artin groups of extra-large type, amalgamated by cyclic subgroups corresponding to the generators of the groups.
Artin groups were introduced at the beginning of the last century as a generalization of the well-known braid groups, the class of extra-large Artin groups was isolated in 1983, the class of Artin groups with a woody structure was isolated in 2003. The groups considered in this paper belong to almost large Artin groups and the problems of words and conjugacy of words are algorithmically solvable in them, which follows from the proof of their biautomaticity. The
approach proposed by the authors in solving the problem of power conjugacy of words is more
visual and simple.

The article describes the directions of research on the arithmetic properties of series values of the form

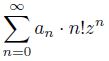
with coefficients 𝑎𝑛 satisfying certain conditions. Under these conditions, the considered series,
other than the polynomial, converges in the field C only at 𝑧 = 0. However, for almost all but a finite number of prime 𝑝 numbers, such a series converges in the fields Q𝑝. Therefore there are two ways of research. We can either consider the arithmetic properties of the result of some summation of this series, or consider the values of this series in the field Q𝑝. An example of the first approach is the series considered by Euler

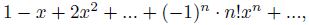
as a result of the summation of which, with the substitution 𝑥 = 1, we obtain the remarkable
equality

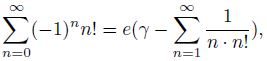
where 𝛾 – Euler’s constant.
Another direction of research uses the concept of global relation introduced by E. Bombieri.
Using the modified Siegel—Shidlovskii method, it is possible to obtain analogues of the main theorems of A.B. Shidlovskii for 𝐸− functions. The use of Hermite-Pade approximants made it possible to consider the values of generalized hypergeometric series not only with algebraic, but also with certain parameters transcendental in any field Q𝑝.

New cases of integrable dynamical systems of the fifth-order homogeneous in terms of variables are presented, in which a system on a tangent bundle to a two-dimensional manifold can be distinguished. In this case, the force field is divided into an internal (conservative) and an external one, which has a dissipation of different signs. The external field is introduced using some unimodular transformation and generalizes the previously considered fields. Complete sets of both the first integrals and invariant differential forms are given.

In the binomial random graph 𝐺(𝑛, 𝑝) edges between every pair of vertices appear independently with probability 𝑝. The random graph obeys 0-1 𝑘-law, if, for every first order sentence, the probability that 𝐺(𝑛, 𝑝) satisfies it is either 0 or 1 in the limit (as 𝑛 /∞). This paper addresses the following question: given a small 𝑘 and any ℓ, does 𝐺(𝑛, 𝑛−𝑙−1/ℓ) satisfy 0-1 𝑘-law? We answer this question for 𝑘 = 3 and all ℓ. We also prove that for 𝑘 = 4 and ℓ ∈ [1, 40] ∪ {72} 0-1 𝑘-law does not hold.

Incidence of a plane non-stationary sound wave on a homogeneous elastic cylinder in ideal liquid with a coating in the form of an elastic cylindrical layer with a density and elastic moduli continuously changing in thickness is considered. It is assumed that the front of the incident wave is parallel to the axis of rotation of the cylinder. The pressure field in the sound wave scattered by the body is found.
Mathematical model of the diffraction process under consideration is constructed, based on the linearized model of hydrodynamics of an ideal compressible fluid and a model of the linear theory of elasticity. The acoustic pressure in the fluid, equal to the sum of the pressures in the incident and scattered fields, is a solution to the wave equation. The propagation of elastic waves in a homogeneous cylinder is described by two wave equations with respect to the scalar and vector potentials of elastic displacements. In this case, due to the formulation of the problem,
the vector equation is reduced to a scalar equation. The wave process in an inhomogeneous elastic coating is described by the general equations of motion of a continuous medium and Hooke’s law. In addition to the above equations, the model includes: zero initial conditions, free slip conditions on the outer surface of the coating, rigid adhesion conditions on the inner surface of the coating, attenuation at infinity condition for the scattered acoustic field, and a boundedness condition for wave fields in the body.
Integral Laplace transform with respect to time and the method of separating variables by radial and angular coordinates are applied to the equations of the constructed model. In the image space, the sought pressure and potentials are represented as expansions in series in modified cylindrical Bessel functions taking into account the radiation and boundedness conditions. Images of the components of the displacement vector, normal and tangential stresses in the coating are sought in the form of Fourier series with unknown coefficients depending
on the radial coordinate. To determine them, a boundary value problem is constructed for a
system of linear ordinary differential equations of the first order. The boundary value problem is reduced to problems with initial conditions. The transition to the space of originals is carried out numerically. The results of pressure calculations in the acoustic field scattered by the body are presented.

The paper gives a short proof of the canonical Ramsey theorem of Erd˝os and Rado using ultrafilter theory.

In the article the problem of scattering of a plane monochromatic sound wave incident obliquely on a circular absolutely rigid cylinder covered by a radially inhomogeneous isotropic elastic layer is considered. The cylinder is located in a homogeneous ideal compressible fluid moving along forming of the cylinder with a constant subsonic speed.
The results of numerical calculations of directional patterns of a scattered acoustic field in the far zone for different laws of coating heterogeneity and values of the Mach number are presented.

The classical Liouville formula expressing the multiple integral over a multidimensional
pyramid through the integral over a segment is discussed. It is shown how the Liouville formula
is related to the special sum, containing successive antiderivatives of the integrand. Specific examples are given to illustrate the general result. Along the way, a compact formula for calculating the power moments of an exponential function is proved.

This article is devoted to the problem of studying meromorphic solutions of algebraic differential equations, which is traditional for the theory of differential equations. At the present, the case of the linear equations is quite well explored. Speaking of the nonlinear equations, there are relatively few results related to more or less common equation classes. There is one class of equations, where a number of results have been obtained. They are called Briot–Bouquet equations. These are the equations of the form 𝑃(𝑦, 𝑦(𝑛)) = 0, where 𝑃 is a complex polynomial, 𝑛 ∈ N. The research of the meromorphic solutions of this type of equations was started by Ch. Briot, J. C. Bouqet and Ch. Hermit, who described all possible solutions of the equations of the form 𝑃(𝑦, 𝑦′) = 0 by showing that they are all included in class 𝑊, which consists of rational
functions, rational functions of some exponential function and elliptic functions. After that E.
Picard’s work was published where he proved that all solutions of the equations of the form 𝑃(𝑦, 𝑦′′) = 0 are also included in 𝑊.
Later, the hypothesis arose that in any 𝑃(𝑦, 𝑦(𝑛)) = 0 equation (with some limitations to the 𝑃) all its meromorphic solutions are included in 𝑊. E. Hille, R. Kaufman, S. Bank, A. Eremenko, L. Liao, T. Ng, A. Yanchenko and other mathematicians have been working on its proof. Nowadays the validity of the hypothesis has been established in many cases, but there are a number of cases left, where it is neither proved nor disproved.
There is one of these cases described in this work. Exactly, equations 𝑦(𝑛) = 𝑦𝑚, where 𝑛,𝑚 ∈ N, 𝑚 ⩾ 2. A necessary and sufficient condition for the existence of nonzero meromorphic solutions of these equations and these solutions themselves are found.

The method for the formation of soft norms for complex systems operating under conditions
of uncertainty is presented, based on the methodology of Bayesian intelligent measurements
within the framework of the regularizing Bayesian approach. The implementation of the method is demonstrated using the example of agriculture in the Tula region.

The paper presents a lover estimate for the 𝑝-adic value of a polynomial evaluated at polyadic Liouville number.

The paper considers 𝐹-series 𝑓𝑖,𝑗(𝑧) = Σ︀∞
𝑛=0 (𝛼𝑖)𝑛(𝛽𝑗𝑧)𝑛, where 𝛼𝑖, 𝛽𝑗 are some rational
numbers. These series satisfy a system of first-order linear differential equations with coefficients from C(𝑧). Using previous results obtained using the approach proposed in one of the works of V.Kh. Salikhov, the algebraic independence of these series over C(𝑧) is established. Application of the general theorem on the arithmetic properties of 𝐹-series from the works of V.G. Chirsky, allows us to assert the infinite algebraic independence of the values of these series. This means that for any polynomial 𝑃 (𝑥1,1, . . . , 𝑥𝑚,𝑛) with integer coefficients other than the identical zero and any integer 𝜉 ̸= 0, there is an infinite set of prime numbers 𝑝 such that in the field Q𝑝 the inequality

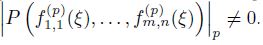Here the symbols 𝑓(𝑝) 𝑖𝑗 (𝜉) denote the sums of the
series Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛 (𝛽𝑗𝜉)𝑛 in the field Q𝑝.

The paper considers 𝐹-series 𝑓𝑖,𝑗(𝑧) = Σ︀∞
𝑛=0 (𝛼𝑖)𝑛(𝛽𝑗𝑧)𝑛, where 𝛼𝑖, 𝛽𝑗 are some rational
numbers. These series satisfy a system of first-order linear differential equations with coefficients from C(𝑧). Using previous results obtained using the approach proposed in one of the works of V.Kh. Salikhov, the algebraic independence of these series over C(𝑧) is established. Application of the general theorem on the arithmetic properties of 𝐹-series from the works of V.G. Chirsky, allows us to assert the infinite algebraic independence of the values of these series. This means that for any polynomial 𝑃 (𝑥1,1, . . . , 𝑥𝑚,𝑛) with integer coefficients other than the identical zero and any integer 𝜉 ̸= 0, there is an infinite set of prime numbers 𝑝 such that in the field Q𝑝 the inequality

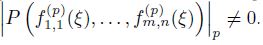Here the symbols 𝑓(𝑝) 𝑖𝑗 (𝜉) denote the sums of the
series Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛 (𝛽𝑗𝜉)𝑛 in the field Q𝑝.

This article investigates the following problem arising from the theory of products of sets. Let there be two finite subsets of the set of natural numbers, which throughout the article will be denoted as 𝐴 and 𝐵. We assume that they are a subset of the interval of numbers [1,𝑄]. By definition, we introduce a set called the product set 𝐴𝐵, the elements of which are represented as a product of elements from 𝐴,𝐵, in other words, such elements 𝑎𝑏, where 𝑎 ∈ 𝐴, 𝑏 ∈ 𝐵.
This article studies the problem of extremely large sets 𝐴 of a finite interval [1,𝑄] that have the asymptotically largest possible product, that is, the asymptotically largest value of |𝐴𝐴| equal to |𝐴|2/2. In the paper [2], a new non-trivial lower bound for the size of such a set 𝐴 was obtained in comparison with the previous result of the paper by K. Ford [1] and also of the paper [2]. In this article we present a method that improves the previous result, and also
introduce another version of this problem. In general, we follow and develop the formulations,
arguments, ideas and approaches proposed in the works [1], [2].