Пусть $ X-$ достаточно большое действительное число, $ b_{1},b_{2},b_{3} $- целые числа с условием $ 1\le {{b}_{1}},{{b}_{2}},{{b}_{3}}\le X,\,\,\, a_{ij}, (i=1,2,3;\,\,\, j=\overline{1.5})$ целые положительные числа, $p_{1},...,p_{5}-$ простые числа. Положим $ B=max\{3|a_{ij}|\} ,\,\,(i=1,2,3;\,\,j=\overline{1.5}), \vec{b} = (b_{1},b_{2},b_{3}),\,\, K=36\sqrt{3}B^{5}|\vec{b}|,\\ E_{3,5}(X)=card\{b_{i} |1\le {{b}_{i}}\le X,\,\,b_{i}\neq a_{i1}p_{1}+\cdots+a_{i5}p_{5},\,\,i=1,2,3\}$. В работе доказано, что система $b_{i}=a_{i1}p_{1}+\cdots+a_{i5}p_{5},\,\,(i=1,2,3)$ разрешимо в простых числах $p_{1},\cdots,p_{5}$, для всех троек $\vec{b}=(b_{1}, b_{2},b_{3}),\,\, 1\le {{b}_{1}},{{b}_{2}},{{b}_{3}}\le X$, за исключением не более чем $E_{3,5}(X)<X^{3-\varepsilon}$ троек из них, а также получена оценка снизу для $R(\vec{b})-$количество решений этой системы, то есть доказано справедливости неравенство $R(\vec{b})>> K^{2-\varepsilon}(\log K)^{-5}$, для всех $\vec{b}=(b_{1},b_{2},b_{3})$ за исключением не более чем $X^{3-\varepsilon}$ троек из них.

В этой статье мы вводим понятие сильно звездной I-компактности и изучаем некоторые ее топологические особенности. Мы представляем некоторые свойства конечных пересечений как для I-компактных пространств, так и для сильно звездных I-компактных пространств. Наконец, мы устанавливаем связь между счетно 𝐼𝑓𝑖𝑛-компактным пространством и сильно звездным 𝐼𝑓𝑖𝑛-компактным пространством. Для того чтобы выявить разницу между различными версиями компактности, мы приводим несколько контрпримеров.
Также в статье поставлены некоторые открытые проблемы.

Система находится в критическом состоянии, если даже небольшое возмущение может привести к глобальным изменениям. Таковы, например, любые фазовые переходы: в воде, охлаждённой до нуля градусов, один центр кристаллизации быстро разрастается до большого кластера. Впервые концепцию самоорганизующейся критичности предложили Бэк, Тэнг и Вайзенфелд в 1987 году. В своей работе они описали систему, ставшую классической моделью самоорганизующейся критичности: на квадратной сетке в некоторых узлах лежат песчинки, суммарно конечное число. Если в одном из узлов лежит более трёх песчинок, происходит обвал: четыре песчинки из этого узла перераспределяется на соседние узлы, это может вызвать обвалы в них, потом в их соседях... Обвалы будут лавинообразно происходить до тех пор, пока система вновь не вернется в равновесное состояние, этот процесс называется релаксацией.
В настоящей статье представлены результаты экспериментального и теоретического
исследования следующей задачи. Рассмотрим регулярный граф, вершинами которого являются точки плоскости, обе координаты которых целые, и каждая вершина соединена с 8 ближайшими вершинами. В точку (0,0) положим большое числе песчинок и произведём релаксацию. Результат релаксации имеет очевидную фрактальную структуру, видимую в компьютерных экспериментах, и части этой структуры могут быть описаны.
Мы классифицируем некоторые возникающие паттерны и предлагаем гипотезы о их устройстве (опираясь на похожие результаты для других регулярных графов). Доказаны оценки на среднее число песка в появляющихся паттернах.

В рамках нелинейного метода угловых пограничных функций существование решений нелинейных краевых задач доказывается через построение барьерных функций. Барьерные функции конструируются через выделенные специальным образом опорные барьеры. Сами опорные барьеры также могут выступать в роли барьерных функций. При этом приходится доказывать выполнение определенных неравенств, которые представляют самостоятельный функциональный интерес. Исследование этих неравенств приводит к
громоздким выкладкам. В настоящей работе предлагается способ, существенно упрощающий получение результатов. Возможные решения неравенств строятся в виде многочленов.
Начальный этап предполагает выделение многочлена наивысшей интересующей степени.
Такой многочлен называется коренным. Далее к коренному многочлену последовательно
добавляются многочлены низших степеней, называемые примыкающими многочленами.

В 1872 году Р. Дедекиндом была построено множество вещественных чисел R как некоторое расширение множества рациональных чисел Q способом взятия счётных порядковых регулярных сечений. Этот способ был обобщён и применён Г. Макнейлом к некоторым упорядоченным математическим системам. В данной статье способ Дедекинда – Макнейла применяется к математической системе 𝐶, порождённой семейством 𝐶𝑏(𝑇, 𝒢) всех непрерывных ограниченных функций 𝑓 : 𝑇 /R на тихоновском топологическом пространстве (𝑇, 𝒢).
Рассматривается дедекиндово расширение 𝐶 / / 𝐷(𝐶), а также счётно-дедекиндово расширение 𝐶 / / 𝐷0(𝐶), как более близкий аналог классического расширения Q / / R.
Даются функционально-факторные описания указанных расширений через семейства рав-
номерных функций относительно ансамблей подмножеств множества 𝑇, обладающих свой-
ством Стоуна и конуль-свойством Стоуна.
Даются характеризации указанных расширений как некоторых пополнений решёточного линейного пространства 𝐶, наделённого некоторой локальной структурой идеального
измельчения.
Функциональное описание и характеризация счётно-дедекиндова расширения 𝐶 / /𝐷0(𝐶) оказываются удивительным образом совпадающим с функциональным описанием и характеризацией риманова расширения 𝐶 / /𝑅𝜇, порождённого фактор-семейством всех функций на тихоновском пространстве (𝑇, 𝒢), 𝜇-интегрируемых по Риману относительно положительной ограниченной радоновской меры 𝜇.

Ивановым и Тужилиным была предложена одномерная проблема Громова о минимальном заполнении конечных метрических пространств, где в качестве заполнений рассматриваются взвешенные графы с неотрицательными весами ребер. Они показали, что задача редуцируется к случаю так называемых бинарных деревьев — деревьев у которых вершины имеют только степени 1 и 3. Ерёминым была получена минимаксная формула веса минимального заполнения. Формула Ерёмина использует понятие минимального параметрического заполнения — фиксируется граф (параметризация или тип); он показал, что вес минимального параметрического заполнения равен максимальному значению так называемого мультипириметра среди всех неприводимых мультиобходов.
Сложность структуры бинарного дерева можно измерять количеством так называемых усов — пар граничных вершин с общей смежной вершиной. Настоящая работа посвящена изучению мультиобходов бинарных деревьев с тремя усами. Найдена линейная рекуррентная формула для числа бинарных деревьев с тремя усами. Установлена связь между неприводимостью мультиобходов и включениями мультиграфов мультиобходов для
фиксированного бинарного дерева.
Недавно Щербаковым было доказано, что кратность неприводимого мультиобхода для
бинарного дерева с тремя усами не превосходит 2, в этой работе доказано существование
таких неприводимых мультиобходов у любого такого бинарного дерева.
Недавно Иванов и Тужилин предложили вычислять вес минимального параметрического заполнения, находя вершины многомерного многогранника допустимых значений переменных двойственной задачи линейного программирования с помощью компьютера.
Разработанная в настоящей работе техника позволяет найти все неприводимые мультиобходы у бинарного дерева с 6 граничными вершинами и 3 усами без использования компьютерных вычислений.

Строение алгебры Шевалле над полем или кольцом 𝐾, ассоциированной с неразложимой системой корней Φ, существенно зависит от ее нильтреугольной подалгебры 𝑁Φ(𝐾).
Для 𝑁Φ(𝐾) оказалось естественным использовать введенную в 2018 году точную обёртывающую алгебру 𝑅, имеющую один с 𝑁Φ(𝐾) базис. Известно, что изоморфность колец Ли 𝑁Φ(𝐾) не зависит от выбора знаков структурных констант 𝑁𝑟,𝑠. Однако, для точных обёртывающих колец 𝑅 это свойство нарушается. Поэтому вопрос описания их автоморфизмов был расширен до нахождения всех неизоморфных точных обёртывающих колец 𝑁Φ(𝐾) типа 𝐺2 над 𝐾, и только затем нахождения явного описания их автоморфизмов. Для класcических типов найдено описание автоморфизмов колец 𝑅 над любым
ассоциативно-коммутативным кольцом 𝐾 с единицей [13]. В статье перечислены все неизоморфные точные обёртывающие кольца 𝑁Φ(𝐾) типа 𝐺2 над произвольным ассоциативно-коммутативным кольцом 𝐾 с единицей. Также найдено явное описание их автоморфизмов.

В работе изучается асимптотика дискретного спектра оператора Штурма–Лиувилля, задаваемого на R+ выражением −𝑦′′+𝑞(𝑥)𝑦 и граничным условием в нуле 𝑦(0) cos 𝛼+𝑦′(0)
sin 𝛼 = 0, для быстро растущих на бесконечности потенциалов 𝑞(𝑥). Получены асимптотики собственных значений оператора для классов потенциалов, характеризующих скорость их роста на бесконечности.

Как известно, классическая задача (проблема) Аполлония о построении с помощью циркуля и линейки окружности, касающейся трёх данных, обладает конечным числом решений, либо не имеет решений, если заданные окружности концентрические. При этом допускаются так называемые вырожденные случаи: любая из данных окружностей может являться точкой, то есть окружностью нулевого радиуса, или прямой, то есть окружностью бесконечного радиуса.
Настоящая работа посвящена исследованию задачи Аполлония не для трёх окружностей, а для двух, включая вырожденные случаи. Представлена классификация всех случаев рассматриваемой задачи в зависимости от вида заданных объектов (точки, прямой или окружности) и от их взаимного расположения на вещественной координатной плоскости.
В каждом из приведённых случаев были не только найдены все решения, но и указаны
некоторые их взаимосвязи.
Подходы к решению полученных в классификации случаев основаны на понятии геометрического места точек, равноудалённых от заданных объектов задачи, и на условиях равенств расстояний от предполагаемого центра искомой касательной окружности до каждого из заданных объектов.
Отметим, что в отличие от классической задачи Аполлония решение всегда существует, более того, число решений бесконечно.

В теории приближений хорошо известны задачи о нахождении оценки наилучшего приближения через структурные свойства самой приближаемой функции. Работа посвящена
таким задачам в пространствах с несимметричной нормой и знакочувствительными весами.

В статье рассматриваются задачи, связанные с математической моделью экономического роста Рамсея – Касса – Купманса. Строится вспомогательная система дифференциальных уравнений, для которой удаётся получить решение в квадратурах. На основании полученного решения найдены оценки сверху функции потребления. Используя оценки
сверху для функции потребления, мы находим максимальное значение временного промежутка, на котором существуют решения вспомогательной системы дифференциальных
уравнений при рассматриваемых значениях параметров.
При специальном начальном условии нами показано, что существует решение задачи
Коши (𝐾(𝑡), 𝐶(𝑡)) на всем луче 𝑡 ∈ [0;+∞), причём, обе компоненты возрастают и стремятся к найденным нами значениям.

В данной работе предлагается алгоритм построения изоспектрального и частично-
изоспектрального операторов Дирака на конечном отрезке. Этот алгоритм применяется
к процессу нахождения решений смешанных задач, поставленных для систем дифференциальных уравнений с частными производными гиперболического типа с переменными коэффициентами.

Для одного класса полиномов Аппеля, ассоциированного с дифференциальным уравнением параболического типа, получены формулы коэффициентов разложения в ряд полиномов. Установлено, что полиномы Аппеля участвуют в формулах разложения решения
задачи Коши для уравнений параболического типа в ряд производных фундаментального решения. Предложен новый метод решения задачи Коши, суть которого состоит в применении разложения в ряды по полиномам Аппеля. Результаты обобщают метод решения уравнения теплопроводности на действительной оси разложением в ряд полиномов Эрмита. Исследована связь преобразования Фурье и рядов по ассоциированным полиномам Аппеля. Изучен вопрос применения полиномов Эрмита для преобразования Лапласа.

В статье строится такое поле 𝐸, что существует бесконечно много неизоморфных кватернионных 𝐸-алгебр с унитарными инволюциями и все такие алгебры расщепляются любым квадратичным расширением поля 𝐸.

Группы Артина являются обобщением известных групп кос, в последних алгоритмически разрешимы проблемы равенства и сопряженности слов. В силу сложности решения указанных проблем в классе групп Артина, алгоритмические проблемы рассматриваются в различных его подклассах.
В 1983 году К. Аппель и П. Шупп определили группы Артина экстрабольшого типа.
В 2003 году В. Н. Безверхний ввел в рассмотрение группы Артина с древесной структурой.
В статье рассматриваются обобщенные древесные структуры групп Артина, представляющие собой древесные произведения групп Артина экстрабольшого типа и групп Артина с древесной структурой, объединенных по циклическим подгруппам, соответствующим образующим этих групп.
Авторами статьи приводится оригинальное доказательство алгоритмической разрешимости проблемы обобщенной сопряженности слов в обобщенных древесных структурах групп Артина. Метод доказательства использует подход Г. С. Маканина, примененный им для исследования конечной порожденности нормализатора элемента в группах кос. Кроме того, в данной работе показывается, что централизатор конечно порожденной подгруппы в обобщенной древесной структуре групп Артина конечно порожден и существует алгоритм, выписывающий его образующие.

В статье рассматривается решение проблемы степенной сопряженности слов в обобщенных древесных структурах групп Артина геометрическими методами, основанными
на исследовании диаграмм над данным классом групп, имеющих однослойную структуру, как ранее показано авторами. Используются преобразования диаграмм, включающие
сокращения, введенные М. Деном и В. Н. Безверхним.
Статья является продолжением рассмотрения алгоритмов для решения проблем комбинаторной теории групп в обобщенных древесных структурах групп Артина, ранее авторами предлагались алгоритмы, основанные на диаграммном подходе, для решения проблем
сопряженности, обобщенной сопряженности слов, построения централизаторов элемента и
конечно порожденной подгруппы.
Рассматриваемый в статье класс групп представляет собой древесное произведение
групп Артина с древесной структурой и групп Артина экстрабольшого типа, объединение
ведется по бесконечным циклическим подгруппам, порожденным образующими соответствующих групп.
Группы Артина введены в начале прошлого века как обобщение известных групп кос, класс групп Артина экстрабольшого типа выделен в 1983 году, класс групп Артина с древесной структурой определен в 2003 году. Рассматриваемые в работе группы относятся к почти большим группам Артина и в них алгоритмически разрешимы проблемы равенства, сопряженности слов, что следует из доказательства их биавтоматности. Предложенный авторами подход в решении проблемы степенной сопряженности слов является более наглядным и простым.

Статья посвящена описанию направлений исследования арифметических свойств значений рядов вида

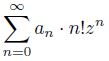с коэффициентами 𝑎𝑛, удовлетворяющими определённым условиям. При этих условиях
рассматриваемый ряд,отличный от многочлена, сходится в поле C только при 𝑧 = 0. Однако для почти всех, кроме конечного числа, простых чисел 𝑝 такой ряд сходится в полях Q𝑝.Поэтому есть два естественных пути исследования. Мы можем рассматривать либо значения результата некоторого суммирования этого ряда, либо его значения в поле Q𝑝. Примером первого подхода служит рассмотренный ещё Эйлером ряд

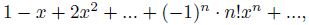в результате суммирования которого при подстановке 𝑥 = 1 получается замечательное
равенство

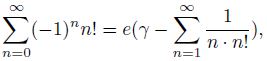где 𝛾− постоянная Эйлера.
Другое направление исследований использует введённое Э.Бомбиери понятие глобального соотношения. Используя модифицированный метод Зигеля–Шидловского удаётся получить аналоги основных теорем А.Б.Шидловского для 𝐸− функций. Применение аппроксимаций Эрмита-Паде позволило рассмотреть значения обобщённых гипергеометрических рядов не только с алгебраическими, но и с некоторыми трансцендентными в любом поле Q𝑝 параметрами.

Представлены новые случаи интегрируемых однородных по части переменных динамических систем пятого порядка, в которых может быть выделена система на касательном расслоении к двумерному многообразию. При этом силовое поле разделяется на внутреннее (консервативное) и внешнее, которое обладает диссипацией разного знака. Внешнее поле вводится с помощью некоторого унимодулярного преобразования и обобщает ранее рассмотренные поля. Приведены полные наборы как первых интегралов, так и инвариантных дифференциальных форм.

В биномиальном случайном графе 𝐺(𝑛, 𝑝) ребра проводятся независимо и с вероятностью 𝑝 каждое. Случайный граф подчиняется 𝑘-закону 0 или 1, если вероятность истинности любой формулы первого порядка, кванторная глубина которой не превосходит 𝑘, стремится либо к 0 либо к 1 при 𝑛 /∞. Данная статья посвящена ответу на следующий вопрос: для каких пар 𝑘 и ℓ случайный граф 𝐺(𝑛, 𝑛−𝑙−1/ℓ) подчиняется 𝑘-закону 0 или 1? Мы получили полный ответ при 𝑘 = 3 и всех натуральных ℓ, а также доказали, что при 𝑘 = 4 и ℓ ∈ [1, 40] ∪ {72} закон нарушается.

Рассматривается падение плоской нестационарной звуковой волны на находящийся в идеальной жидкости однородный упругий цилиндр с покрытием в виде упругого цилиндрического слоя с непрерывно изменяющимися по толщине плотностью и модулями упругости. Полагается, что фронт падающей волны параллелен оси вращения цилиндра. Отыскивается поле давления в рассеянной телом звуковой волне.
Построена математическая модель рассматриваемого дифракционного процесса, основанная на линеаризованной модели гидродинамики идеальной сжимаемой жидкости и модели линейной теории упругости. Акустическое давление в жидкости, равное сумме давлений в падающем и рассеянном полях, является решением волнового уравнения. Распространение упругих волн в однородном цилиндре описывается двумя волновыми уравнениями относительно скалярного и векторного потенциалов упругих смещений. При этом в силу постановки задачи векторное уравнение приводится к скалярному уравнению. Волновой процесс в неоднородном упругом покрытии описывается общими уравнениями движения сплошной среды и законом Гука. Помимо указанных выше уравнений модель включает: нулевые начальные условия, условия свободного проскальзывания на внешней поверхности покрытия, условия жесткого сцепления на внутренней поверхности покрытия, условие затухания на бесконечности для рассеянного акустического поля и условие ограниченности для волновых полей в теле.
К уравнениям построенной модели применяется интегральное преобразование Лапласа по времени и метод разделения переменных по радиальной и угловой координатам. В
пространстве изображений искомые давление и потенциалы представляются в виде разложений в ряды по модифицированным цилиндрическим функциям Бесселя с учетом условий излучения и ограниченности. Изображения компонент вектора смещения, нормального и касательного напряжений в покрытии ищутся в виде рядов Фурье с неизвестными, зависящими от радиальной координаты коэффициентами. Для их определения построена краевая задача для системы линейных обыкновенных дифференциальных уравнений первого порядка. Краевая задача сведена к задачам с начальными условиями. Переход в пространство оригиналов осуществлен численно. Представлены результаты расчетов давления в рассеянном телом акустическом поле.

В статье дается короткое доказательство канонической рамсеевской теоремы Эрдёша
и Радо с использованием теории ультрафильтров.

В статье рассматривается задача о рассеянии плоской монохроматической звуковой волны, падающей наклонно на круговой абсолютно жесткий цилиндр, покрытый радиально-неоднородным изотропным упругим слоем. Цилиндр находится в однородной идеальной сжимаемой жидкости, движущейся вдоль образующей цилиндра с постоянной
дозвуковой скоростью.
Получено аналитическое решение задачи.
Представлены результаты численных расчетов диаграмм направленности рассеянного акустического поля в дальней зоне при разных законах неоднородности покрытия и значениях числа Маха.

Обсуждается классическая формула Лиувилля, выражающая кратный интеграл по многомерной пирамиде через интеграл по отрезку. Показано, как формула Лиувилля связана со специальной суммой, содержащей последовательные первообразные подынтегральной функции. Приведены конкретные примеры, иллюстрирующие общий результат. Попутно доказана компактная формула для вычисления степенных моментов экспоненциальной функции.

Данная статья посвящена задаче изучения мероморфных решений алгебраических
дифференциальных уравнений, являющейся традиционной для теории дифференциальных уравнений. К настоящему времени достаточно хорошо исследован случай линейных уравнений. Что касается нелинейных уравнений, то здесь результатов, относящихся к более или менее общим классам уравнений, сравнительно немного. Одним из классов алгебраических дифференциальных уравнений, где получен ряд общих результатов, являются так называемые уравнения типа Брио-Буке. Это уравнения вида 𝑃(𝑦, 𝑦(𝑛)) = 0, где 𝑃 — многочлен с комплексными коэффициентами, 𝑛 ∈ N. Исследование мероморфных решений уравнений такого типа начато в работах Ш. Брио, Ж. К. Буке и Ш. Эрмита, которые описали все возможные решения уравнений вида 𝑃(𝑦, 𝑦′) = 0, показав, что все они лежат в классе 𝑊, состоящем из рациональных функций, рациональных функций от некоторой
экспоненциальной функции и эллиптических функций. Далее была опубликована работа
Э. Пикара, который доказал, что все решения уравнений вида 𝑃(𝑦, 𝑦′′) = 0 также лежат в
𝑊.
В дальнейшем возникла гипотеза о том, что у любого уравнения вида 𝑃(𝑦, 𝑦(𝑛)) = 0 (при некоторых ограничениях на многочлен 𝑃) все мероморфные решения лежат в 𝑊. Над
доказательством этой гипотезы работали Э. Хилле, Р. Кауфман, С. Бэнк, А. Ерёменко, Л.
Лиао, Т. Нг, А. Янченко и другие математики. К настоящему времени справедливость гипотезы установлена во многих случаях. Остается, однако, ряд случаев, в которых гипотеза не доказана и не опровергнута.
В данной работе рассмотрен один такой случай, а именно уравнения 𝑦(𝑛) = 𝑦𝑚, где 𝑛,𝑚 ∈ N, 𝑚 ⩾ 2. Найдено необходимое и достаточное условие существования ненулевых мероморфных решений указанных уравнений и сами эти решения.

Представлен метод формирования мягких норм для сложных систем, функционирующих в условиях неопределенности, на основе методологии байесовских интеллектуальных
измерений в рамках регуляризирующего байесовского подхода. Продемонстрирована реа-
лизация метода на примере сельского хозяйства Тульской области.

В статье установлены оценки многочлена от полиадического Лиувиллева числа в 𝑝- адической области.

В работе рассматриваются 𝐹–ряды 𝑓𝑖,𝑗(𝑧) =
Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛(𝛽𝑗𝑧)𝑛, где 𝛼𝑖, 𝛽𝑗 – некоторые рациональные числа. Эти ряды удовлетворяют системе линейных дифференциальных уравнений первого порядка с коэффициентами из C(𝑧). Используя предыдущие результаты, полученные с помощью подхода, предложенного в одной из работ В.Х. Салихова, устанавливается алгебраическая независимость этих рядов над C(𝑧). Применение общей теоремы об арифметических свойствах 𝐹–рядов из работ В.Г. Чирского, позволяет утверждать бесконечную алгебраическую независимость значений этих рядов. Это означает, что для любого многочлена 𝑃 (𝑥1,1, . . . , 𝑥𝑚,𝑛) с целыми коэффициентами, отличного от тождественного нуля и любого целого числа 𝜉 ̸= 0, существует бесконечное множество простых чисел 𝑝 таких что в поле Q𝑝 выполняется неравенство

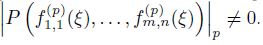
Здесь символы 𝑓(𝑝) 𝑖𝑗 (𝜉) обозначают суммы рядов Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛 (𝛽𝑗𝜉)𝑛 в поле Q𝑝.

В работе рассматриваются 𝐹–ряды 𝑓𝑖,𝑗(𝑧) =
Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛(𝛽𝑗𝑧)𝑛, где 𝛼𝑖, 𝛽𝑗 – некоторые рациональные числа. Эти ряды удовлетворяют системе линейных дифференциальных уравнений первого порядка с коэффициентами из C(𝑧). Используя предыдущие результаты, полученные с помощью подхода, предложенного в одной из работ В.Х. Салихова, устанавливается алгебраическая независимость этих рядов над C(𝑧). Применение общей теоремы об арифметических свойствах 𝐹–рядов из работ В.Г. Чирского, позволяет утверждать бесконечную алгебраическую независимость значений этих рядов. Это означает, что для любого многочлена 𝑃 (𝑥1,1, . . . , 𝑥𝑚,𝑛) с целыми коэффициентами, отличного от тождественного нуля и любого целого числа 𝜉 ̸= 0, существует бесконечное множество простых чисел 𝑝 таких что в поле Q𝑝 выполняется неравенство

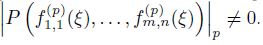
Здесь символы 𝑓(𝑝) 𝑖𝑗 (𝜉) обозначают суммы рядов Σ︀∞ 𝑛=0 (𝛼𝑖)𝑛 (𝛽𝑗𝜉)𝑛 в поле Q𝑝.

В статье исследуется следующая задача, возникающая из теории произведений множеств. Пусть имеются два конечных подмножества из множества натуральных чисел, которые всюду в статье будут обозначаться как 𝐴 и 𝐵. Полагаем, что они являются подмножеством интервала чисел [1,𝑄]. Вводим по определению множество, которое называется множеством произведения 𝐴𝐵, элементы которого представляются в виде произведения элементов из 𝐴,𝐵, иными словами такие 𝑎𝑏, где 𝑎 ∈ 𝐴, 𝑏 ∈ 𝐵. В данной статье изучается задача об экстремально больших множествах 𝐴 конечного интервала [1,𝑄], которые обладают асимтотически наибольшим возможным произведением, то есть асимптотически наибольшим значением |𝐴𝐴| равным |𝐴|2/2. В работе [2], была получена новая нетривиальная нижняя оценка на размер такого множества 𝐴 по сравнению с предыдущим результатом статьи К.Форда [1]. В данной статье мы представляем метод , который улучшает
предыдущий результат, а также рассматриваем другую версию этой задачи. В целом мы
следуем и развиваем формулировки, аргументы, идеи и подходы предложенные в работах
[1], [2].