Non homogeneous Beatty sequences play important rules in Wythoff games and invariant games such as on how to beat your Wytoff games opponent on three fronts and give properties into a decision of the procedure relying only on a few algebraic tests. This paper discusses on the cardinality of character sums and their estimation with respect to non homogeneous Beatty sequences 𝛽𝛼 = ⌊𝛼𝑛 + 𝛽 : 𝑛 = 1, 2, 3...⌋ where 𝛽 in real numbers and 𝛼 greater than zero is
irrational. In order to estimate the cardinality, the discrepancy is used to measure the number of uniform distribution for Beatty sequences. Pigeonhole principle is discussed on the estimation of the fractional part of Beatty sequences involve. Meanwhile, Cauchy inequalities is applied to expand the double character sums. Then, the cardinality of double character sums is obtained by applying the extension properties of additive and multiplicative character sums. The result
obtained is depend on the existing of identity of additive and multiplicative character sums and the uniformly distribution modulo 1. The result of the estimation in this study over composite modules is more general compared to previous studies, which only cover prime modules.

The coverings are mostly used in geometry and analysis, and sometimes they are not given explicitly. The problem on defining of covering in concrete situation is substantive. Coverings arose in theory of manifolds, especially in connection with the system of equations. One of powerful methods in this direction is a theorem on implicit functions.
In the paper we study these questions in a necessary general form. Such a consideration lead the problems to the basic notions which were studied by classics of mathematics in last two centuries. By him it was analyzed the main points of the theory on behavior of manifolds of less dimensions in manifolds of higher dimensions. Defining of the notion of a curve in the plane is bright example showing how we can establish suitable properties of objects we deal with to get
the necessary freedom of actions, does not avoiding simplest generality. Introducing of quadrable curves makes possible to develop an acceptable notion of the integral in the domains on the plane. But this is insufficient for establishing for example, the theorem of Fubini on repeated integrals in that form as in Lebesgue’s theory. Here we rest to constraints brought by intersection of manifold with boundary. The useful formulation of this theorem is possible to get only in
Lebesgue theory of integration. This is one of multiplicity of questions connected with behavior of manifolds of less dimensions. We show how some notions of the theory must be modified to avoid such difficulties. We establish that the generalization of a notion of "improper"surface integral in some different from the ordinary meaning, makes possible solve the problem in general.
In the present work we lead by such method the question on estimating of the number of sheets of covering to some metric relations connected with surface integrals.

In the proposed work, we construct a regularized asymptotics for the solution of a singularly perturbed inhomogeneous Cauchy problem for the Schrodinger equation. The potential 𝑞(𝑥) = 𝑥^2 chosen in the paper leads to a singularity in the spectrum of the limit operator in the form of a strong turning point. The main problem that the researcher faces when applying the regularization method is related to the search and description of regularizing functions that contain a non-uniform singular dependence of the solution of the desired problem,
highlighting which, you can search for the rest of the solution in the form of power series in a small parameter. The development of the regularization method led to the understanding that this search is closely related to the spectral characteristics of the limit operator. In
particular, it is established how the singular dependence of the asymptotic solution on a small parameter should be described under the condition that the spectrum is stable. When stability conditions are violated, things are much more complicated. Moreover, there is still no complete mathematical theory for singularly perturbed problems with an unstable spectrum, although they began to be studied from a general mathematical standpoint about 50 years ago. Of particular interest among such problems are those in which the spectral features are expressed in the form of point instability. In papers devoted to singularly perturbed problems, some of the singularities of this type are called turning points. Based on the ideas of asymptotic integration
of problems with an unstable spectrum by S.A. Lomov and A.G. Eliseev, it is indicated how and from what considerations regularizing functions and additional regularizing operators should be introduced, the formalism of the regularization method for the problem posed is described in detail, and justification of this algorithm and an asymptotic solution of any order with respect to a small parameter is constructed.

In this paper a new proof of the L’Hˆopital’s rule proposed for calculus lecturers is presented. The according theorem is formulated and proved for the six types of limit: 𝑥 → 𝑎, 𝑥 → 𝑎 + 0, 𝑥 → 𝑎 − 0, 𝑥 → +∞, 𝑥 → −∞, 𝑥 → +∞, for the two indeterminate forms 0/0 and ∞/∞ and also for four values of limit 𝐴 ∈ (−∞,+∞), 𝐴 = −∞, 𝐴 = +∞, 𝐴 = ∞. Thus, the theorem covers 6 * 2 * 4 = 48 cases of the L’Hˆopital’s rule. The presented proof of the theorem differs from the traditional ones by using not only the Cachy definition of limit a function but also the Heine one. The single partial limit theorem is used as the important auxiliary statement allowing to apply the Heine definition of limit. This statement also allows to apply arithmetic properties of sequence limits to the proof of the indeterminate form ∞/∞ and the limit 𝑥 → 𝑎 + 0, i.e. for the case where the most significant simplification is achieved.

For modeling a fractured rock mass, it is necessary to have information about the geometric characteristics of the fractures - their sizes, orientations, and numbers.
As a result of geological surveys and observations during mining operations, data are obtained on the number and orientation of fracture traces.
This leads to the tasks of restoring the spatial pattern of the fracture distribution on surfaces or through boreholes. The tasks that actually arise here are tomography tasks. This work is dedicated to their mathematical formulation and reduction to classical problems of finding the inverse Radon transform.
In this work, when considering the tasks of finding the distribution of fractures by orientation alone, under a fracture we will understand a section of a flat surface, having an arbitrary shape.
In solving the problem of finding the joint distribution of fractures by size and orientation, we will consider the fractures to be disc-shaped. Assuming, for example, elliptical fractures makes the problem unsolvable. This is because an elliptical fracture is defined by five parameters: the orientation of the plane, the direction of the main axes, and their magnitudes. Therefore, the distribution function of such fractures by shapes and orientations is a function of five variables.
On the other hand, the distribution function of fracture traces by sizes and orientations is already a function of four variables - the direction of the intersecting plane and the size and direction of the trace there. Therefore, the task of finding the distribution of fractures for elliptical fractures, generally speaking, is not solvable unambiguously, which is why disc-shaped fractures are assumed.

The article investigates the classification with precision up to equivalence of involutions in the algebra of upper triangular matrices over the ring of integers of algebraic numbers of quadratic fields.
The description of involutions in algebras represents one of the classical problems of ring theory. Standard examples of involutions are transposition in matrix algebra and conjugation in the field of complex numbers and the algebra of quaternions.
In the case where the field 𝑃 has a characteristic different from two, a complete description of involutions with precision up to their equivalence in the algebra 𝑇𝑛(𝑃) for any natural number 𝑛 was obtained in [15]. In this work [3] involutions in the algebra of upper triangular matrices over commutative rings are studied. If the ring is a field of characteristic 2 or a Boolean ring, then necessary and sufficient conditions for the finiteness of the number of equivalence classes
of involutions were found.
This article is a continuation of the work of [3]. In the article [3], in particular, the number of equivalence classes of involutions in the algebras of upper triangular matrices over the ring of integers was found. In this regard, the natural result is the problem of describing involutions with precision up to their equivalence in algebras of upper triangular matrices over the ring of algebraic integers of quadratic fields, to which this work is devoted. In the work, the  number of equivalence classes of involutions in such algebras is found and the method of finding representatives in each equivalence class is illustrated with examples. Upon receipt the main results in this work, the apparatus of the theory of Pell’s equations is significantly used.

We consider a regression statement of the problem of estimating the mean function of some almost sure continuous random process, when noisy values of independent copies of this random process are observed in some known sets of time points (generally speaking, random). Moreover, the size of observations for each of the copies is random, and the total collection of the time points for all series does not necessarily consist of independent and identically distributed random variables. This setting includes two of the most popular sparse data variants in the scientific literature, in which ever the sizes of observations in the series are independent identically distributed random variables, or the sizes of observations in each series are nonrandom and uniformly bounded over all series.
The paper proposes new kernel-type estimators for the mean function of a random process.
The uniform consistency of the new kernel estimators is proved under very weak and universal restrictions regarding the stochastic nature of observed time points: it is only required that the entire set of these points with a high probability would form a refining partition of the original random process domain.

In the case of Lie algebras g of small dimension ≤ 7, an enhanced version of the Generalised argument shift conjecture is proved, namely, it is shown that for any element 𝑎 ∈ g* on the dual space g* there is a complete set of polynomials in the bi-involution with respect to the standard Poisson-Lie bracket and the frozen argument bracket associated with the covector 𝑎.

The work contains results in which representations of subharmonic functions on the most mentioned sets in a half-plane — in a half-ring and in a half-disk — are given. Classical results in this direction are, for example, the Nevanlinna, Poisson-Jensen and Shimizu-Ahlfors formulas of the representation of a meromorphic function in a closed disk and in a closed half-disk, as well as the Riesz-Martin theorem on the representation of subharmonic functions. In the works of T. Carleman (1933) and B. Ya. Levin (1941) for functions that are analytic and meromorphic in the closure of a half-ring and in the closure of a half-disk on the complex plane, formulas that relate the logarithm of the modulus of a function with the location of its zeros and poles were obtained. These formulas have found numerous applications in the theory of entire and meromorphic functions. Independently of each other, Jun-Iti Ito and A. F. Grishin (1968) extended the Levin and Carleman formulas to subharmonic functions in an open half-disk. Note, however, that Grishin’s formulas using the Martin function, in our opinion, are more visual and convenient for practical use. In addition, A. F. Grishin formulated (without proof) a theorem
on the representation of a subharmonic function in a semi-open half-ring. N. V. Govorov (1968) extended the Levin and Carleman formulas to analytic functions in a semi-closed half-disk and in a semi-closed half-ring. By the expression "semi-closed set"we mean a set on the complex plane, part of the boundary of which belongs to the set, and the rest of the boundary does not belong to it. In particular, by a semi-closed half-ring or a semi-closed half-disk in the upper half-plane of a complex variable we mean a half-ring or half-disk whose intersection of boundary with the real axis does not belong to the given set.
In the article, we extend Grishin’s formula to subharmonic functions in an open half-ring.
We introduce the concept of full measure of a subharmonic function in an open half-ring, which generalizes the concept of full measure in the sense of Grishin. Due to this, the representation of the subharmonic function in the open half-ring, which is the simplest in form and with the least restrictions on the function, is obtained.

The nearly trans-Sasakian manifolds, which are almost 𝐶(𝜆)-manifolds, are considered. On the space of the adjoint G-structure, the components of the Riemannian curvature tensor, the Ricci tensor of the nearly trans-Sasakian manifolds, and the almost 𝐶(𝜆)-manifolds are obtained.
Identities are obtained that are satisfied by the Ricci tensor of nearly trans-Sasakian manifolds.
It is proved that a Ricci-flat almost 𝐶(𝜆)-manifold is locally equivalent to the product of a Ricciflat K¨ahler manifold and a real line. Identities are obtained that are satisfied by the Ricci tensor of an almost 𝐶(𝜆)-manifold. It is proved that the Ricci curvature of an almost 𝐶(𝜆)-manifold in the direction of the structure vector is equal to zero if and only if it is cosymplectic, and hence locally equivalent to the product of a K¨ahler manifold and a real line. An identity is obtained that is satisfied by the Riemannian curvature tensor of a nearly trans-Sasakian manifold, which is an almost 𝐶(𝜆)-manifold. It is proved that for a nearly trans-Sasakian manifold M the following conditions are equivalent: 1) the manifold M is an almost 𝐶(𝜆)-manifold; 2) the manifold M is a closely cosymplectic manifold; 3) the manifold M is locally equivalent to the product of a nearly K¨ahler manifold and the real line. In the case when the manifold M is a trans-Sasakian almost
𝐶(𝜆)-manifold, the manifold M is cosymplectic, and hence locally equivalent to the product of a K¨ahler manifold and a real line. For an NTS-manifold of dimension greater than three, which is almost a 𝐶(𝜆)-manifold, the pointwise constancy of the Φ-holomorphic sectional curvature implies global constancy. A complete classification of such manifolds is obtained.

In this paper we describe a reasoning method which allows to get relatively simple estimates of cotangent values for angles in the half-interval (0, 𝜋/2 ]. The method is based on the ability of the cotangent to refine some of its estimates that were derived from other considerations. As an illustration of the method we give cotangent estimates for two subclasses of rational functions.

The focus of the article is the classical Faa Di Bruno formula for computing higher-order derivatives of a complex function 𝐹(𝑢(𝑥)). Here is a version of the proof of this formula. Then we prove a generalization of the Faa Di Bruno formula to the case of a complex function with an inner function 𝑢(𝑥, 𝑦) depending on two independent variables. The paper presents a formula for the 𝑛-th derivative of a complex function, when the argument of the outer function is a
vector with an arbitrary number of components (functions of one variable). The article also considers examples of finding higher-order derivatives, illustrating both the classical Faa Di Bruno formula and its generalizations.

The problem of enumerating a class of polyhedra with given symmetry conditions is one of the important problems of the modern theory of convex polyhedra. There are many works in which the problem of a complete enumeration of polyhedra with symmetry conditions is posed.
If we limit ourselves to polyhedra in 𝐸3, then examples of such polyhedra are regular, regular stellate, Archimedean polyhedra, the Johnson-Zalgaller class, polyhedra with conditional edges, and polyhedra with parquet faces. Specifically, the symmetry conditions for the class of closed convex regular polyhedra consist in the conditions that the polyhedron’s equal faces are regular and its vertices are of the same type. For Johnson-Zalgaller polyhedra — under the condition
that the faces of a closed convex polyhedrons are regular. It is known that the last class, in addition to regular and Archimedean polyhedra, is an infinite series prisms and antiprisms, contains 92 polyhedra with regular faces.
Previously, the author found new classes of polyhedra (for example, the so-called polyhedra that are strongly symmetric with respect to rotation); they have such a symmetry of elements in which the conditions for the regularity of the faces are not presupposed. At the same time, the completeness of the lists of the considered classes was proven.
Returning to such symmetry conditions, which include the conditions of regularity of faces, the author introduced a class of closed convex 𝑅𝑅-polytopes (from the words rhombic and regular). Briefly, this class is defined by the following symmetry conditions. The faces of an
𝑅𝑅-polytope can be divided into two non-empty disjoint sets — a set of equal symmetrical rhombic stars that do not have common edges, and a set of regular faces.
Moreover, a vertex 𝑉 is called rhombic if the faceted star 𝑆𝑡𝑎𝑟(𝑉 ) of a vertex 𝑉 of the polyhedron consists of 𝑛 equal and identically spaced rhombuses (not squares) having a common vertex 𝑉 . If the vertex 𝑉 belongs to the rotation axis of order 𝑛 of the star 𝑆𝑡𝑎𝑟(𝑉 ), then 𝑉 is
called symmetric. A symmetric rhombic vertex 𝑉 is called obtuse if the rhombuses of the star 𝑆𝑡𝑎𝑟(𝑉 ) at the vertex 𝑉 meet at their obtuse angles. An example of a 𝑅𝑅-polyhedron is the elongated rhombic dodecahedron.
This paper provides a modified proof of the theorem on the existence and uniqueness of a closed convex 𝑅𝑅-polyhedron associated with the icosahedron and proves the existence of a twenty-fourth 𝑅𝑅-polyhedron with triangular faces and four obtuse rhombic vertices. Theorems on the non-existence of certain polyhedra with regular faces of various types, “close” to 𝑅𝑅-polytopes, have also been proven.

The paper considers the direct problem of diffraction of a harmonic sound wave by a set of linearly elastic bodies. The statement of the problem of the diffraction of a plane acoustic wave propagating in an ideal fluid by a given set of inhomogeneous anisotropic elastic bodies
is presented. The problem statement is two-dimensional. As a method for solving the problem, a modification of the finite element method is proposed. Both the general idea of the method as applied to diffraction problems and the algorithm for solving this problem are described.
For discretization in the space surrounding elastic bodies, in the two-dimensional case, a region bounded by a circle is selected. The area is divided into elements: in this work, it is proposed to use triangular elements of the first order. For each triangular element, a local matrix is built, the structure of which is based on the Helmholtz equation (for liquid elements) or general equations of motion of a continuous medium and Hooke’s law (for elastic elements), as well as boundary
conditions. Local matrices of elements make it possible to form a sparse global matrix for a system of linear algebraic equations, the solution of which determines the required values of pressure and displacements at the grid nodes. The interpolation procedure makes it possible to calculate the pressure and displacements at an arbitrary point inside the region, and the boundary conditions determine the scattered wave at points outside the region.

For an elastic symmetric body in the form of a layer weakened by a hole and loaded in mode 1, the concept of an interaction arc (IA) is introduced. The IA forms a small neighborhood of the point of maximum specific free energy in the middle section of the layer. The free energy flow through IA is represented by the energy product (EP) - the product of the specific free energy and a linear parameter. Using the well-known asymptotic expressions for the stress field in the neighborhood of the hole apex, a relationship is obtained between the linear parameter and the radius of curvature of the hole apex, which ensures the independence of the EP from the radius of curvature and the linear parameter. When the radius of curvature is zero, the
hole degenerates into a mathematical cut. In this case, the EP is reduced to the Irwin formula.
Thus, if any hole degenerates into a mathematical cut, then regardless of the geometry of the cut edges, in the limit, we must come to the same stress intensity factor (SIF). In particular, we use a semi-elliptical hole. A technique for determining the SIF-1 is proposed, based on the
representation of the approximating SIF in terms of dimensionless free energy flows that take a stationary value as the radius of curvature tends to zero. The values of the SIF obtained by this method coincide with their values given in other sources based on the analysis of the disclosure of the mathematical cut. In particular, a rectangular layer subjected to a distributed load is considered. The solutions were obtained by the FEM using the CAE Fidesys software package.
The difference with the known results was less than one percent.

The energy of interchange, like many other characteristics, is a periodic property of the position of the element in the D.I. Mendeleev. To establish this periodicity, a graph is used that represents the dependence of the energy of interchange of indium with other elements on their serial number.
Graphically depicting the dependence of the energy of interchange within individual groups (IC) on the charge of the nucleus between atoms, it is possible to establish new patterns. Based on the concept of varieties of types of state diagrams, showing the mutual solubility of elements in each other both in liquid and solid states, depending on temperature and pressure, these regularities can be given a satisfactory explanation.

The article considers the diffraction of sound waves by an inhomogeneous isotropic cylindrical shell of finite length of arbitrary thickness. It is assumed that there is a vacuum in the cavity of the cylindrical shell. The density and elastic modulus of the shell material are described by continuous functions of the radial coordinate. The primary field of disturbances is a plane harmonic sound wave falling obliquely on the body.
For the scattered field, a representation in the form of the Helmholtz-Kirchhoff integral is used. It is shown that the use of quadrature formulas for parallelepipedal Korobov grids makes it possible to reduce the number of calculations with approximate calculation of integrals. This method is compared with the calculation of integrals by the method of sequential integration using the quadrature formula of trapezoids. The calculation time of the field potential scattered
by a finite cylindrical shell is compared by two methods of calculating integrals.
A significant effect of the inhomogeneity of the shell material on the sound-reflecting properties of elastic cylindrical bodies has been revealed.

In paper the problem of the diffraction of a spherical monochromatic sound wave on a homogeneous isotropic elastic cylinder with a radially inhomogeneous elastic coating located near the boundary of half-spaces. It is assumed that the cylinder is located in the upper halfspace filled with an ideal homogeneous liquid bordering on a homogeneous elastic half-space.
To represent a scattered field in an ideal fluid, a representation in the form of the Helmholtz-Kirchhoff integral is used, which is subsequently reduced to a system of linear algebraic equations with respect to the Fourier coefficients of the corresponding expansions of the total potential of the field and its normal derivative in a liquid half-space.
The oscillations of an inhomogeneous isotropic elastic layer are described by the general equations of motion of a continuous medium. To find the displacement field in an inhomogeneous
coating, a boundary value problem for a system of second-order ordinary differential equations is constructed.
The asymptotic formula for the far field zone is obtained by the steepest descent method.
Numerical calculations of the angular characteristics of the scattered field are presented. A significant influence of continuously inhomogeneous coatings, as well as the presence of a plane near a cylindrical diffuser, on the diffraction pattern of the scattered field is revealed.

Authors of paper put before themselves a problem: to acquaint the mathematical public with unpublished paper of the outstanding Soviet mathematician M.I.Kadets heading the Kharkov school, known for the works in the field of the theory of Banach spaces, to tell story of this
paper. The given work continues paper of the author about part cooperation and interaction of teachers and scientists of the Tula state pedagogical university of L.N.Tolstoy and Michael Iosifovich Kadetsa’s Kharkov school.
Under its management the Tula student which afterwards after training at Michael Iosifovich Kadetsa’s Kharkov school became the candidate of physical and mathematical sciences conducted scientific work. Michael Iosifovich by right is considered one of founders of the
theory of equivalent renormings of the Banach spaces, turned now in independent area. The Kharkov school Kadetsa has at that time become world-famous. M.I.Kadets generously shared the mathematical ideas with the pupils. In paper some joint outcomes received by M.I.Kadetsem and its pupil in 1988-1990 which prepared for the publication in the form of joint paper but then have not been published because of high insistence which was shown to itself by outstanding Soviet mathematician M. I. Kadets, to insistence which can be an example for modern youth, especially for scientific youth are reduced. The study was carried out at the expense of budgetary
funds according to the state assignment of the Financial University No. 15841p-P8.

In paper the problem of reflection of a spherical sound wave from an elastic half -space with an adjacent inhomogeneous liquid layer is considered. It is assumed that a homogeneous isotropic elastic half-space is covered by an continuously-inhomogeneous of a plane liquid layer with an arbitrary law of inhomogeneity. A point source of harmonic sound waves is placed in an ideal homogeneous liquid bordering an inhomogeneous layer.
The analytical solution of the viewed problem is obtained on the basis of the solution of a similar problem for the case of a plane incident wave.
The acoustic pressure in a spherical wave is represented in integral form as a decomposition on a plane waves. The integrand expression turns out to be similar in form to the expression for pressure in a plane incident wave. Therefore, the pressure in a scattered wave in the case
of a spherical wave falling on a half-space with an inhomogeneous liquid layer is written as an integral, the integral expression of which is similar in form to the expression for the pressure in a scattered wave when a plane wave falls. For the determination of the wave field in an
inhomogeneous liquid layer the boundary value problem for a system of ordinary differential equations of the second order is built, the approximate analytical solution of which is obtained by the power series method.

The performance properties of many precision mechanical engineering products manufactured by plastic deformation methods depend significantly on the structural deformation damage of their material. In this regard, methods of mathematical modeling of the complex physical process of structural damage are essential for calculating and predicting reliable operational characteristics of these products. According to systematic experimental data, the damage of metals in large plastic deformations is mainly associated with the formation, growth and coalescence of pores. To formulate the defining relations and determine the material functions included in them, a geometric model of elementary volume (RVE) with stochastically distributed
mesoelements (ME) representing a material shell with sometimes is used. For step-by-step calculation of strain increment tensor components at RVE- and ME- levels, their initial (undeformed) and current (deformed) configurations are determined by the metric tensor.
Calculation of damage measures based on experimentation, determination and modeling of material functions of plastic dilatancy and deviator deformation of ME depending on deviator deformation of RVE in plastic compression experiments, is given.

Based on the developed method for determining the boundaries of the stress-strain state (VAT) regions and the coordinates of plasticity zones developing in the vicinity of pores in loaded powder products of SLM technology, a hypothesis is proposed and calculations are carried out confirming the influence of pore morphology in powder additive alloys on the anisotropy of their physico-mechanical properties. The influence of the external tensile stress and the possible pressure of gases in the pores is taken into account.
The calculation made it possible to clarify the place of origin, shape and coordinates of the boundary of the development of the plasticity zone (cracking) in the vicinity of a spherical pore, depending on the ratio of external stress and gas pressure in the pores.
The obtained expressions for estimating the size of the plasticity zone can be used to clarify the parameters of the kinetics of the destruction processes of products made of porous steels manufactured using SLM technology under conditions of their stress corrosion.

The method of observation and statistical analysis of the number and distribution of structural defects (discontinuities of various morphologies and non-metallic inclusions) in the volume of loaded samples of powder stainless and high-strength alloys of Fe-Cr-Ni, Fe-Cr-Ni-Mo systems manufactured according to additive technology SLM is described.
The task of assessing porosity from a computed tomography (CT) image is to determine the presence of elements (objects) in the image with certain individual characteristics. This characteristic is the brightness of the image elements. The simplest and most natural way
to detect an object/objects is to select a brightness threshold or threshold classification (thresholding). In the work, the Nobuyuki Otsu method, developed in 1979, was used for these purposes.
A comparison of the informative value of porosity results for the analysis of images obtained using X-ray computed tomography and metallographic analysis (optical, SEM) techniques is presented. The highest porosity content in the CT scanned sample was ∼0.61-0.82%. The pores in the samples of SLM alloys in both cases (optical microscopy and computed tomography) are unevenly distributed. The problems affecting the amount of information and quantitative
characteristics of stress concentrators recorded in objects are analyzed.
The prospects of using the Ots algorithm for processing CT images and estimating the porosity distribution in samples of additive manufacturing are shown, which made it possible to visualize in detail the internal pores in samples in 3D without their physical and chemical
destruction compared with metallographic preparation.

The splitting of rock massifs into blocks by cracks is considered. Taking as a basis a model in which cracks are systems of unlimited equidistant (i.e. parallel and equidistant) plane systems, the article examines the distribution of blocks by volumes and shapes and presents a method
that allows you to find the distribution of blocks not only by volume, as all previously developed methods, but also by other geometric parameters.

The paper studies the properties of the hyperbolic zeta function of diagonal two-dimensional unimodular lattices. A theorem on the analytic continuation of this function is proved.

The definition of a generalized parallelepipedal net does not provide a simple idea of how to construct it. The article proposes algorithms for constructing generalized parallelepipedal nets corresponding to integer lattices.

Let N be the set of natural numbers, Z_+ be the set of non-negative integers, C be the set of complex numbers, 𝐴(𝑈) be the set of analytic functions in the unit circle 𝑈 := {𝑧 ∈ C : |𝑧| < 1}, 𝐵_2 – be the Bergman spaces of functions 𝑓 ∈ 𝐴(𝑈), endowed with a finite norm 

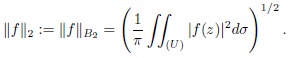For 𝑓 ∈ 𝐴(𝑈), we denote the usual derivative of order 𝑚 ∈ N by 𝑓(𝑚)(𝑧) and introduce a class of functions

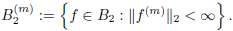Let 𝐸_(𝑛−1)(𝑓)_2 be the magnitude of the best approximation of function 𝑓 ∈ 𝐵_2 by complex algebraic polynomials of degree ≤ 𝑛 − 1. In this paper, a number of exact inequalities are found between the value of the best approximation of intermediate derivatives 𝐸__(𝑛−𝜈−1)(𝑓^(𝜈))_2 (𝜈 = 1, 2, · · · ,𝑚 − 1;𝑚 ≥ 2) and the best approximation 𝐸(_𝑛−𝑚−1)(𝑓^(𝑚))_2 of the highest derivative 𝑓(𝑚). Let 𝑊^(𝑚)_2 := 𝑊^(𝑚)_2 (𝑈) (𝑚 ∈ N) be a class of functions 𝑓 ∈ 𝐵^(𝑚)
2 for which ‖𝑓^(𝑚)‖_2 ≤ 1. In this paper is proved that for any 𝑛,𝑚 ∈ N, 𝜈 ∈ Z+, 𝑛 > 𝑚 ≥ 𝜈, the equality of takes place

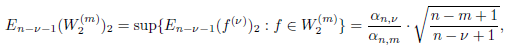and also, in the space 𝐵2 for functions 𝑓 ∈ 𝐵^(𝑚)_2 for all 1 ≤ 𝜈 ≤ 𝑚 − 1,𝑚 ≥ 2, an exact inequality of the Kolmogorov type

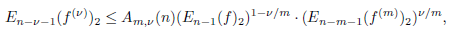is found, where the constant 𝐴𝑚,𝜈(𝑛) is explicitly written out. Some applications of the resulting inequality are given.

We prove here that at least one of the two 2-adic numbers which are the values at 𝑧 = 1 of the sums in Q_2 of the series

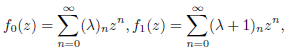where 𝜆 is a certain polyadic Liouville number. The series considered converge in any field Q_𝑝. We deal here with Q_2. The symbol (𝛾)𝑛 denotes Pochhammer symbol, i.e. (𝛾)0 = 1 , and for 𝑛 ≥ 1 we have (𝛾)_𝑛 = 𝛾(𝛾 + 1)...(𝛾 + 𝑛 − 1). The values of these series were also calculated at polyadic Liouville number. The canonic expansion of a polyadic number 𝜆 is of the form 

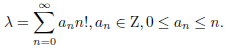This series converges in any field of 𝑝− adic numbers Q_𝑝 .
We call a polyadic number 𝜆 a polyadic Liouville number, if for any 𝑛 and 𝑃 there exists a positive integer 𝐴 such that for all primes 𝑝, satisfying 𝑝 ≤ 𝑃 the inequality

holds.
It was proved earlier that the Liouville polyadic number is transcendental in any field Q_𝑝.
In other words,the Liouville polyadic number is globally transcendental. It allowed to prove using some equality that there exists an infinite set of 𝑝−adic fields Q_𝑝 where at least one of
the numbers 𝑓_0(𝑧), 𝑓_1(𝑧). Here we prove the transcendence of values in the field Q_2.