Неравенство типа Колмогорова в пространстве Бергмана 𝐵2 и некоторые его приложения

Аннотация

Пусть N – множество натуральных чисел, Z+ – множество неотрицательных целых чисел, C – множество комплексных чисел, 𝐴(𝑈) – множество аналитических в единичном круге 𝑈 := {𝑧 ∈ C : |𝑧| < 1} функций, 𝐵2 – пространство Бергмана функций 𝑓 ∈ 𝐴(𝑈),
наделенных конечной нормой

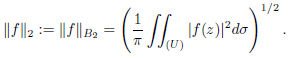
Для 𝑓 ∈ 𝐴(𝑈) обычную производную порядка 𝑚 ∈ N обозначим через 𝑓(𝑚)(𝑧) и введём класс функций

Пусть 𝐸_(𝑛−1)(𝑓)_2 – величина наилучшего приближения функции 𝑓 ∈ 𝐵2 комплексными алгебраическими полиномами степени ≤ 𝑛 − 1. В данной работе найден ряд точных неравенств между величиною наилучшего приближения промежуточных производных 𝐸_(𝑛−𝜈−1)(𝑓^(𝜈))_2 (𝜈 = 1, 2, · · · ,𝑚− 1;𝑚 ≥ 2) и наилучшего приближения 𝐸_(𝑛−𝑚−1)(𝑓^(𝑚))_2 старшей производной 𝑓^(𝑚).

Пусть 𝑊^(𝑚)_2 := 𝑊^(𝑚)_2 (𝑈) (𝑚 ∈ N)−класс функций 𝑓 ∈ 𝐵^(𝑚)_2 , для которых ‖𝑓^(𝑚)‖_2 ≤ 1.
В работе доказано, что при любых 𝑛,𝑚 ∈ N, 𝜈 ∈ Z+, 𝑛 > 𝑚 ≥ 𝜈 имеет место равенство

а также для функций 𝑓 ∈ 𝐵^(𝑚)_2 при всех 1 ≤ 𝜈 ≤ 𝑚−1,𝑚 ≥ 2 найдено точное неравенство типа Колмогорова

где постоянная 𝐴_(𝑚,𝜈)(𝑛) явно выписывается. Дано некоторые приложения полученного неравенства.