Article
The work proves that, under some additional conditions, every sufficiently large integer can be represented as the sum of two prime numbers and the square of a third prime number. A lower bound for the quantity of representation of a given integer in the specified form has also been proven.
In this paper we consider mutual information for a pair of random variables and find a third variable (condition) that maximise conditional mutual information of three of them.
A method for solving the Delsarte extremal problem 𝐴𝑠 for weighted designs is proposed. The value of 𝐴𝑠 is defined as the supremum of 𝑓(1) over the class of continuous nonnegative functions 𝑓 on [−1, 1] that can be represented by a Fourier–Jacobi expansion with a unit zero
coefficient and nonpositive coefficients starting from the (𝑠 + 1)th term. The main application of the problem 𝐴𝑠 lies in providing a lower bound for the number of nodes of weighted 𝑠-designs (or quadrature formulas, exact on a subspace of polynomials of degree at most 𝑠) in compact homogeneous Riemannian spaces of rank 1, where the zonal functions are Jacobi polynomials. The method for solving 𝐴𝑠 is based on convex an alysis and builds on the results of V.V. Arestov and A.G. Babenko for the case of spherical codes, as well as on specific cases developed by I.A. Martyanov and the author. The method involves several steps, including the formulation of a dual problem for the Stieltjes measure, proving the existence of the extremal function
and measure, deriving the duality relations, characterizing the extremal function and measure based on these relations, reducing the problem to a polynomial system of equations, and demonstrating the existence of a unique real analytic solution of the system in the vicinity of a numerical solution in the studied cases. This step is carried out by certifying the solution using the HomotopyContinuation.jl package, which implements the Krawczyk interval method. A uniform estimate for Jacobi polynomials of the Stieltjes–Bernstein type is also applied. Using this approach, two new Delsarte problems were solved as examples. Additionally, for the case corresponding to projective spaces, it is proven that the extremal function is a polynomial.
For the case corresponding to the sphere, this remains an open problem. These results are useful for the problem of discretizing the integral norm when estimating the number of nodes in discrete norms.
The paper provides answers to the following questions:
First, the question is in which case the harmonic numbers from the class (𝑀_s)^𝛼 do not fall into the lattice of linear comparison solutions corresponding to the parallelepipedal grid. As a result, a new object of research has appeared – the intersection of the lattice of linear comparison solutions corresponding to a parallelepipedal grid and a multidimensional mononoid defining a class of functions.
Secondly, what do the boundary functions of these classes look like for parallelepipedal grids. Here we did not get a simple finite form in the form of an expression from elementary functions, but only an expression in the form of series according to the general theory. The
estimation of the error of approximate integration on the class 𝑀𝛼
𝑠 is associated with the study of a new number-theoretic object – the hyperbolic zeta function of the intersection of the lattice of solutions of linear comparison and a multidimensional monoid defining a class of functions. Here it was possible to obtain an analogue of the enhanced Bakhvalov–Korobov theorem.
Finally, the third question is related to the fact that parallelepipedal grids are interpolationtype grids: what is the error of interpolation polynomials for valid parallelepipedal grids in the case of the monoid 𝑀𝑞,1. The answer here is as follows: interpolation formulas for
parallelepipedal grids are accurate only for some trigonometric polynomials, in which all harmonics fall into the complete system of deductions of the fundamental lattice by the sublattice of solutions of the corresponding linear comparison. In general, the error estimate is
similar to the estimates for the Korobov class.
In the article, by means of specially designed approximation grid nodes, the class of polynomials 𝐿𝑛(𝑧, 𝑢) of degree 𝑛 ⩾ 1 is determined, which deviate least from zero on the interval −1 ⩽ 𝑢 ⩽ 1, equal to zero at 𝑢 = −1. For polynomials 𝐿𝑛(𝑧, 𝑢) a connection with Chebyshev polynomials of the first kind is described; the 𝑛-point Chebyshev alternance was studied; extrema are found; exact expressions for the roots and coordinates of the maximum and minimum points are obtained; the formula of the senior coefficient is derived; a segment
is found where the polynomial increases monotonically and tends to +∞ as 𝑢 → +∞. Specific examples of the Chebyshev alternance of the second, third and fourth order are given.
We consider algebraic polynomials of degree n with real coefficients. When processing the input data, a uniform continuous rate of absolute error was used. The influence of input data error on the quality of approximation in the coefficient inverse problem for an algebraic polynomial with a prescribed lowest coefficient is studied. In the problem of minimizing the influence of the input data error, the objective function is described as an absolute condition number of the problem, equal to the value of the Lebesgue function. The graphical material shows the level of increase in the numerical value of the absolute condition number of the problem when the coordinates of the approximation grid nodes deviate from the optimal ones.
To minimize the influence of the input data error on the accuracy of calculating the coefficients of the studied algebraic polynomial, the location of the nodes of the approximation grid was specially designed. With the Chebyshev approximation, the connection of the nodes with the alternance points of the polynomials 𝐿𝑛(𝑧, 𝑢) by a linear function is obtained.
For 𝑛 ≥ 3, an asymptotic formula for the number of representations of a sufficiently large natural number 𝑁 in the form 𝑝_1 + 𝑝_2 + 𝑚^𝑛 = 𝑁, is obtained. Here 𝑝_1, 𝑝_2 are prime numbers, and 𝑚 is a natural number, satisfying the following conditions
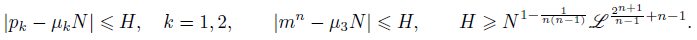
Сomputer science
The article is devoted to the emergence and first successes of a group of researchers in Moscow in the 1930 - 50-s who laid the foundations of the Soviet school of the history of mathematics, which received international recognition in the second half of the 20-th century. The article highlights the ideological reasons that put forward the history and philosophy of science in the category of the most important scientific disciplines in the early years of the young Soviet state.
The participation of the staff of the Section of Natural and Exact Sciences of the Communist Academy in the reorganization of the Moscow Mathematical Society in 1930 and their activities in creating lecture courses and seminars on the history and methodology of mathematics at Moscow University are traced.
This paper is aimed on comparison of two types of quasistatic linear elasticity problem approximate solutions. The problem of a multilayered composite rectangular plate bending is considered; the layers of the plate are supposed to be orthotropic, and orthotropy axes are supposed to be parallel to the sides of the plate; the edges of the plate are simply supported. The structural functions method is the main method considered in this paper: this method is in computing the displacements in the abovementioned inhomogeneous plate as a weighted sum of spatial derivatives of the displacements in a homogeneous plate of the same geometry under the same to the inhomogeneous one loadings – that homogeneous plate is called a concomitant one. The coefficients of that weighted sum are named structural functions. In this paper, we pass through all the necessary steps of the structural functions method and derive the formulae
for the structural functions of the first and the second order. Also, we present an approach to the choice of the concomitant body elastic characteristics, and compare it with one of the previous approaches. Approximate solutions of the above-stated problem via the structural
functions method of first and second order are numerically compared with the finite element method solutions (based on the 8-knot and 20-knot elements), and with well-known N. J. Pagano solution to the same problem in a three-dimensional statement.
The direct and inverse problems of sound transmission through a three-layer sandwich panel with elastic homogeneous outer layers and a core in the form of an elastic continuously inhomogeneous layer thickness are considered. It is assumed that the panel is in an ideal
compressible liquid, and the wave incident on it is plane and harmonic.
In the direct problem, with the well-known law of inhomogeneity of the core, wave fields in the sandwich panel and the half-spaces bordering it are determined. The velocity potentials of the sound waves reflected from the sandwich panel and transmission through it, as well as the displacement potentials of elastic waves excited in the outer layers of the panel, are in the form of decompositions according to Cartesian basic solutions of the Helmholtz equation. To determine
the displacement field in the core, a boundary value problem for a system of linear ordinary differential equations of the second order is obtained. The influence of the inhomogeneity of the core on the transmission of sound through the sandwich panel is numerically investigated.
In the inverse problem, the laws of inhomogeneity of the core are determined, ensuring minimal sound permeability of the sandwich panel. Based on the solution of the direct problem, a functional is constructed, defined on a class of linear functions describing the mechanical parameters of the core and expressing the average sound permeability coefficient of the sandwich panel in a given frequency range. The minimization of the functionality is carried out using an
algorithm based on a combination of random search and coordinate descent methods.
In paper the general formulation of solid mechanics boundary problems for elasto-plastic shells is presented. The approach to numerical modeling of shells in the MITC formulation on small strains in the context of the finite element method, which was implemented in
the local strength analysis software CAE Fidesys, is considered. The development specific is to take into account the effects of plastic flow in the calculation of shells by implementing algorithms of integration over the thickness of the shell. Thus, it is possible to use the Huber-
Mises yeld criterion directly in contrast to a number of studies, in which the condition for achieving plasticity is written in the resultants. The Newton-Raphson method was applied to solve nonlinear systems of equations. In paper the number of key aspects of the corresponding
mathematical model is reviewed and presented. The algorithms implementation is evaluated by comparing the results obtained in the context of algorithms implementation in CAE Fidesys for elasto-plastic circular plate loading problems with similar results in other CAE programs. In particular, the problem which is appropriate to the Lame problem under plane-stress conditions and the plate bending problem are considered.
The stress-strain state in the vicinity of a cavity formed in a pre-strained body made of elastic-plastic material is calculated for the case of step-by-step cavity growth in several stages.
The problem is solved in a quasi-static formulation for finite strains taking into account their redistribution after each stage of deformation. It is assumed that the transition of material to a plastic state occurs in accordance with the von Mises plasticity condition, and plastic deformation of the material is described by the associated law of plastic flow. The problem is formulated and solved based on the theory of multiple superposition of large strains. A general algorithm for solving the problem within the framework of this theory is presented. The finite element method and the spectral element method are used for the solution. The methods and algorithms implemented in the Fidesys engineering strength analysis system and software modules included in this system were used in the solution. Model calculations are performed for the case of plane deformation of a square body with a central elliptical (at the time of formation) cavity, the growth of which occurs in several stages according to a predetermined law. Graphs of stress distribution in the body are given. The influence of plastic properties of the material and multi-stage deformation on the stress-strain state is investigated.
A numerical solution to the problem of the stress-strain state in a body made of an elastoplastic material with the sequential formation of several cavities in it after preliminary loading at finite deformations has been obtained and studied. To model plasticity, the Mises condition and the law of plastic flow associated with this condition were used. A general mechanical formulation of the problem is given based on the theory of repeated superposition of large deformations. The general solution algorithm is outlined. To solve the problem, we used the finite element method and its modification — the spectral element method. The solution was obtained using methods and algorithms of the engineering strength analysis system. Some results of numerical calculations are presented for the plane static problem of stress concentration in the vicinity of three elliptical cavities formed in a body of square cross-section in the case of plane strain. Effects caused by plasticity, geometric nonlinearity, and redistribution of finite
deformations were studied. The results were compared for cases of sequential and simultaneous formation of cavities.
The article has put in order Euler iconography from his lifetime images to the 20th century. Hypothesis being discussed: Euler self-portrait in his notebook.
This paper shows the possibilities of applying similarity and dimensionality methods for mathematical modelling of tribosystem — a friction pair in which, in addition to solid surfaces, there is a multi-component lubricant.
Multifactorial tribological phenomena often cannot be described using formal laws, the models we propose allow us to carry out studies of such processes. The essence of the method is that the dependent variable — in this case, stationary wear of friction surfaces — is represented as a set of independent (or weakly dependent) variables.
Two basic theorems of the method of dimension analysis were applied to the general model: the theorem on the dimensionality of quantities in the system of basic dimensions of mechanics and Buckingham’s theorem on finding the number of dimensionless complexes.
The possibility of reducing the number of model variables and forming a system of new, simpler models, which allow to describe the process explicitly, was shown.
This article is devoted to the numerical estimation of the effective thermal conductivity coefficients of heterogeneous media. An estimation algorithm is described, modified for the non-linear case (when the thermal properties of the material components depend on the temperature). Using the Fidesys CAE system, linear calculations are performed to estimate the effective thermal conductivity coefficients of construction heat-insulating composites made of polymer reinforced with hollow glass microspheres. The cases of simple cubic packing of filler particles and their random distribution in the matrix are investigated. The modified algorithm is implemented as a research software module for solving non-linear problems of estimating effective thermal conductivity. Using it, model problems of estimating non-linear effective thermal conductivity for orthogonally reinforced and particle-reinforced composites are solved. The configuration of an orthogonally reinforced composite is revealed, the effective
thermal conductivity of which does not depend on temperature. A significantly non-monotonic dependence of the effective thermal conductivity on temperature is obtained for a particlereinforced
composite.
Краткие сообщения
In 2013–2015 it was shown that for any purely real algebraic irrationality 𝛼, starting from some place, all residual fractions in the expansion of 𝛼 into a continued fraction will appear to be the reduced algebraic irrationalities.
We construct the examples of purely real algebraic irrationalities 𝛼 for which this number of the residual fraction is arbitrarily large.
For an arbitrary odd-degree polynomial 𝑓 over an arbitrary field of algebraic numbers K, the class of always quasiperiodic elements in K((𝑥)) of the form 𝑣+𝑤√𝑓/𝑢 , where 𝑣,𝑤, 𝑢 ∈ K[𝑥], in the hyperelliptic field K(𝑥)(√𝑓), has been determined. This class is characterized by certain relationships involving the polynomials 𝑢, 𝑣,𝑤, and 𝑓, as well as their degrees. The class is guaranteed to be nonempty if at least one quasiperiodic element exists in the hyperelliptic field.
Furthermore, a specific subclass of always periodic elements has been identified within this broader class.
In this paper, we aim to derive a quantitative version of a problem on the size of a set of fractions 𝐴/𝐴, in the case where 𝐴 is a given finite set of natural numbers lying in the interval [1, 𝑛], having positive asymptotic density 𝛼 > 0 as 𝑛 → ∞.






























