Статьи
В работе доказано, что при некоторых дополнительных условиях каждое достаточно большое целое число представимо в виде суммы двух простых и квадрата третьего простого числа. А также доказана оценка снизу для количества представлений данного целого
числа в указанном виде.
В этой статье мы рассматриваем взаимную информацию для пары случайных величин и находим третью переменную (условие), которая максимизирует условную взаимную информацию трех из них.
Доказано равенство коэффициентов интерполяционного многочлена по параллелепипедальной сетке для многомерной функции коэффициентам интерполяционного многочлена
по равномерной сетке для одномерной функции, для получения которых можно применить быстрое преобразование Фурье по различным схемам.
Предложен метод решения экстремальной задачи Дельсарта 𝐴𝑠 для взвешенных дизайнов. Величина 𝐴𝑠 равна верхней грани 𝑓(1) на классе непрерывных неотрицательных на [−1, 1] функций 𝑓, представимых разложением Фурье–Якоби с единичным нулевым коэффициентом и неположительными коэффициентами, начиная с номера 𝑠 + 1. Основное приложение задачи 𝐴𝑠 заключается в оценке снизу числа узлов взвешенных 𝑠-дизайнов (или квадратурных формул, точных на подпространстве полиномов степени не выше 𝑠) на компактных однородных римановых пространствах ранга 1, где зональными функциями являются многочлены Якоби. Метод решения задачи 𝐴𝑠 базируется на выпуклом анализе и следует результатам В.В. Арестова и А.Г. Бабенко для случая сферических кодов, а также частным вариантам, полученным И.А. Мартьяновым и автором. Метод состоит из нескольких шагов, включая формулировку двойственной задачи для меры Стилтьеса, доказательство существования экстремальной функции и меры, выписывание соотношений двойственности, характеризация на их основе экстремальных функции и меры, сведение задачи к полиномиальной системе уравнений, доказательство в конкретных случаях существования в окрестности численного решения единственного действительного аналитического решения системы. Этот шаг делается сертификацией решения при помощи пакета
HomotopyContinuation.jl, где реализован интервальный метод Кравчука. Также применяется равномерная оценка многочленов Якоби типа Стилтьеса–Бернштейна. Описанным способом в качестве примера было решено две новых задачи Дельсарта. Также в случае, отвечающим проективным пространствам доказано, что экстремальная функция является многочленом. Для случая, отвечающего сфере, это пока открытая проблема. Данные результаты полезны в проблеме дискретизации интегральной нормы при оценке числа узлов дискретных норм.
В работе получены ответы на следующие вопросы.
Во-первых, вопрос о том, в каком случае номера гармоник из класса (𝑀_𝑠)^𝛼 не попадают в решётку решений линейного сравнения, соответствующего параллелепипедальной сетке. В
результате появился новый объект исследования – пересечение решётки решений линейного сравнения, соответствующего параллелепипедальной сетке, и многомерного мононоида,
задающего класс функций.
Во-вторых, как выглядят граничные функции этих классов для параллелепипедальных сеток. Здесь не получилось простого конечного вида в виде выражения от элементарных функций, а только выражение в виде рядов согласно общей теории. Оценка погрешности приближенного интегрирования на классе 𝑀𝛼
𝑠 связана с изучением нового теоретико-числового объекта – гиперболической дзета-функции пересечения решётки решений линейного сравнения и многомерного моноида, задающего класс функций. Здесь удалось получить аналог усиленной теоремы Бахвалова — Коробова.
Наконец, третий вопрос, связанный с тем фактом, что параллелепипедальные сетки — это сетки интерполяционного типа: какова погрешность интерполяционных многочленов
для допустимых параллелепипедальных сеток в случае моноида 𝑀𝑞,1. Здесь ответ получился следующий: интерполяционные формулы по параллелепипедальным сеткам точны только для некоторых тригонометрических многочленов, у которых все гармоники попадают в полную систему вычетов фундаментальной решётки по подрешётки решений соответствующего линейного сравнения. В общем случае оценка погрешности аналогична
оценкам для класса Коробова.
В статье посредством специально сконструированных узлов сетки аппроксимации определяется класс многочленов 𝐿𝑛(𝑧, 𝑢) степени 𝑛 ⩾ 1, наименее уклоняющихся от нуля на отрезке – −1 ⩽ 𝑢 ⩽ 1, равных нулю при 𝑢 = −1. Для многочленов 𝐿𝑛(𝑧, 𝑢): описана связь
с многочленами Чебышева первого рода; изучен 𝑛-точечный альтернанс; найдены экстремумы; получены точные выражения корней и координат точек максимума и минимума; выведена формула старшего коэффициента; найден отрезок, где многочлен монотонно возрастает и стремится к +∞ при 𝑢 → +∞. Приведены конкретные примеры альтернанса второго, третьего и четвертого порядка. Мы рассматриваем алгебраические многочлены
степени 𝑛 с действительными коэффициентами. При обработке входных данных использована равномерная непрерывная норма абсолютной погрешности. Исследовано влияние погрешности входных данных на качество аппроксимации в коэффициентной обратной задаче для алгебраического многочлена с предписанным младшим коэффициентом. В задаче минимизации влияния погрешности входных данных целевая функция описана в виде абсолютного числа обусловленности задачи, равного значению функции Лебега. На графическом материале показано увеличение численного значения абсолютного числа обусловленности задачи при отклонении координат узлов сетки аппроксимации от оптимальных.
Для минимизации влияния погрешности входных данных на точность вычисления коэффициентов исследуемого алгебраического многочлена специально сконструировано
расположение узлов сетки аппроксимации. При чебышевской аппроксимации получена связь узлов с точками альтернанса многочленов 𝐿𝑛(𝑧, 𝑢) линейной функцией.
При 𝑛 ⩾ 3 получена асимптотическая формула для количества представлений достаточно большого натурального 𝑁 в виде 𝑝_1 + 𝑝_2 + 𝑚:𝑛 = 𝑁, где 𝑝_1, 𝑝_2 — простые числа, 𝑚 — натуральное число, удовлетворяющие условиям
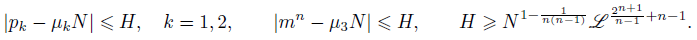
История математики и приложений
Статья посвящена появлению и первым успехам в 1930–50-е годы в Москве группы исследователей, заложивших основы советской историко-математической школы, получившей международное признание во второй половине ХХ столетия. Освещаются идеологические причины, выдвинувшие в первые годы молодого советского государства историю и философию науки в разряд важнейших научных дисциплин. Прослежены участие сотрудников секции естественных и точных наук Коммунистической академии в реорганизации Московского математического общества в 1930 г. и их деятельность по созданию в Московском университете лекционных курсов и семинаров по истории и методологии математики.
Цель данной статьи – сопоставление приближенных решений одной квазистатической задачи теории упругости для слоистого материала. Рассматриваются приближенные решения, построенные по методу структурных функций В. И. Горбачева с вариацией конкретных параметров метода, а также приближенные решения, построенные методом конечных
элементов. В качестве тестовой выбрана задача о нагружении трехслойной прямоугольной пластины, слои которой ортотропны в осях координат, параллельных сторонам пластины; боковые грани пластины закреплены так, что на каждой из граней возможны только перемещения в направлении, нормальном к этой грани. В статье приводится процедура построения приближенных решений указанной задачи при помощи метода структурных функций. Данный метод для указанной задачи состоит в вычислении перемещений в неоднородной пластине как частичной суммы ряда по производным решения так называемой сопутствующей задачи – иначе говоря, по перемещениям в однородной пластине аналогичной геометрии, закрепленной и нагруженной так же, как неоднородная пластина. Коэффициенты этой частичной суммы называются структурными функциями, а порядок производных в слагаемых, входящих в частичную сумму, называют порядком метода структурных функций. В статье приведены приближенные решения указанной задачи,
построенные методом структурных функций первого и второго порядка, а также предложен новый вариант выбора упругих свойств сопутствующего тела. Для двух тестовых пластин – симметричной и не симметричной относительно серединной плоскости – проведено численное сравнение приближений, построенных по методу структурных функций, конечноэлементых приближений, основанных на использовании восьмиузловых и двадцатиузловых конечных элементов, и решения по методу N. J. Pagano. Показано, что даже для пластин с большим отношением толщины к длине (1/4) метод структурных функций дает удовлетворительное приближение, а повышение порядка метода повышает качество приближения.
Рассматриваются прямая и обратная задачи о прохождении звука через трехслойную сэндвич-панель с упругими однородными наружными слоями и заполнителем в виде упругого непрерывно-неоднородного по толщине слоя. Полагается, что панель находится в идеальной сжимаемой жидкости, а падающая на нее волна является плоской и гармонической.
В прямой задаче при известном законе неоднородности заполнителя определяются волновые поля в сэндвич-панели и граничащих с ней полупространствах. Потенциалы скоростей отраженной от сэндвич-панели и прошедшей через нее звуковых волн, а также потенциалы смещений упругих волн, возбужденных в наружных слоях панели, находятся в виде разложений по декартовым базисным решениям уравнения Гельмгольца. Для определения поля смещений в заполнителе получена краевая задача для системы линейных обыкновенных дифференциальных уравнений второго порядка. Численно исследовано влияние
неоднородности заполнителя на прохождение звука через сэндвич-панель.
В обратной задаче определяются законы неоднородности заполнителя, обеспечивающие минимальную звукопроницаемость сэндвич-панели. На основе решения прямой задачи построен функционал, определенный на классе линейных функций, описывающих механические параметры заполнителя и выражающий осредненный коэффициент звукопроницаемости сэндвич-панели в заданном диапазоне частот. Минимизация функционала осуществляется с помощью алгоритма, основанного на комбинации методов случайного поиска и покоординатного спуска.
В статье приведена общая постановка краевых задач механики деформируемого твердого тела для упруго-пластических оболочек. Рассмотрен подход к численному моделированию оболочек в MITC формулировке при малых деформациях в рамках метода конечных элементов, который был реализован в отечественном пакете прочностного анализа CAE Fidesys. Особенностью разработки является учет эффектов пластического течения при расчете оболочек путем реализации алгоритмов интегрирования по толщине оболочки. Таким образом, появляется возможность использования напрямую критерия пластичности Губера-Мизеса в отличие от ряда исследований, в которых условие достижения пластичности записано в результантах. Для решения нелинейных систем уравнений применен метод Ньютона-Раффсона. В работе рассмотрен и приведен ряд ключевых аспектов соответствующей математической модели. Произведена оценка качества реализации алгоритмов посредством сравнения результатов, полученных в CAE Fidesys, с аналогичными результатами в других CAE пакетах для задач о нагружении упруго-пластических кольцевых пластин. В частности, рассмотрена задача, соответствующая задаче Ламе в условиях
плоско-напряженного состояния, а также задача об изгибе пластинки.
Выполнен расчет напряженно-деформированного состояния в окрестности полости, образованной в предварительно деформированном теле из упругопластического материала,
для случая пошагового роста полости в несколько этапов. Задача решается в квазистатической постановке при конечных деформациях с учетом их перераспределения после каждого этапа деформирования. Предполагается, что переход материала в пластическое состояние происходит в соответствии с условием пластичности Мизеса, а пластическое деформирование материала описывается ассоциированным законом пластического течения.
Постановка и решение задачи осуществляются на основе теории многократного наложения больших деформаций. Приведен общий алгоритм решения задачи в рамках этой теории.
Для решения используются метод конечных элементов и метод спектральных элементов.
При решении использованы методы и алгоритмы, реализованные в системе инженерного прочностного анализа Фидесис, и программные модули, входящие в эту систему. Модельные расчеты выполнены для случая плоской деформации тела квадратного сечения с центральной эллиптической (в момент образования) полостью, рост которой происходит в несколько этапов по заранее заданному закону. Приведены графики распределения напряжений в теле. Исследуется влияние пластических свойств материала и многоэтапности
деформирования на напряженно-деформированное состояние.
Получено и исследовано численное решение задачи о напряженно-деформированном состоянии в теле из упругопластического материала при последовательном образовании в нем нескольких полостей после предварительного нагружения при конечных деформациях. Для моделирования пластичности использовано условие Мизеса и ассоциированный с
этим условием закон пластического течения. Приведена общая механическая постановка задачи на основе теории многократного наложения больших деформаций. Изложен общий алгоритм решения. Для решения использован метод конечных элементов и его модификация — метод спектральных элементов. Решение получено с использованием методов и алгоритмов системы инженерного прочностного анализа. Приведены некоторые результаты численных расчетов для плоской статической задачи о концентрации напряжений в окрестности трех эллиптических полостей, образованных в теле квадратного сечения, в случае
плоской деформации. Исследованы эффекты, обусловленные пластичностью, геометрической нелинейностью, перераспределением конечных деформаций. Выполнено сравнение результатов для случаев последовательного и одновременного образования полостей.
В статье систематизирована иконография Эйлера от его прижизненных изображений до XX в. Рассказано о новой находке: автопортрете Эйлера в его записной книжке.
В данной работе показаны возможности применения методов подобия и размерностей для математического моделирования трибосистемы — пары трения, в которой, помимо твердых поверхностей, присутствует еще и многокомпонентный смазочный материал.
Многофакторные трибологические явления зачастую невозможно описать при помощи формальных законов; предложенные нами модели позволяют проводить исследования
таких процессов.
Суть метода заключается в том, что зависимая величина — в данном случае стационарный износ поверхностей трения — представляется в виде набора независимых (или
слабозависимых) друг от друга переменных. К общей модели были применены две основные теоремы метода анализа размерностей: теорема о размерности величин в системе основных размерностей механики и теорема Букингема — о поиске числа безразмерных комплексов.
Показана возможность редукции числа переменных модели и формирование системы новых, более простых моделей, которые позволяют явно описывать процесс.
Статья посвящена численной оценке эффективных коэффициентов теплопроводности гетерогенных сред. Описан алгоритм такой оценки, модифицированный для нелинейного случая: когда тепловые свойства компонентов среды зависят от температуры. С помощью программного комплекса «Фидесис» проведены линейные расчёты оценки эффективных коэффициентов теплопроводности строительных теплоизолирующих композитов из полимера, армированного полыми стеклянными микросферами. Исследованы случаи простой кубической упаковки частиц наполнителя и случайного их распределения в матрице. Модифицированный алгоритм реализован в виде исследовательского программного модуля для решения нелинейных задач оценки эффективной теплопроводности. С его помощью решены модельные задачи оценки нелинейной эффективной теплопроводности для ортогонально армированного и дисперсно армированного композитов. Подобрана конфигурация ортогонально армированного композита, эффективная теплопроводность которого не зависит от температуры. Выявлен существенно немонотонный характер зависимости эффективной теплопроводности дисперсно армированного композита от температуры.
Краткие сообщения
В 2013–2015 гг. было показано, что для любой чисто-вещественной алгебраической иррациональности 𝛼, начиная с некоторого места, все остаточные дроби в разложении 𝛼 в
цепную дробь будут приведёнными алгебраическими иррациональностями.
В работе построены примеры чисто-вещественных алгебраических иррациональностей 𝛼, для которых это номер остаточной дроби может быть сколь угодно большим.
В случае произвольной нечетной степени многочлена 𝑓 над произвольным полем алгебраических чисел 𝐾 был получен класс всегда квазипериодических в K((𝑥)) элементов 𝑣+𝑤√𝑓/𝑢 для 𝑣,𝑤, 𝑢 ∈ K[𝑥] гиперэллиптического поля K(𝑥)(√𝑓), задаваемый только соотношениями на многочлены 𝑢, 𝑣,𝑤, 𝑓 и их степени. Этот класс не пуст при наличии в гиперэллиптическом поле хотя бы одного квазипериодического элемента. В классе был выделен подкласс заведомо периодических элементов.
В настоящей статье мы задаемся целью вывести количественную версию одной задачи о размере множества дробей 𝐴/𝐴 в случае, когда 𝐴 — заданное конечное множество натуральных чисел лежащее в интервале [1, 𝑛], имеющее положительную асимптотическую плотность 𝛼 > 0 при 𝑛 → ∞.






























