Since 2012, in harmonic analysis on the line with a power-law weight, the two-parameter (𝑘, 𝑎)-generalized Fourier transform proposed by S. Ben Sa¨ıd, T. Kobayashi, B. Orsted has been intensively studied. It generalizes the Dunkl transform depending on only one parameter 𝑘 ⩾ 0.
Together with an increase in the variety of unitary transforms, the presence of a parameter 𝑎 > 0 for 𝑎 ̸= 2 leads to the appearance of deformation properties, for example, for functions from the Schwartz space, the generalized Fourier transform may not be infinitely differentiable or rapidly decreasing at infinity. The fast decay is preserved only for the sequence 𝑎 = 2/𝑛, 𝑛 ∈ N. Some change of variable in this case also improves other properties of the generalized
Fourier transform. The generalized Dunkl transform obtained after changing the variable at 𝑎 = 2/(2𝑟 + 1), 𝑟 ∈ Z+ is devoid of deformation properties and, to a large extent, has already been studied. In this paper, we study the generalized Hankel transform obtained after a change of variable for 𝑎 = 1/𝑟, 𝑟 ∈ N. An invariant subspace of functions rapidly decreasing at infinity is described for it, and a differential-difference operator is found for which the kernel
of the generalized Hankel transform is an eigenfunction. On the basis of a new multiplication theorem for the Bessel functions Boubatra–Negzaoui–Sifi, two generalized translation operators are constructed, and their 𝐿𝑝-boundedness and positivity are investigated. A simple proof is given for the multiplication theorem. Two convolutions are defined for which Young’s theorems are proved. With the help of convolutions, generalized means are defined, for which sufficient
conditions for 𝐿𝑝-convergence and convergence almost everywhere are proposed. Generalized analogs of the Gauss-Weierstrass, Poisson and Bochner–Riesz means are investigated.

In this paper we consider the problem of partial hedging studied in [20]. In this problem, the risk of shortfall is estimated using a robust convex loss functional 𝐿(·). In our work, we formulate a dual problem different from the dual problem in [20], we prove the absence of a
duality gap, and also the existence of a solution to the primal and dual problems. In addition, we obtain the results of [20] under weaker assumptions using an approach related to the application of theorems of convex analysis.

We construct an example of a pair of (2-dimensional) 8-vertex simplicial toroidal polyhedra (each polyhedron without self-intersection) with same 1-dimensional skeleton in (Euclidean) 3-space, which do not have a single common 2-face, and the union of the 2-skeletons of these two polyhedra gives a geometric realization of the 2-skeleton of the 4-dimensional hyperoctahedron in 3-space. Also, we construct an example of a pair of 6-vertex simplicial polyhedral projective planes with the same 1-skeleton in 4-space, which do not have a single common 2-face, and the union of these projective planes gives a geometric realization of the 2-skeleton of the 5-
hypertetrahedron in 4-space. Finally, it is shown how to imagine, figuratively, the atoms in the molecule of methane CH4 “linked” by a pair of internally disjoint spanning polyhedral M¨obius strips.

We consider the problem of topological classification of mutual dispositions in the real
projective plane of two 𝑀-curves of degree 4. We study arrangements which are satisfact to the maximality condition (the oval of one of these curves has 16 pairwise different common points with the oval of the other of them) and some combinatorial condition to select a special type of such arrangements. Pairwise different topological models of arrangements of this type are listed, which satisfy the known facts about the topology of nonsingular curves and the topological consequences of Bezout’s theorem. There are 564 such models. We proved that 558 models cannot be realized by curves of degree 8. The remaining 6 models were constructed by us. Proofs of non-realizability are carried out by Orevkov’s method based on the theory of braids and links.

An asymptotic formula is obtained for the number of representations of a sufficiently large natural 𝑁 as a sum of nine cubes of natural numbers 𝑥𝑖, 𝑖 = 1, 9, satisfying the conditions 

$$|(𝑥_𝑖)^3− 𝜇𝑖𝑁| ⩽ 𝐻, 𝜇1 + . . . + 𝜇9 = 1 𝐻 ⩾ 𝑁^)1−(1/30)+𝜀), $$ 

where 𝜇1, . . . , 𝜇9 — positive fixed numbers. This result is a strengthening of E.M.Wright’s theorem.

The paper provides an overview of the results of the Tula School of Number Theory on the following issues interpolation of periodic functions of many variables defined in the nodes of a generalized parallelepipedal grid of an integer lattice, and by numerical integration algorithms with a stopping rule.
The necessary facts and notations are given in Section 2, which consists of 6 subsections: 2.1.
From the geometry of numbers; 2.2. Trigonometric sums of grids and lattices; 2.3. Inequalities for
renormalization on the space (𝐸_𝑠)^a ; 2.4. Interpolation formulas for the generalized parallelepipedal grid of an integer lattice; 2.5. Properties of the interpolation operator; 2.6. Estimates of the interpolation error. These subsections, along with the known facts and definitions obtained earlier at the Tula School of Number Theory, contain new concepts and facts related to interpolation on shifted parallelepipedal grids.
The following section 3. Algorithms of approximate integration and interpolation with the stopping rule contains new definitions related to the transfer of the concept of a concentric algorithm of approximate integration to the case of a multiplicative, concentric algorithm of
approximate interpolation.
The paper investigates new issues of approximate interpolation with stopping rules. In the 4th section, the most important and interesting case of nested sequences of parallelepipedal grids is considered for practical implementation. An estimate of the norm of the difference between two interpolation operators on a lattice and a sublattice was obtained, which made it possible to take the maximum of the modulus of the difference of these operators at the points of a larger parallelepipedal grid as the stopping rule of the concentric algorithm for approximate interpolation of periodic functions. In conclusion, the task for further research is formulated.

In this paper, projective invariants of cubic curves with a node or an acnode are obtained. It is proved that on the projective plane every two inflection points of a cubic curve with a node (acnode) are in an equianharmonic ratio with the points of tangents of the given curve at its node (acnode) located on the line containing these inflection points. And every three inflection
points of such a curve are in a quasi-anharmonic ratio with the point on tangent of this curve at its node (acnode) located on the line containing these inflection points.
It is established that in the projective plane any two crunodal (acnodal) cubics are projectively equivalent.
It is proved that four lines containing the node (acnode) of a cubic, namely: the line of the inflection points, the tangent and pseudotangent to the curve at the inflection point, the tangent to the curve at the point conjugate to the inflection point, are in a constant cross ratio equal to −3. Based on this fact, a number of properties of cubic curves with a node (acnode) in the Euclidean plane 𝐸2 are substantiated. Let us present some of the proved properties, denoting the cubic curve by the symbol 𝜎, and its node or acnode by the symbol 𝐼.

1. If the tangents of 𝜎 at an acnode 𝐼 pass through circle points of the plane 𝐸2, then the angle between any two lines, each of which connects the point 𝐼 with the inflection point of this curve, is equal to 𝜋/3.

2. The pseudotangent at the point 𝐼 divides the strip between the parallel tangents of 𝜎 passing through 𝐼, in the ratio of three to one, counting from the tangent of 𝜎 at the conjugate point with 𝐼, if and only if, when the line of the inflection points of 𝜎 coincides with the absolute line of the plane 𝐸2.

3. The tangent of 𝜎 at the conjugate point with 𝐼 divides the strip between the mutually parallel pseudotangents at the point 𝐼 and the line of the inflection points of 𝜎 in the ratio of three to one, counting from the pseudotangent, if and only if, when the tangent line of 𝜎 at the point 𝐼 coincides with the absolute line of the plane 𝐸2.

4. The line of the inflection points of the curve 𝜎 divides the strip between the parallel tangents to 𝜎 passing through 𝐼 in the ratio of three to one, counting from the tangent line of 𝜎 at the point 𝐼, if and only if when the pseudotangent of the curve 𝜎 at the point 𝐼 coincides with the absolute line of the plane 𝐸2.

5. The tangent of the curve 𝜎 at the point 𝐼 divides the strip between the line of inflection points and the parallel to it pseudotangent of 𝜎 at 𝐼 in the ratio of three to one, counting from the line inflection points, if and only if the tangent of the curve 𝜎 at the conjugate point with 𝐼 coincides with the absolute line of the plane 𝐸2.

Several extremal problems on the best mean-square approximation of the functions 𝑓, on a semiaxis with a power-law weight are solved in the paper, which can be applied in solving various problems. Exact Jackson–Stechkin-type inequalities are obtained for some classes of functions in which the values of the best approximations are estimated from above in terms of 𝑘-th order Hankel moduli of smoothness.

The paper investigates upper bounds on the period length of functional continued fractions for key elements of hyperelliptic fields over number fields. In the case when the hyperelliptic field is given by a polynomial of odd degree, the finite period length is trivially estimated from above twice the power of the fundamental 𝑆-unit. A more interesting and complicated case is when the hyperelliptic field is given by a polynomial of even degree. In 2019 V.P. Platonov and
G.V. Fedorov for hyperelliptic fields ℒ = Q(𝑥)(√𝑓), deg 𝑓 = 2𝑔 +2, over the field Q of rational numbers the exact interval of values 𝑠 ∈ Z is found such that the continued fractions of elements of the form
√𝑓/𝑥𝑠 ∈ ℒ∖Q(𝑥) are periodic. In this article, we find a generalization of this result for an arbitrary field as a field of constants. Based on this result, sharp upper estimates for the lengths of the periods are found functional continued fractions of elements of hyperelliptic fields over number fields 𝐾, depending only on the genus 𝑔 of the hyperelliptic field, the degree of extension 𝑘 = [𝐾 : Q] and order 𝑚 of the Jacobian torsion subgroup of the corresponding hyperelliptic curve.

The detection of a sufficient number of tensor invariants (and not only the first integrals), as [13, 14, 45] is known, allows integrating a system of differential equations. For example, the presence of an invariant differential form of the phase volume makes it possible to reduce the
number of required first integrals. As you know, this fact is natural for conservative systems.
For systems with attracting or repelling limit sets, not only some first integrals, but also the coefficients of the available invariant differential forms should, generally speaking, include transcendental (i.e. having essentially singular points, in the sense of complex analysis) functions
(see also [1, 23, 24]).
We briefly give examples of frequently occurring tensor invariants. Scalar invariants are the first integrals of the system under consideration. Invariant vector fields are symmetry fields for
a given system (they commute with the vector field of the system under consideration). The phase flows of systems of differential equations generated by these fields translate the solutions of the system in question into solutions of the same system. Invariant external differential forms (which is mainly carried out in this paper) generate integral invariants of the system under consideration. At the same time, the vector field of the system under consideration itself is one of the invariants (a trivial invariant). Knowledge of tensor invariants of the system of differential equations under consideration facilitates both its integration and qualitative research. Our approach consists in the fact that in order to accurately integrate an autonomous system of 𝑛 differential equations, in addition to the mentioned trivial invariant, it is necessary to know 𝑛 − 1 independent tensor invariants.
In this paper, we present tensor invariants (differential forms) for homogeneous dynamical systems on the tangent bundles of smooth four-dimensional manifolds and demonstrate the connection between the availability of these invariants and the existence of a complete set of first integrals, which is necessary for integrating of geodesic, potential, and dissipative systems.

The main aim of this manuscript is to work on the application part of CVMS. In this work we have demonstrated some common fixed results and then we deal primarily with two parts of applications,
part(I) Complex valued version of existence and common solution for second order nonlinear boundary value problem using greens function,

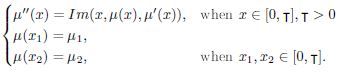
part(II) Application of fixed point results for multivalued mapping in setting of CVMS without using notion of continuity. Eventually several equivalent results and examples are presented to sustain our Main result.

Let 𝑎1, . . . , 𝑎𝑑 be natural numbers satisfying condition 𝑎1 ≥ 𝑎2 ≥ . . . ≥ 𝑎𝑑−1 ≥ 𝑎𝑑 = 1.
Define sequence {𝑇𝑛} using the linear recurrent relation 𝑇𝑛 = 𝑎1𝑇𝑛−1 + 𝑎2𝑇𝑛−2 + . . . + 𝑎𝑑𝑇𝑛−𝑑 and initial conditions 𝑇0 = 1, 𝑇𝑛 = 1 + 𝑎1𝑇𝑛−1 + 𝑎2𝑇𝑛−2 + . . . + 𝑎𝑛𝑇0 for 𝑛 < 𝑑. Let N(𝑤) be a set of natural numbers for which the greedy expansion on the linear recurrent sequence {𝑇𝑛} ends with some word 𝑤. Here 𝑤 is chosen in such a way that so that the set N(𝑤) is non-empty.
We study the problem about the number 𝑟𝑘(𝑁) of representations of a natural number 𝑁 in as the sum of 𝑘 terms from N(𝑤).
Using the previously obtained description of the sets N(𝑤) in terms of shifts of tori of dimension 𝑑 − 1, an asymptotic formula for the number of representations 𝑟𝑘(𝑁) is obtained, and also found upper bounds for the number of representations.
Conditions on 𝑘 that ensure the existence of considered representations for all sufficiently large natural numbers 𝑁 are found. In particular, such representations exist if 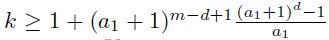, where 𝑚 is the length of the fixed end 𝑤 of the greedy expansion.
In addition, an asymptotic formula is obtained for the average number of representations.
In conclusion, several unsolved problems are formulated.

In this paper for the expension of real numbers on Fibonacci sequence theorems on the uniform distribution of remainders for almost of all real numbers in the sense of Lebesgue’s measure. the conclusion of this theorem is based on theWeyl’s criteria of the uniform distribution
of a sequence modulo unit and on the lemma.

The work is devoted to the evolution of the concepts and methods of the calculus of variations in the large, a branch of mathematics that is a little over a century old. The subject of this area is the study of qualitative characteristics of variational problems. In the development
of the calculus of variations in the large several periods can be distinguished with features inherent in each of them. The first period is defined from the end of the 19th century. until the end of the 1940s, when the theory was born and formed, which was formed from two
main parts - the Morse theory and the theory of Lyusternik-Shnirelman categories. Here, the features of traditional mathematics are still noticeable. In the next period - from the end of the 1940s to the end of the 1970s. the calculus of variation in the large was formed as a separate area of mathematics, and it acquired its modern form, based on the concepts and methods of algebraic topology. Ample opportunities opened up for solving new problems in mathematics,
and a number of impressive results were obtained. The modern period can be defined from the late 1970s. until now. Its main feature is the unprecedented convergence of mathematics and the field of its applications, especially with physics. It has not always been possible to
indicate a distinguishable boundary between the two fields of science; even the term "physical mathematics"has appeared. The calculus of variations in the large is included in the qualitative theory, which represents a significant part of modern mathematics and finds wide applications. But its place is even more significant, it is one of the foundations that forms our worldview.

The authors of the article set themselves the task: to familiarize the mathematical community with the history of the citywide algebraic seminar in Tula, which became widely known in the USSR, and then in Russia. The seminar was held at the Tula State Lev Tolstoy Pedagogical
University. Scientists and postgraduates from many cities of the Soviet Union came to Tula to present their research at this seminar (Leningrad, Moscow, Ivanovo, Novosibirsk, Krasnodar, Rostov, etc.). The work of the seminar is associated with the name of M.D.Grindlinger. In the history of the Mathematical Faculty of Tula State Lev Tolstoy Pedagogical University, Doctor of Physical and Mathematical Sciences, Professor Martin Davidovich Grindlinger holds a special place. Many Tula students of M.D. Grindlinger successfully defended their PhD theses: A.E. Ustyan, A.A. Chebotar, V.A. Grinblat, V.N.Bezverkhnii, E.V. Rollov, Yu.A. Ignatov, B.P. Vankov, I.S.Bezverkhnyaya, A.I. Nekritsukhin In 1981, now Professor, Doctor of Physical and Mathematical Sciences N..M. Dobrovolskii enrolled in graduate school to M.D. Grindlinger, who headed the Tula Algebraic School, but nevertheless gave his new graduate student complete creative freedom, thanks to this, N.M. Dobrovolskii classes continued at a seminar with N.M. Korobov at Lomonosov Moscow State University, which played a huge role in the revival of the Tula School of Number Theory. The first of the students of the Tula Algebraic school of M.D.Grindlinger, V.G. Durnev, is a graduate of the faculty, defended his doctoral thesis in 1998, currently he works at Yaroslavl University, V.N. Bezverkhnii, a graduate of the faculty, became the second doctor in 1999. The third doctor was D.I. Moldovanskii (Ivano State University)
I.V. Dobrynina (Moscow), D.N. Azarov and E.V. Sokolov (Ivanovo) defended their doctoral dissertations on the subject of the algebraic scientific school of Grindlinger The work of the algebraic seminar was then headed by the Doctor of Physical and Mathematical Sciences,
Professor Vladimir Nikolaevich Bezverkhnii, a graduate of the faculty - a student of M.D. Grindlinger. This article continues the work of V.G.Durnev and other authors about some teachers who worked at the Faculty of Mathematics of the Tula State Lev Tolstoy Pedagogical
Institute. The main part of the note is the memoirs-reflections of teachers and students of that time period about the formation of an algebraic school in Tula in the last century on the basis of the Tolstoy Tula State Pedagogical Institute and about the role played in this process by the citywide algebraic seminar created by Professor Martin Davidovich Grindlinger. The role of Vladimir Nikolaevich Bezverkhnii is particularly noted. Under their leadership, many Tula students conducted scientific work, who later became candidates and doctors of physical and mathematical sciences. The article presents some of the results obtained by them and their students. This love of science and hard work can serve as an example for modern youth, especially for scientific youth.

The given work is devoted to the study of vortex processes flowing in the liquid spheroidal vortex leading to appearance of fluxes of a substance, which are responsible for appearance of characteristics (potential and intensities) of fields in space surrounding it. In this work we are developing further the proposed by us new physical conception about a vortical state of a substance in the form of a viscous liquid self-closed spheroidal vortex, that allows us to take
a new look at the problems of the existence of different kind of fields of interaction and we elaborate new dynamical theory of emission giving the possibility to have a new look at many processes occurring in Nature. The mechanism of vortex interaction of an emitted matter with the substance in the vortex is also considered.

This year marks the 140th anniversary of the birth of the Polish mathematician Wac law Sierpi´nski, founder of the Warsaw School of Set Theory. The main directions of his research are number theory, set theory, measure theory, topology. Some years spent by him in Moscow, in the atmosphere of a young school of function theory, and collaboration with N.N. Luzin, left an imprint on his further research. Upon returning to his homeland, he managed to captivate and
rally colleagues on the basis of the study and use of set theory, measure theory and topology.
Set theory did not require prior specialization, it united mathematicians of various directions, and its methods made it possible to obtain results at a much lower cost than the methods of special sections of mathematics. Polish journal "Fundamenta Mathematicae"was founded in 1920, was entirely devoted to set theory, had a "Problems"section, and was published in the
main European languages, thanks to which a fruitful international scientific dialogue arose. Numerous studies of Sierpinski himself served as the basis for the studies of his students.

The propagation of acoustic waves in nonlinear elastic anisotropic media with finite preliminary strains is considered. The media in the initial state are homogeneous with an elastic potential in which the first two nonzero terms of expansion in a series by degrees of the strain tensor are preserved. The dynamic equations are written as the equations of propagation of small displacement perturbations imposed on finite strains. The equations are concretized for
the case of propagation of plane monochromatic waves.
An anisotropic material with the symmetry of properties inherent in crystals of cubic symmetry is considered. Constitutive relations of the nonlinear model are written in terms of the basis tensors of the eigen elastic subspaces of the fourth and sixth ranks. The relations include three second-order constants and six third-order constants. A program of experiments for determining the constants of elasticity of a cubic material is proposed.
To determine the elasticity constants of the second order, it is proposed to fulfill an experiment to measure the phase velocities of longitudinal and two transverse waves propagating along the edge of a prismatic sample. To determine the elasticity constants of the third order, the phase velocities of acoustic wave propagation are measured in two samples differing in the orientation of the main axes of anisotropy. In the samples preliminary tension-compression
strains are created along the two edges.
The results of numerical simulation of the proposed experiments for niobium crystals, whose elastic properties are known from sources, are presented. Sections of the surfaces of the phase velocities of longitudinal (quasi-longitudinal) and transverse (quasi-transverse) waves found at different levels of preliminary deformations proposed in the experimental program are constructed. It is shown that not only the values of the wave propagation velocities depend on the level of strains, but also the shape of the cross sections of the phase velocity surfaces with different planes.

This article describes a technique for analyzing the spectra of localized deformation (LD) of products obtained by additive technology (SLM). We used digital-to-analog conversion (DAC) technology. To study the characteristics of periodic (from the place of fixation of the LD on
the estimated length of the sample) and piecewise linear (from the loading time) dependences, a technique for expanding the function of local deformations into a finite Fourier series is described.