С 2012 года в гармоническом анализе на прямой со степенным весом интенсивно изучается двупараметрическое (𝑘, 𝑎)-обобщенное преобразование Фурье, предложенное S. Ben Sa¨ıd, T. Kobayashi, B. Orsted и обобщающее преобразование Данкля (𝑎 = 2), зависящее только от одного параметра 𝑘 ⩾ 0. Вместе с увеличением разнообразия унитарных преобразований наличие параметра 𝑎 > 0 при 𝑎 ̸= 2 приводит к появлению деформационных свойств, например, для функций из пространства Шварца обобщенное преобразование Фурье может не быть бесконечно дифференцируемым или быстро убывающим на бесконечности. Быстрое убывание сохраняется только для последовательности 𝑎 = 2/𝑛, 𝑛 ∈ N. Некоторая замена переменной в этом случае улучшает и другие свойства обобщенного преобразования Фурье. Обобщенное преобразование Данкля, получающееся после замены переменной при 𝑎 = 2/(2𝑟 + 1), 𝑟 ∈ Z+, лишено деформационных свойств и, в значительной степени, уже изучено. В настоящей работе изучается обобщенное преобразование Ганкеля, получающееся после замены переменной при 𝑎 = 1/𝑟, 𝑟 ∈ N. Для него описано инвариантное подпространство из быстро убывающих на бесконечности функций, найден дифференциально-разностный оператор, для которого ядро обобщенного преобразования Ганкеля является собственной функцией. На основе новой теоремы умножения
для функций Бесселя Boubatra — Negzaoui — Sifi построены два оператора обобщенного сдвига, исследована их 𝐿𝑝-ограниченность и положительность. Для теоремы умножения
дано простое доказательство. Определены две свертки, для которых доказаны теоремы Юнга. С помощью сверток определены обобщенные средние, для которых предложены
достаточные условия 𝐿𝑝-сходимости и сходимости почти всюду. Исследованы обобщенные аналоги средних Гаусса — Вейерштрасса, Пуассона и Бохнера–Рисса.

В статье рассматривается задача частичного хеджирования, изучавшаяся в работе [20]. В ней оценивается риск дефицита с использованием выпуклого функционала потерь 𝐿(·).
В нашей работе мы формулируем двойственную задачу, отличную от двойственной задачи в [20], доказываем отсутствие разрыва двойственности, а также существование решения исходной и двойственной задач. Кроме этого, мы получаем результаты статьи [20] при более слабых предположениях, используя подход, связанный с применением теорем выпуклого анализа.

Построен пример пары (2-мерных) 8-вершинных симплициальных тороидальных многогранников (каждый многогранник без самопересечений) с одним и тем же 1-мерным остовом в 3-мерном (евклидовом) пространстве, у которых нет ни одной общей 2-мерной грани, причём объединение 2-мерных остовов этих двух многогранников даёт геометрическую реализацию в 3-мерном пространстве 2-мерного остова 4-мерного гипероктаэдра.
Также построен пример пары 6-вершинных симплициальных многогранных проективных плоскостей с одним и тем же 1-мерным остовом в 4-мерном пространстве, у которых нет
ни одной общей 2-мерной грани, причем объединение этих проективных плоскостей даёт геометрическую реализацию в 4-мерном пространстве 2-мерного остова 5-мерного гипертетраэдра. Наконец, показывается, как можно образно представить атомы в молекуле метана CH4 “связанными” парой внутренне непересекающихся остовных многогранных лент
Мёбиуса.

Рассматривается задача топологической классификации взаимных расположений в вещественной проективной плоскости двух 𝑀-кривых степени 4. На изучаемые расположения наложены условие максимальности (овал одной из этих кривых имеет 16 попарно различных общих точек с овалом другой из них) и условие комбинаторного характера, выделяющее специальный тип таких расположений. Перечислены попарно различные топологические модели расположений этого типа, удовлетворяющие известным фактам о
топологии неособых кривых и топологическим следствиям теоремы Безу. Таких моделей
оказалось 564. Доказано, что 558 моделей не могут быть реализованы кривыми степени
8, остальные 6 моделей удалось построить. Доказательства нереализуемости проводятся
методом Оревкова, основанным на применении теории кос и зацеплений.

Получена асимптотическая формула для количества представлений достаточно большого натурального 𝑁 в виде суммы девяти кубов натуральных чисел 𝑥𝑖, 𝑖 = 1, 9, удовлетворяющих условиям 

$$|(𝑥_𝑖)^3− 𝜇𝑖𝑁| ⩽ 𝐻, 𝜇1 + . . . + 𝜇9 = 1 𝐻 ⩾ 𝑁^)1−(1/30)+𝜀), $$ 

где 𝜇1, . . . , 𝜇9 — положительные фиксированные числа. Этот результат является усилением теоремы Е.М.Райта.

В работе дается обзор по результатам Тульской школы теории чисел по вопросам интерполяции периодических функций многих переменных, заданных в узлах обобщенной параллелепипедальной сетки целочисленной решетки, и по алгоритмам численного инте-
грирования с правилом остановки. Необходимые факты и обозначения приводятся во 2 разделе, который состоит из 6 подразделов: 2.1. Из геометрии чисел; 2.2. Тригонометрические суммы сеток и решёток; 2.3. Неравенства для перенормировок на пространстве (𝐸_𝑠)^a ; 2.4. Интерполяционные формулы для обобщенной параллелепипедальной сетки целочисленной решётки; 2.5. Свойства оператора интерполирования; 2.6. Оценки погрешности
интерполирования. В этих подразделах наряду с известными фактами и определениями,
полученными ранее в Тульской школе теории чисел, содержатся новые понятия и факты
связанные с интерполированием по сдвинутым параллелепипедальным сеткам.
В следующем разделе 3. Алгоритмы приближенного интегрирования и интерполирования с правилом остановки содержится новые определения, связанные с переносом понятия концентрический алгоритм приближенного интегрирования на случай мультипликативного, концентрического алгоритма приближенного интерполирования.
В работе исследуются новые вопросы приближенного интерполирования с правилами
остановки. В 4-ом разделе рассмотрен наиболее важный и интересный для практической
реализации случай вложенных последовательностей параллелепипедальных сеток. Получена оценка нормы разности двух операторов интерполирования по решётке и подрешётке, что позволило в качестве правила остановки концентрического алгоритма приближенного интерполирования периодических функций взять величину максимума модуля разности этих операторов на точках большей параллелепипедальной сетки. В заключении формулируются задача для дальнейшего исследования.

В статье получены проективные инварианты кубических кривых с узловой или изолированной точкой. Доказано, что на проективной плоскости каждые две точки перегиба кубической кривой с узловой (изолированной) точкой находятся в эквиангармоническом
отношении с расположенными на содержащей их прямой точками касательных данной кривой в ее узловой (изолированной) точке. А каждые три точки перегиба такой кривой находятся в квазиангармоническом отношении с расположенной на содержащей их прямой точкой касательной данной кривой в ее узловой (изолированной) точке.
Установлено, что на проективной плоскости любые две крунодальные (акнодальные) кубики проективно эквивалентны.
Доказано, что четыре прямые, содержащие узловую (изолированную) точку кубики, а именно: прямая точек перегиба, касательная и псевдокасательная к кривой в точке перегиба, касательная к кривой в точке, сопряженной с точкой перегиба, находятся в постоянном
сложном отношении, равном −3. На основании этого факта обоснован ряд свойств кубических кривых с узловой (изолированной) точкой на евклидовой плоскости 𝐸2. Приведем некоторые из доказанных свойств, обозначая кубическую кривую символом 𝜎, а ее узловую или изолированную точку — символом 𝐼.
1. Если касательные к 𝜎 в изолированной точке 𝐼 проходят через циклические точки плоскости 𝐸2, то величина угла между любыми двумя прямыми, каждая из которых соединяет точку 𝐼 с точкой перегиба данной кривой, равна 𝜋/3.
2. Псевдокасательная в точке 𝐼 разделяет полосу между проходящими через 𝐼 параллельными касательными к 𝜎 в отношении три к одному, считая от касательной к 𝜎 в сопряженной с 𝐼 точке, тогда и только тогда, когда прямая точек перегиба линии 𝜎 совпадает с абсолютной прямой плоскости 𝐸2.
3. Касательная линии 𝜎 в сопряженной с 𝐼 точке разделяет полосу между взаимно параллельными псевдокасательной в точке 𝐼 и прямой точек перегиба линии 𝜎 в отношении три к одному, считая от псевдокасательной, тогда и только тогда, когда касательная линии 𝜎 в точке 𝐼 совпадает с абсолютной прямой плоскости 𝐸2.
4. Прямая точек перегиба линии 𝜎 разделяет полосу между проходящими через 𝐼 параллельными касательными к 𝜎 в отношении три к одному, считая от касательной линии 𝜎 в точке 𝐼, тогда и только тогда, когда псевдокасательная линии 𝜎 в точке 𝐼 совпадает с абсолютной прямой плоскости 𝐸2.
5. Касательная линии 𝜎 в точке 𝐼 разделяет полосу между прямой точек перегиба и параллельной ей псевдокасательной в точке 𝐼 в отношении три к одному, считая от прямой точек перегиба, тогда и только тогда, когда касательная линии 𝜎 в сопряженной с 𝐼 точке совпадает с абсолютной прямой плоскости 𝐸2.

В работе решено несколько экстремальных задач о наилучшем средне квадратическом приближений функций 𝑓, на полуоси с степенным весом, которые может быть применены при решении различных задач. Получены точные неравенства типа Джексона–Стечкина на некоторых классах функций, в которых величины наилучших приближений оцениваются сверху через модули гладкости Ганкеля 𝑘-го порядка.

В статье исследуются верхние оценки на длины периодов функциональных непрерывных дробей для ключевых элементов гиперэллиптических полей над числовыми полями. В случае, когда гиперэллиптическое поле задается многочленом нечетной степени, конечная длина периода тривиальным образом оценивается сверху удвоенной степенью фундаментальной 𝑆-единицы. Более интересный и сложный случай, когда гиперэллиптическое поле задается многочленом четной степени. В 2019 году В.П. Платоновым и Г.В. Федоровым для гиперэллиптических полей ℒ = Q(𝑥)(√𝑓), deg 𝑓 = 2𝑔 + 2, над полем Q рациональных чисел найден точный промежуток значений 𝑠 ∈ Z таких, что непрерывные дроби элементов вида √𝑓/𝑥𝑠 ∈ ℒ ∖ Q(𝑥) периодические. В данной статье найдено обобщение этого результата для произвольного поля в качестве поля констант. Опираясь на этот результат, найдены точные оценки сверху на длины периодов функциональных непрерывных дробей элементов гиперэллиптических полей над числовыми полями 𝐾, зависящие только от рода 𝑔 гиперэллиптического поля, степени расширения 𝑘 = [𝐾 : Q] и порядка 𝑚 подгруппы кручения якобиана соответствующей гиперэллиптической кривой.

Обнаружение достаточного количества тензорных инвариантов (и не только первых интегралов), как известно [13, 14, 45], позволяет проинтегрировать систему дифференциальных уравнений. Например, наличие инвариантной дифференциальной формы фазового объема позволяет уменьшить количество требуемых первых интегралов. Как известно, для консервативных систем этот факт естественен. Для систем же, обладающих притягивающими или отталкивающими предельными множествами, не только некоторые первые интегралы, но и коэффициенты имеющихся инвариантных дифференциальных форм должны, вообще говоря, включать трансцендентные (т.е. имеющие существенно особые
точки, в смысле комплексного анализа) функции (см. также [1, 23, 24]).
Кратко приведем примеры часто встречающихся тензорных инвариантов. Скалярные инварианты — это первые интегралы рассматриваемой системы. Инвариантные векторные поля — поля симметрий для данной системы (они коммутируют с векторным полем рассматриваемой системы). Фазовые потоки систем дифференциальных уравнений, порождаемых этими полями, переводят решения рассматриваемой системы в решения той
же системы. Инвариантные внешние дифференциальные формы (что, в основном, и проведено в данной работе) порождают интегральные инварианты рассматриваемой системы.
При этом само векторное поле рассматриваемой системы является одним из инвариантов (тривиальный инвариант). Знание тензорных инвариантов рассматриваемой системы дифференциальных уравнений облегчает и ее интегрирование, и качественное исследование. Наш подход состоит в том, что для точного интегрирования автономной системы из 𝑛 дифференциальных уравнений, помимо упомянутого тривиального инварианта, надо знать еще 𝑛 − 1 независимых тензорных инвариантов.
В работе предъявлены тензорные инварианты (дифференциальные формы) для однородных динамических систем на касательных расслоениях к гладким четырехмерным
многообразиям. Показана связь наличия данных инвариантов и полным набором первых интегралов, необходимых для интегрирования геодезических, потенциальных и диссипативных систем. При этом вводимые силовые поля делают рассматриваемые системы диссипативными с диссипацией разного знака и обобщают ранее рассмотренные.

Основной целью этой рукописи является работа над прикладной частью CVMS. В этой работе мы продемонстрировали некоторые общие фиксированные результаты, а затем мы имеем дело в основном с двумя частями приложений, частью (I) комплекснозначной версии существования и общим решением нелинейной краевой задачи второго порядка с использованием функции Грина,

часть (II) Применение результатов с фиксированной точкой для многозначного отображения при настройке виртуальных машин без использования понятия непрерывности. В конце концов, для подтверждения нашего основного результата представлено несколько эквивалентных результатов и примеров.

Пусть 𝑎1, . . . , 𝑎𝑑 – натуральные числа, удовлетворяющие условию 𝑎1 ≥ 𝑎2 ≥ . . . ≥ 𝑎𝑑−1 ≥ 𝑎𝑑 = 1. Определим последовательность {𝑇𝑛} при помощи линейного рекуррентного соотношения 𝑇𝑛 = 𝑎1𝑇𝑛−1 + 𝑎2𝑇𝑛−2 + . . . + 𝑎𝑑𝑇𝑛−𝑑 и начальных условий 𝑇0 = 1,
𝑇𝑛 = 1 + 𝑎1𝑇𝑛−1 + 𝑎2𝑇𝑛−2 + . . . + 𝑎𝑛𝑇0 для 𝑛 < 𝑑. Пусть N(𝑤) – множество натуральных чисел, для которых жадное разложение по линейной рекуррентной последовательности {𝑇𝑛} заканчивается на некоторое слово 𝑤. При этом 𝑤 выбирается так, чтобы множество N(𝑤) было непустым. Рассматривается задача о числе 𝑟𝑘(𝑁) представлений натурального числа 𝑁 в виде суммы 𝑘 слагаемых из N(𝑤).
С использованием полученного ранее описания множеств N(𝑤) в терминах сдвигов торов размерности 𝑑−1 получена асимтотическая формула для числа представлений 𝑟𝑘(𝑁),
а также найдены верхние оценки для числа представлений.
Найдены условия на 𝑘, при выполнении которых искомое представление существует для всех достаточно больших натуральных 𝑁. В частности, такое представление существует, если 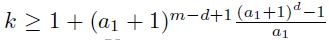, где 𝑚 – длина фиксированного окончания 𝑤 жадного разложения. Кроме того, получена асимтотическая формула для среднего числа представлений.
В заключении сформулировано несколько нерешенных задач.

В работе для разложений действительных чисел по последовательности Фибоначчи доказаны теоремы о равномерном распределении остатков для почти всех чисел в смысле меры Лебега. Вывод этой теоремы основан на критерии Г.Вейля равномерного распределения последовательности по модулю единица и лемме Бореля – Кантелли.

Работа посвящена эволюции понятий и методов вариационного исчисления в целом – раздела математики, возраст которого составляет немного более столетия. Предметом этой области является изучение качественных характеристик вариационных задач. В развитии вариационного исчисления в целом можно выделить несколько периодов с присущими каждому из них чертами. Первый период определим с конца XIX в. до конца 1940-х гг., когда происходит рождение и становление теории, которая сложилась из двух главных частей – теории Морса и теории категорий Люстерника-Шнирельмана. Здесь еще заметно
выступают черты традиционной математики. В следующий период – с конца 1940-х до конца 1970-х гг. вариационное исчисление в целом сформировалась как отдельная область математики, и она обрела свою современную форму, основанную на понятиях и методах алгебраической топологии. Открылись широкие возможности для решения новых задач математики и был получен целый ряд впечатляющих результатов. Современный период
можно определить с конца 1970-х гг. до настоящего времени. Главной его чертой является невиданное ранее сближение математики и области ее приложений, особенно с физикой.
Не всегда стало возможным указать различимую границу между обеими областями науки, появился даже термин «физическая математика». Вариационное исчисление в целом входит в качественную теорию, представляющей значительную часть современной математики и находит широкие применения в приложениях. Но ее место еще более значительно, оно составляет одну из основ, формирующей наше мировоззрение.

Авторы статьи ставили перед собой задачу: ознакомить математическую общественность с историей общегородского алгебраического семинара в Туле, который получил широкую известность в СССР, а потом и в России. Семинар работал в Тульском государственном педагогическом университете им. Л.Н. Толстого. В Тулу приезжали ученые и аспиранты из многих городов Советского Союза, чтобы выступить со своими исследованиями на этом семинаре (Ленинград, Москва, Иваново, Новосибирск, Краснодар, Ростов, и др.). Работа семинара связана с именем М.Д. Гриндлингера. В истории математического факультета ТГПУ им. Л.Н. Толстого доктор физико-математических наук, профессор Гриндлингер Мартин Давидович занимает особое место. Многие тульские ученики М.Д. Гриндлингера успешно защитили кандидатские диссертации: А.Е. Устян, А.А. Чеботарь,
В.А. Гринблат, В.Н. Безверхний, Э.В. Роллов, Ю.А. Игнатов, Б.П. Ваньков, И.С. Безверхняя, А.И. Некрицухин В 1981 году, ныне профессор, доктор физико-математических наук Н.М.Добровольский поступил в аспирантуру к М.Д. Гриндлингеру, который возглавляя Тульскую алгебраическую школу, но тем не менее предоставил своему новому аспиранту полную свободу творчества, благодаря этому продолжились занятия Н.М.Добровольского на семинаре у Н.М. Коробова в МГУ имени М.В. Ломоносова, что сыграло огромную роль в возрождении Тульской школы теории чисел. Первый из учеников Тульской алгебраической школы М.Д. Гриндлингера В.Г. Дурнев -выпускник факультета, защитил докторскую диссертацию в 1998 г, в настоящее время он работает в Ярославском университете, вторым доктором стал в 1999 году В.Н. Безверхний - выпускник факультета. Третьим доктором стал Д.И. Молдованский (Иваноский госуниверситет) По тематике алгебраической науч-
ной школы Гриндлингера защитили докторские диссертации И.В. Добрынина (Москва), Д.Н. Азаров и Е.В. Соколов (Иваново) Работу алгебраического семинара затем возглавил доктор физико-математических наук, профессор Владимир Николаевич Безверхний, выпускник факультета – ученик М.Д. Гриндлингера. Данная статья продолжает работы В.Г. Дурнева и других авторов о некоторых преподавателях, работавших на математическом
факультете Тульского государственного педагогического института имени Л. Н. Толстого. Основная часть заметки – это воспоминания-размышления преподавателей и студентов
того временного периода о формировании в Туле в прошлом веке на базе Тульского государственного педагогического института имени Л.Н. Толстого алгебраической школы и о том, какую роль в этом процессе сыграл созданный профессором Мартином Давидовичем Гриндлингером общегородской алгебраический семинар. Особо отмечается роль Владимира Николаевича Безверхнего. Под их руководством вели научную работу многие тульские студенты, которые впоследствии стали кандидатами и докторами физико-математических наук. В статье приводятся некоторые результаты, полученные ими и их учениками. Эта
любовь к науке и трудолюбие может служить примером для современной молодежи, особенно для научной молодежи.

Данная работа посвящена рассмотрению вихревых процессов, протекающих в жидком сфероидальном вихре, приводящих к появлению потоков вещества, ответственных за появление характеристик (потенциала и напряженности) полей в пространстве, окружающем его. В ней мы развиваем далее выдвинутую нами новую физическую концепцию о вихревом состоянии вещества в виде вязкого жидкого самозамыкающего на себя сфероидального эллиптического вихря, позволяющего по новому взглянуть на проблемы существования различного рода вихревых полей взаимодействия и развиваем новую динамическую теорию отрывных струйных вихревых течений вещества при различной степени возбуждения сфероидального вихря, дающую возможность по новому взглянуть на многие процессы, происходящие в природе. Рассматривается также механизм вихревого взаимодействия испущенного вещества с веществом вихря.

В прошлом году исполнилось 140 лет со дня рождения польского математика Вацлава Серпинского, основателя Варшавской школы теории множеств. Основные направления его исследований теория чисел, теория множеств, теория меры, топология. Несколько лет, проведенных им в Москве, в обстановке молодой школы теории функций, и сотрудничество с Н.Н. Лузиным, наложили отпечаток на его дальнейшие исследования. По возвращении на родину ему удалось увлечь и сплотить коллег на базе изучения и использования теории множеств, теории меры и топологии. Теория множеств не требовала глубокой специализации, объединяла математиков различных направлений, а ее методы позволяли получать результаты с гораздо меньшими затратами, нежели методы специальных разделов математики. Основанный в 1920 г. журнал “Fundamenta Mathematicae” был целиком посвящен теории множеств, имел раздел "Проблемы"и выходил на основных европейских языках, благодаря чему возник плодотворный международный научный диалог. Многочисленные
исследования самого Серпинского послужили основой для исследований его учеников.

Рассматривается распространение акустических волн в нелинейно упругих анизотропных средах с конечными предварительными деформациями. Среды в начальном состоянии однородные с упругим потенциалом, в котором сохраняются два первых ненулевых члена разложения в ряд по степеням тензора деформаций. Динамические уравнения записаны как уравнения распространения малых возмущений перемещений, накладываемых на конечные деформации. Уравнения конкретизированы для случая распространения плоских
монохроматических волн.
Рассмотрен анизотропный материал с симметрией свойств, присущей кристаллам кубической сингонии. Определяющие соотношения нелинейной модели записаны через базисные тензоры собственных упругих подпространств четвертого и шестого рангов. В соотношения входят три константы второго порядка и шесть констант третьего порядка. Предложена программа экспериментов для определения констант упругости кубического материала.
Для определения констант упругости второго порядка предлагается провести эксперимент по измерению фазовых скоростей продольной и двух поперечных волн, распространяющихся вдоль ребра призматического образца. Для определения констант упругости третьего порядка фазовые скорости распространения акустических волн измеряются в двух
образцах, отличающихся ориентацией главных осей анизотропии. В образцах создаются предварительные деформации растяжения-сжатия вдоль двух ребер.
Приведены результаты численного моделирования предложенных экспериментов для кристаллов ниобия, упругие свойства которого известны из источников. Построены сечения поверхностей фазовых скоростей продольных (квазипродольных) и поперечных (квазипоперечных) волн, найденных при различных уровнях предварительных деформаций, предложенных в программе экспериментов. Показано, что от уровня деформаций зависят
не только величины скоростей распространения волн, но и форма сечений поверхностей фазовых скоростей различными плоскостями.

В данной статье описана методика анализа спектров локализованной деформации (ЛД)изделий, полученных по аддитивной технологии (SLM). Использовали технологию цифро-
аналогового преобразования (ЦАП). Для изучения характеристик периодических (от места фиксации ЛД на расчётной длине образца) и кусочно-линейных (от времени нагружения)
зависимостей описана методика разложения функции локальных деформаций в конечный ряд Фурье.