The article is devoted to the 70-th anniversary of Sultan Nazhmudinovich Askhabov, Doctor of Physical and Mathematical Sciences, Professor of the Kadyrov Chechen State University, a well-known specialist in the field of nonlinear integral, integrodifferential, and discrete equations.

A functional system is a set of functions endowed with a set of operations on these functions. The operations allow one to obtain new functions from the existing ones.
Functional systems are mathematical models of real and abstract control systems and thus are one of the main objects of discrete mathematics and mathematical cybernetic.
The problems in the area of functional systems are extensive. One of the main problems is deciding completeness that consists in the description of all subsets of functions that are complete, i.e. generate the whole set.
The well-known Kolmogorov theorem on the representation of continuous functions of several variables in the form of superpositions of continuous functions of one variable and addition adjoins the completeness problem (see the formulation of this theorem below).
The purpose of this paper is the following problem: is there an analogue of Kolmogorov’s theorem on the representation of continuous functions of several variables in the form of superpositions of continuous functions of one variable and addition for functional systems of polynomial functions and functional systems of rational functions?
It turns out that the problem posed (an analogue of Kolmogorov’s theorem) has a negative answer for functional systems of polynomial functions with natural and integer coefficients, and for functional systems of polynomial functions with rational and real coefficients and for functional systems of rational functions with rational and real coefficients - the answer is positive. These theorems are the main results of this paper.

The Sorenson left shift 𝑘-ary gcd algorithm is one of the fastest greatest common divisor algorithms of two natural numbers. At the beginning a natural number 𝑘 > 2 is fixed, which is a parameter of algorithm. At each step we multiply smaller of two input numbers of current step, until it does not become greater of the second number. Then we calculate linear combination
between this number and the bigger of two input numbers. After that we replace the bigger of two input numbers by absolute value of the linear combination. At the end of the algorithm we obtain greatest common divisor of the two original numbers, which has been multiplied by some natural number. Spurious factor has appeared in the answer. We have proven estimation of the worst case of steps and obtained example of this case. Fixation of some endless sequence 𝐾 of natural numbers (each value is greater than 2) allows us to obtain the generalized Sorenson
left shift 𝑘-ary gcd algorithm. There at 𝑖-th step the value of 𝑘𝑖 ∈ 𝐾 is used instead of fixed parameter 𝑘. Both algorithms are completely coincide except this moment.

Continued fractions with rational partial quotients with left shift arise at applying of the generalized Sorenson left shift 𝑘-ary gcd algorithm to the ratio of two natural numbers 𝑎 and 𝑏. We can bind these continued fractions and polynomials of the special form, which called continuants. Numerator and denominator of such continued fractions can be expressed by
continuants. Formulas have been found that allow us to express continuants of the 𝑛-th order as some combination of continuants of a smaller order. Conditions were found at which a sequence of continuants of increasing order is strictly increasing. We also found conditions that allow unambiguous comparison of convergents of rational numbers that had performed by using continued fractions with rational partial quotients.

The generalized Dunkl harmonic analysis on the line, depending on the parameter 𝑟 ∈ N, is studied. The case 𝑟 = 0 corresponds to the usual Dunkl harmonic analysis. All designs depend on the parameter 𝑟 ⩾ 1. Using the generalized shift operator, differences and moduli of smoothness are determined. Using the differential-difference operator, the Sobolev space is defined.We study the approximation of functions from space 𝐿𝑝(R, 𝑑𝜈𝜆) by entire functions of exponential type not higher than 𝜎 from the class 𝑓 ∈ 𝐵𝜎,𝑟
𝑝,𝜆 that have the property 𝑓(2𝑠+1)(0) = 0, 𝑠 = 0, 1, . . . , 𝑟−1. For entire functions from the class 𝑓 ∈ 𝐵𝜎,𝑟
𝑝,𝜆, inequalities are proved that are used in inverse
problems of approximation theory. Depending on the behavior of the values of the function best
approximation, an estimate is given of the modulus of smoothness of the function, as well as the modulus of smoothness on the degree of its second-order differential-difference operator. A condition is given for asymptotic equality between the best approximation of the function and its modulus of smoothness.

When solving the issue of the stability of workings, they often face a situation where destruction occurs only due to the movement of solid blocks, and not their destruction, due to the strength of the rock and rock pressure. In this case, the question arises as to whether the shape of the block (and the worked-out space next to it) is capable of moving under the
influence of gravity or rock pressure into the workings. It is important to take into account the role of friction forces and determine the relative number of dangerous blocks that can fall into the mine. Similar problems arise when studying faults, when protruding blocks can impede movement along the fault. To solve problems related to the kinematics of the block, taking into account these forces, the solutions presented in the works of Goodman and Shi-Gen-Hua were
developed. This article provides a brief overview of the Goodman method with modified proofs of the main theorems, as well as the tasks associated with determining the average number of dangerous blocks. It is assumed that cracks are grouped into a finite number of systems of mutually parallel cracks, which are modeled by planes. Two models are considered - Poisson and equidistant, differing in the distribution of distances between cracks.

To study a block array, it is important to be able to determine the relative number of blocks that satisfy a given property. Thus, when developing a deposit of facing stone, it becomes necessary to determine the distribution of blocks by volume based on data on fracturing. We will assume (unless otherwise stated) that the cracks are modeled by unbounded planes and
are grouped into systems of approximately parallel cracks. Below we consider the model of equidistant cracks and the Poisson model, in which it is assumed that the intersections of each system of cracks with a generic line 𝐿 form a Poisson set of points, and in addition, the unions of any number of these sets of intersection points also form Poisson sets of points. For the model of equally spaced cracks (we will henceforth call it the equally spaced model), an ergodic theorem
is proven that relates the averages over volume and over realizations for the number of blocks satisfying this property. A computer program based on this theorem has been developed. The problems of determining the average volume of a block, the distribution of blocks by volume and the yield of so-called tariff (i.e., having a certain size and shape) blocks when developing a deposit of facing stone using stone-cutting machines are also considered.

An approach to digital controller’s programs design, that perform the functions both sensors and actuators polling control, and control actions calculation, id worked out. Three types of control action computation vector algorithms: the solving systems of difference equations, calculation the digital convolution and PID controller are investigated: It is shown that the
controller, as a real physical device, when implementing a polling program on it, is a timesetting
element, and provides not only a specified peripheral devices polling period, but also time delays between transactions. An estimation of time intervals using the semi-Markov model of the polling algorithm with a Hamiltonian transaction management cycle is made. The model of a closed linear vector control system shows the influence of time delays on such system
characteristics as overshoot and time to reach steady state. A method has been developed for polling algorithm synthesis using a control system matrix model that takes into account the real characteristics of the controller as the device included in the vector feedback loop.

For 𝑛 ≥ 3, an asymptotic formula is derived for the number of representations of a sufficiently
large natural number 𝑁 as a sum of 𝑟 = 2𝑛 + 1 summands, each of which is an 𝑛-th power of
natural numbers 𝑥𝑖, 𝑖 = 1, 𝑟, satisfying the conditions

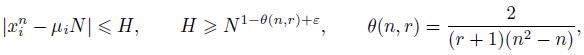
where 𝜇1, . . . , 𝜇𝑟 are positive fixed numbers, and 𝜇1 +. . .+𝜇𝑛 = 1. This result strengthens the theorem of E.M.Wright.

In this paper, we consider the loaded negative order Korteweg–de Vries equation. The evolution of the spectral data of the Sturm–Liouville operator with a potential associated with the solution of the loaded negative order Korteweg–de Vries equation is determined. The obtained results make it possible to apply the inverse problem method to solve the loaded
negative order Korteweg–de Vries equation in the class of rapidly decreasing functions. An example of the given problem is given with graphs of the solution.

This paper provides a generalization of the Hua Loo-Keng estimation method of rational trigonometric sums with a polynomial in exponent in algebraic number fields, which are extensions of the field of rational numbers. In the ring of integers of this algebraic number field we consider integer and fractional ideals. For a complete system of residues for any integer ideal, Hua Loo-Keng proved an analogue of the Euler–Fourier formula, which, using results
regarding the multiplicity of roots of a polynomial congruence modulo a prime ideal (“Hua Loo-Keng trees”), allows the problem to be reduced to the p-adic lifting of solutions, and this allows us to reduce the problem of estimating the sum to estimating the number of solutions of polynomial congruences modulo a power of a prime ideal. Furthermore, building upon Chen Jingrun’s estimates in the field of rational numbers, we obtain improved constants for similar estimates in algebraic numeric fields.

The join of null graph 𝑂𝑚 and complete graph 𝐾𝑛, 𝑂𝑚+𝐾𝑛 = 𝑆(𝑚, 𝑛), is called a complete split graph. In this paper, we characterize chromatically unique, determine list-chromatic number and characterize unique list colorability of the complete split graph 𝐺 = 𝑆(𝑚, 𝑛). We shall prove that 𝐺 is chromatically unique if and only if 1 ⩽ 𝑚 ⩽ 2, 𝑐ℎ(𝐺) = 𝑛 + 1, 𝐺 is uniquely 3-list colorable graph if and only if 𝑚 ⩾ 4, 𝑛 ⩾ 4 and 𝑚+𝑛 ⩾ 10, 𝑚(𝐺) ⩽ 4 for every 1 ⩽ 𝑚 ⩽ 5 and 𝑛 ⩾ 6. Some the property of the graph 𝐺 = 𝑆(𝑚, 𝑛) when it is 𝑘-list colorable graph also proved.

The article proves special cases of the interpolation theorem for the classical predicate calculus without functional symbols and equality. By imposing restrictions on the interpolated formulas, it is possible to prove the existence of an interpolant of a special kind: universal, existential, Horn and universal Horn. The most interesting case is the universal Horn interpolant: the axioms of many algebraic systems are given by universal Horn formulas. The results obtained
in this work can be useful both from the point of view of proof theory and in applications, for example, when solving problems of artificial intelligence and developing logical programming languages. The article is written in the spirit of proof theory, the main tools are sequential calculus and such techniques for proof transforming as reversing the applications of inference
rules, rearranging the applications of rules according to S. K. Kleene and weeding according to V.P.Orevkov.

The article consists of an introduction, the main part divided into 3 paragraphs, and a conclusion. The introduction contains a brief historical overview and discussion of the relevance of the work. In the first paragraph of the main part, the necessary definitions are introduced and the main result is formulated. The second paragraph is devoted to the description of the
sequential calculus KGL constructed by V. P. Orevkov. The third one is devoted to the proof of the main theorem. The conclusion contains a discussion of the results obtained and a brief overview of the prospects for further work.

The article considers the problem of diffraction of a cylindrical sound wave on a homogeneous
isotropic elastic cylinder with a radially inhomogeneous elastic coating located near the
boundary of half-spaces in the case when the linear source is in a plane parallel to the surface of the half-space and is not parallel to the axis of the cylinder. It is assumed that the cylinder is located in a half-space filled with an ideal homogeneous liquid bordering on a homogeneous elastic half-space.
To represent the scattered field in an ideal liquid, a representation in the form of the Helmholtz-Kirchhoff integral is used. The oscillations of an inhomogeneous isotropic elastic body are described by the equations of the linear theory of elasticity. To find the displacement field in an inhomogeneous coating, a boundary value problem for a system of second-order
ordinary differential equations is constructed.
Based on the solution of the direct problem, the inverse problem of determining the laws of coating heterogeneity that provide the least sound reflection in a given frequency range is considered. A functional is constructed expressing the average intensity of sound scattering in a given frequency range. The constructed functional is written in the form of a double integral, which cannot be evaluated analytically. The resulting integral is calculated numerically using a quadrature formula based on a parallelepipedal Korobov grid.
Numerical calculations of the angular characteristics of the scattered field are presented.
A significant effect of continuously inhomogeneous coatings on the diffraction pattern of the scattered field has been revealed.

The article considers the problem of diffraction of a spherical sound wave by an absolutely rigid cylinder with a coating in the form of a homogeneous isotropic elastic layer with an adjacent inhomogeneous liquid layer. It is assumed that a cylinder with a homogeneous coating is surrounded by a continuously inhomogeneous liquid layer with an arbitrary law
of inhomogeneity. A point source of harmonic sound waves is placed in an ideal homogeneous liquid bordering an inhomogeneous layer.
The acoustic pressure in a spherical wave is represented in an integral form as a decomposition in cylindrical wave functions. Wave processes in an elastic layer are described by a system of equations of the linear theory of elasticity of an isotropic body. To determine the wave field in an inhomogeneous liquid layer, a boundary value problem for an ordinary
differential equation of the second order is constructed.

A one-dimensional initial-boundary value problem for a hollow orthotropic multicomponent cylinder under the action of volumetric elastic diffusion perturbations is considered. The mathematical model includes a system of equations of elastic diffusion in a cylindrical coordinate system, which takes into account relaxation diffusion effects, implying finite propagation
velocities of diffusion flows.
The problem is solved by the method of equivalent boundary conditions. To do this, we consider some auxiliary problem, the solution of which can be obtained by expanding into series in terms of eigenfunctions of the elastic diffusion operator. Next, we construct relations that connect the right-hand sides of the boundary conditions of both problems, which are a system of Volterra integral equations of the first kind. A calculation example for a three-component hollow cylinder is considered.

Two models of hypoelastic isotropic materials based on the use of a nonholonomic strain measure, the generalized Yaumann derivative of which coincides with the strain rate tensor, are considered. The conditions under which elastic strain potential exists in such models are formulated. The elastic potential and the constitutive relations are written in terms of elastic
eigen subspaces of an isotropic material. The models differ in the number of elastic constants. It is shown that the four-constant model satisfies the requirements of A.A.Ilyushin particular postulate of isotropy, and the five-constant model does not satisfy them. The equation of acoustic wave propagation in such materials is obtained.

The influence of the use of the particular isotropy postulate as a hypothesis on the results of dynamic problems solution is investigated. The phase velocities of acoustic wave propagation under various types of initial strains are determined for two models. At preliminary purely volumetric strains, calculations using five-constant and four-constant models give the same result. For strains located in the deviatoric subspace, the stress tensor has a component located
in the first elastic eigen subspace, and its projection into the second subspace when using the five-constant model is misaligned to the strain deviator. At the same time, the initially isotropic material acquires anisotropy with respect to acoustic properties. The material model satisfying the particular postulate of isotropy in the case under consideration also describes the anisotropy
of longitudinal waves propagation velocities.

For hypoelastic anisotropic materials, the constitutive relations of nonlinear elasticity are written out. The relations establish a connection between the generalized Yaumann derivatives of the stress tensor and the nonholonomic strain measure introduced in the works of A. A. Markin. The relation is concretized for anisotropic materials with cubic symmetry
of properties. The relations are written in projections into elastic eigen subspaces of a cubic material. The analysis of the mutual influence of finite deformation processes belonging to different eigen subspaces is carried out.

Deformation processes in which the main axes of strains coincide with the same material fibers, whose position relative to the main axes of anisotropy does not change, are considered. Elastic potentials for such processes are written out for two material models: a general one containing nine elastic constants, and a model satisfying the generalization of A. A. Ilyushin
particular postulate to anisotropic materials and containing six constants.

The results of solution of the problem of acoustic wave propagation in hypoelastic anisotropic materials with cubic symmetry of properties are presented. As initial strains of a material, deformations located entirely in its elastic eigen subspaces are considered: purely volumetric
strain, tension-compression in the main axes of anisotropy, pure shear in the plane of the main
axes of anisotropy. Preliminary finite purely volumetric deformations do not affect the shape
of the angular dependences of the phase velocities of wave propagation in the vertical plane, but only affect the values of the phase velocities. At preliminary shaping, the material acquires additional anisotropy, and the shape of the angular dependencies of the phase velocities changes. The results show that in some cases, the six-constant model of the material does not predict a change in the propagation velocities of transverse waves at initial finite strains. 

In the article the problem of the acoustic radiation of a cylinder streamlined by a stationary flow of an ideal liquid is considered It is assumed that the velocity of the incoming flow is significantly lower than the speed of sound. The surface of the spheroid makes harmonic vibrations.
An approximate analytical solution of the problem was obtained with using the speed potential of the oncoming on the body flow and the speed potential of the stationary radiator acoustic field.
Special cases of sound radiation by a cylinder are considered.
The results of numerical calculations of polar diagrams of the acoustic pressure distribution
on the surface of a spheroid at different values of the ratio of the flow velocity to the speed of sound and the wave size of the cylinder are presented.

Within the framework of the nonlinear method of angular boundary functions, the existence of solutions to nonlinear boundary value problems is proven through the construction of barrier functions. Barrier functions are constructed through specially designated support barriers. The support barriers themselves can also act as barrier functions. The resulting inequalities, in turn, are of independent functional interest.

The paper discusses a difference equation of the form
Σ︀𝑟𝑙=0 𝑎𝑘,𝑙𝑍𝑘+𝑙 = 𝑦𝑘 (𝑘 ∈ Z), where 𝑟 ∈ N, 𝑦 = {𝑦𝑘}𝑘∈Z is a given numerical sequence from the space 𝑙𝑝 (1 ⩽ 𝑝 < ∞), provided that the matrix 𝐴 = (𝑎𝑘,𝑙), 𝑎𝑘,𝑙 ∈ R, satisfies some condition close to the presence of a dominant diagonal. With the help of the fixed point theorem, sufficient conditions are written for the
coefficients 𝑎𝑘,𝑙, at which the equation has a unique solution 𝑍 = {𝑍𝑘}𝑘∈Z, belonging to the space 𝑙_𝑝. For the norm of this solution, a numerical estimate is given from above.

In this work, Dirichlet series of 𝑠-dimensional lattices are studied. In particular, the theorem is proved that the Dirichlet series of 𝑠-dimensional lattices are continuous on the space of lattices in the region of their absolute convergence.
In conclusion, current problems for Dirichlet series of 𝑠-dimensional lattices that require further research are considered.

The work constructs a theory of Dirichlet series of the second kind for irreducible lattices repeated by multiplication. In particular, the theorem is proven that Dirichlet series of the second kind for irreducible lattices repeated by multiplication form an algebra over the field of complex numbers.
In conclusion, current problems for Dirichlet series of the second kind for irreducible lattices repeated by multiplication are considered, requiring further research.