Статья посвящена 70-летнему юбилею Асхабова Султана Нажмудиновича, доктора физико-математических наук, профессора Чеченского государственного университета имени А.А. Кадырова, известного специалиста в области нелинейных интегральных, интегро-дифференциальных и дискретных уравнений.

Функциональная система представляет собой множество функций с некоторым набором операций, применяемых к этим функциям и приводящих к получению других функций из этого же множества.
Функциональные системы являются одним из основных объектов дискретной математики и математической кибернетики, поскольку они являются математическими моделями реальных и абстрактных управляющих систем.
Проблематика функциональных систем обширна. Одной из основных задач является проблема полноты, состоящая в описании таких подсистем функций, которые являются полными, т.е. из этих функций с помощью заданных операций над ними можно получить все функции.
К проблеме полноты примыкает известная теорема Колмогорова о представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одной переменной и сложения (формулировку этой теоремы см. ниже).
Целью настоящей статьи является следующая задача: имеет ли место аналог теоремы Колмогорова о представлении непрерывных функций нескольких переменных в виде
суперпозиций непрерывных функций одной переменной и сложения для функциональных
систем полиномиальных функций и функциональных систем рациональных функций ?
Оказывается, что поставленный вопрос (аналог теоремы Колмогорова) имеет отрицательный ответ для функциональных систем полиномиальных функций с натуральными и целыми коэффициентами, а для функциональных систем полиномиальных функций с рациональными и действительными коэффициентами и для функциональных систем рациональных функций с рациональными и действительными коэффициентами – ответ положительный. Эти теоремы и являются основными результатами данной статьи.

Алгоритм Соренсона с левым сдвигом – один из быстрых алгоритмов вычисления наибольшего общего делителя двух натуральных чисел. В начале его работы фиксируется натуральное число 𝑘 > 2, которое является параметром. На каждом шаге алгоритма выполняется поиск линейной комбинации входных чисел текущего шага, причем наименьшее из них предварительно домножается на параметр 𝑘, пока не начнет превосходить наибольшего. После этого наибольшее число замещается абсолютным значением линейной
комбинации. Результатом работы алгоритма является наибольший общий делитель исходных чисел, умноженный на некоторое число, называемое побочным множителем. Для
алгоритма Соренсона была доказана оценка числа шагов в худшем случае, приведен пример. Фиксация некоторой бесконечной последовательности 𝐾 натуральных чисел больших
двух позволяет получить обобщенный алгоритм Соренсона. В нем на каждом шаге вместо числа 𝑘 будет задействовано определенное значение параметра 𝑘𝑖 ∈ 𝐾, соответствующее текущему шагу алгоритма. В остальном алгоритмы полностью совпадают друг с другом.
Цепные дроби с рациональными неполными частными c левым сдвигом возникают в ходе применения к отношению натуральных чисел 𝑎, 𝑏 обобщенного 𝑘-арного алгоритма Соренсона с левым сдвигом. С ними связаны особые формы континуантов, то есть многочленов, при помощи которых выражаются числитель и знаменатель подходящей дроби. Для таких континуантов найдены формулы, позволяющие представить континуант 𝑛-го порядка в виде некоторой комбинации континуантов меньших порядков. Были найдены условия при которых последовательность континуантов увеличивающегося порядка является строго возрастающей. Также были найдены условия, при которых приближения рациональных чисел, выполненные при помощи цепных дробей с рациональными неполными частными, можно однозначно сравнивать.

Изучается обобщенный гармонический анализ Данкля на прямой, зависящий от параметра 𝑟 ∈ N. Случай 𝑟 = 0 ответствует обычному гармоническому анализу Данкля.
Все конструкции зависят от параметра 𝑟 ⩾ 1. С помощью оператора обобщенного сдвига
определяются разности и модули гладкости. С помощью дифференциально-разностного
оператора определяется пространство Соболева. Исследуется приближение функций из пространства 𝐿𝑝(R, 𝑑𝜈𝜆) целыми функциями экспоненциального типа не выше 𝜎 из класса
𝑓 ∈ 𝐵𝜎,𝑟 𝑝,𝜆, обладающих свойством 𝑓(2𝑠+1)(0) = 0, 𝑠 = 0, 1, . . . , 𝑟 − 1. Для целых функций из класса 𝑓 ∈ 𝐵𝜎,𝑟 𝑝,𝜆 доказываются неравенства, которые используются в обратных задачах теории приближений. В зависимости от поведения величин наилучшего приближения функции дается оценка модуля гладкости функции, а так же модуля гладкости от степени ее дифференциально-разностного оператора второго порядка. Дается условие асимптотического равенства между наилучшим приближением функции и ее модулем гладкости.

При решении вопроса об устойчивости выработки часто сталкиваются с ситуацией, когда разрушение происходит только за счет движения цельных блоков, а не их разрушения, из-за прочности породы и горного давления. В таком случае возникает вопрос о том, способна ли форма блока (и выработанного пространства рядом с ним) двигаться под действием силы тяжести или горного давления внутрь выработки. Важно учесть роль сил
трения и определить относительное число опасных блоков, которые могут выпасть в выработку. Аналогичные проблемы возникают при изучении разломов, когда выдвинувшиеся блоки могут препятствовать движению вдоль разлома. Для решения задач, связанных с кинематикой блока при учете указанных сил, были разработаны решения, представленные в работах Гудмана и Ши-Ген-Хуа. В данной статье представлен краткий обзор метода
Гудмана с модифицированными доказательствами основных теорем, а также рассмотрены задачи, связанные с определением среднего числа опасных блоков. Предполагается, что трещины группируются в конечное число систем взаимнопараллельных трещин, которые
моделируются плоскостями. Рассматриваются две модели - пуассоновская и равноотстоящая, отличающиеся распределением расстояний между трещинами.

Для изучения блочного массива важно уметь определять относительное число блоков,
удовлетворяющих данному свойству. Так, при разработке месторождения облицовочного
камня возникает необходимость по данным о трещиноватости определить распределение
блоков по объемам. Будем полагать (если не оговорено противное), что трещины моделируются неограниченными плоскостями и группируются в системы примерно параллельных трещин. Ниже рассматриваются модель равностоящих трещин и пуассоновская модель, в которой предполагается, что пересечения каждой системы трещин с прямой 𝐿 общего положения образуют пуассоновское множество точек, и кроме того, объединения любого числа этих множеств точек пересечения также образуют пуассоновские множества точек.
Для модели равностоящих трещин (мы будем в дальнейшем ее называть равностоящей
моделью ) доказана эргодическая теорема, связывающая средние по объему и по реализациям для чисел блоков, удовлетворяющим данному свойству. Разработана основанная на этой теореме программа для ЭВМ. Также рассмотрены задачи определения среднего объема блока, распределения блоков по объемам и выхода так называемых тарифных (т.е. имеющих определенные размеры и форму) блоков при разработке месторождения облицовочного камня камнерезными машинами.

Разработан подход к конструированию программ цифровых контроллеров, выполняющих функции управления опросом сенсоров и исполнительных устройств, а также расчета векторных управляющих воздействий на объект. Исследованы три типа векторных алгоритмов расчета управляющих воздействий: решение систем разностных уравнений, вычисление цифровой свертки и ПИД регулятор. Показано, что контроллер, как реальный физический прибор, при реализации на нем программы поллинга является времязадающим
элементом, и обеспечивает не только заданный период опроса периферийных устройств,
но и задержки по времени между транзакциями. Произведена оценка временных интервалов по полумарковской модели алгоритма поллинга с гамильтоновым циклом управления транзакциями. На модели замкнутой линейной векторной системы управления показано влияние задержек по времени на такие характеристики системы, как перерегулирование и время выхода на установившийся режим. Разработана методика синтеза алгоритма поллинга по матричной модели системы управления, учитывающей реальные характеристики контроллера как прибора, включаемого в контур векторной обратной связи.

При 𝑛 ⩾ 3 получена асимптотическая формула для количества представлений достаточно большого натурального 𝑁 в виде суммы 𝑟 = 2𝑛 + 1 слагаемых, каждое из которых является 𝑛-ой степенью натуральных чисел 𝑥𝑖, 𝑖 = 1, 𝑟, удовлетворяющих условиям

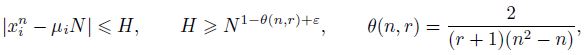где 𝜇1, . . . , 𝜇𝑟 — положительные фиксированные числа и 𝜇1 +. . .+𝜇𝑛 = 1. Этот результат является усилением теоремы Е. М. Райта.

В данной работе мы рассматриваем нагруженное уравнение Кортевега–де Фриза отрицательного порядка. Определена эволюция спектральных данных оператора Штурма–Лиувилля с потенциалом, связанным с решением нагруженного уравнения Кортевега–де Фриза отрицательного порядка. Полученные результаты позволяют применить метод обратной задачи для решения нагруженного уравнения Кортевега–де Фриза отрицательного порядка в классе быстро убывающих функций. Приведен пример иллюстрирующий полученные результаты с графиками.

В настоящей работе дано обобщение метода Хуа Ло-Кена оценки рациональных тригонометрических сумм с многочленом в экспоненте в алгебраических числовых полях,
которые являются расширением поля рациональных чисел. В кольце целых этого алгебраического поля были рассмотрены целые и дробные идеалы. Для полной системы вычетов
по любому целому идеалу Хуа Ло-Кен доказал аналог формулы Эйлера – Фурье, которая позволяет с помощью утверждения о кратности корней полиномиального сравнения по простому идеалу (“деревьев Хуа Лоо-Кена”) свести к задаче p- адического подъема решений. Последнее обстоятельство позволяет привести оценку суммы к получению оценок числа решений полиномиальных сравнений по модулю степени простого идеала. Далее, следуя оценкам Чень Джин-Руна в поле рациональных чисел, в работе найдены более точные константы для подобных оценок в алгебраических числовых полях.

Соединение нулевого графа 𝑂𝑚 и полного графа 𝐾𝑛, 𝑂𝑚 + 𝐾𝑛 = 𝑆(𝑚, 𝑛), называется полным разделенным графом. В этой статье мы характеризуем хроматическую уникальность, определяем хроматический номер списка и характеризуем уникальную раскрашиваемость списка для полного графа разделения 𝐺 = 𝑆(𝑚, 𝑛). Мы докажем, что 𝐺 хроматически уникален тогда и только тогда, когда 1 𝑙𝑒𝑚 𝑙𝑒2, 𝑐ℎ(𝐺) = 𝑛 + 1, 𝐺 является уникальным раскрашиваемым графом с 3-списком тогда и только тогда, когда 𝑚 ⩾ 4,
𝑛 ⩾ 4 и 𝑚 + 𝑛 ⩾ 10, 𝑚(𝐺) ⩽ 4 на каждые 1 ⩽ 𝑚 ⩽ 5 и 𝑛 ⩾ 6. Также доказано некоторое свойство графа 𝐺 = 𝑆(𝑚, 𝑛), когда он представляет собой 𝑘-листовой раскрашиваемый граф.

В статье доказываются специальные случаи интерполяционной теоремы для классического исчисления предикатов без функциональных символов и равенства. Накладывая ограничения на интерполируемые формулы, можно доказать существование интерполянта особого вида: универсального, экзистенциального, хорновского и универсального хорновского. Наиболее интересен случай универсального хорновского интерполянта: аксиомы многих алгебраических систем задаются универсальными хорновскими формулами. Ре-
зультаты, полученные в данной работе, могут быть полезны как с точки зрения теории доказательств, так и в приложениях, например, при решении задач искусственного интеллекта и разработке языков логического программирования. Статья написана в духе теории доказательств, основным инструментом для решения задачи служат секвенциальные исчисления и такие техники преобразования выводов, как обращение применений правил вывода, перестановка применений правил по С. К. Клини и прополка по В. П. Оревкову.
Статья состоит из введения, разбитой на 3 параграфа основной части и заключения.
Введение содержит краткий исторический обзор и обсуждение актуальности работы. В первом параграфе основной части вводятся необходимые определения и формулируется главный результат. Второй параграф посвящён описанию построенного В. П. Оревковым секвенциального исчисления KGL. Третий отведён доказательству основной теоремы. Заключение содержит обсуждение полученных результатов и краткий обзор перспектив дальнейшей работы.

В статье рассматривается задача дифракции цилиндрической звуковой волны на однородном изотропном упругом цилиндре с радиально-неоднородным упругим покрытием, расположенном вблизи границы полупространств в случае, когда линейный источник находится в плоскости, параллельной поверхности полупространства, и не является параллельным оси цилиндра. Полагается, что цилиндр находится в полупространстве, заполненном идеальной однородной жидкостью, граничащем с однородным упругим полупространством.
Для представления рассеянного поля в идеальной жидкости используется представление в виде интеграла Гельмгольца-Кирхгофа. Колебания неоднородного изотропного упругого тела описываются уравнениями линейной теории упругости. Для нахождения поля смещений в неоднородном покрытии построена краевая задача для системы обыкновенных дифференциальных уравнений второго порядка.
На основе решения прямой задачи рассмотрена обратная задача об определении законов неоднородности покрытия, обеспечивающих наименьшее звукоотражение в заданном
частотном диапазоне. Построен функционал, выражающий усредненную интенсивность
рассеяния звука в заданном диапазоне частот. Построенный функционал записывается в
виде двойного интеграла, оценить который аналитически не представляется возможным.
Полученный интеграл рассчитан численно по квадратурной формуле на основе параллепипедальной сетки Коробова.
Представлены численные расчеты угловых характеристик рассеянного поля. Выявлено
существенное влияние непрерывно-неоднородных покрытий на дифракционную картину рассеянного поля.

В статье рассматривается задача дифракции сферической звуковой волны абсолютно жестким цилиндром с покрытием в виде однородного изотропного упругого слоя с прилегающим неоднородным слоем жидкости. Полагается, что цилиндр с однородным покрытием окружен непрерывно-неоднородным слоем жидкости с произвольным законом неоднородности. Точечный источник гармонических звуковых волн помещен в идеальную однородную жидкость, граничащую с неоднородным слоем.
Акустическое давление в сферической волне представляется в интегральной форме в виде разложения по цилиндрическим волновым функциям. Волновые процессы в упругом
слое описываются системой уравнений линейной теории упругости изотропного тела. Для
определения волнового поля в неоднородном слое жидкости построена краевая задача для
обыкновенного дифференциального уравнения второго порядка.

Рассматривается одномерная начально-краевая задача для полого ортотропного многокомпонентного цилиндра, находящегося под действием объемных механодиффузионных
возмущений. Математическая модель включает в себя систему уравнений упругой диффузии в цилиндрической системе координат, в которой учтены релаксационные диффузионные эффекты, подразумевающие конечные скорости распространения диффузионных потоков.
Поставленная задача решается методом эквивалентных граничных условий, согласно
которому рассматривается некоторая вспомогательная задача, решение которой может
быть получено с помощью разложения в ряды по собственным функциям упругодиффузионного оператора. Далее строятся соотношения, связывающие правые части граничных условий обеих задач и представляющие собой систему интегральных уравнений Вольтерры 1-го рода. Рассмотрен расчетный пример для трехкомпонентного полого цилиндра.

Рассматриваются две модели гипоупругих изотропных материалов, основанные на использовании неголономной меры деформаций, обобщенная яуманновская производная от
которой совпадает с тензором деформации скорости. Сформулированы условия, при выполнении которых в таких моделях существует упругий потенциал деформаций. Упругий потенциал и определяющие соотношения выписаны в терминах упругих собственных подпространств изотропного материала. Модели различаются числом упругих констант. Показано, что четырехконстантная модель удовлетворяет требованиям частного постулата изотропии А.А.Ильюшина, а пятиконстантная – не удовлетворяет. Получено уравнение распространения акустических волн в таких материалах.

Исследовано влияние использования частного постулата изотропии в качестве гипотезы на результаты решения динамических задач. Для двух моделей определены фазовые скорости распространения акустических волн при различных видах начальных деформаций. При предварительных чисто объемных деформациях расчеты по пятиконстантной и четырехконстантной моделям дают одинаковый результат. При деформациях, расположенных в девиаторном подпространстве, тензор напряжений имеет составляющую, расположенную в первом упругом собственном подпространстве, а его проекция во второе подпространство при использовании пятиконстантной модели несоосна девиатору деформаций. При этом начально изотропный материал приобретает анизотропию в отношении
акустических свойств. Модель материала, удовлетворяющая частному постулату изотропии, в рассматриваемом случае также описывает анизотропию скоростей распространения
продольных волн.

Для гипоупругих анизотропных материалов выписаны определяющие соотношения нелинейной упругости, устанавливающие связь между обобщенными яуманновскими производными тензора напряжений и неголономной меры деформаций, введенной в работах А.А. Маркина. Связь конкретизирована для анизотропных материалов с кубической симметрией свойств. Соотношения записаны в проекциях в упругие собственные подпространства кубического материала. Проведен анализ взаимного влияния процессов конечного
деформирования, принадлежащих различным собственным подпространствам.

Рассмотрены процессы деформирования, в которых главные оси деформаций совпадают с одними и теми же материальными волокнами, положение которых относительно главных осей анизотропии не изменяется. Для таких процессов выписаны упругие потенциалы для двух моделей материалов: общей, содержащей девять упругих констант, и модели, удовлетворяющей обобщению частного постулата А.А. Ильюшина на анизотропные материалы, содержащей шесть констант.

Приведены результаты решения задачи о распространении акустических волн в гипоупругих анизотропных материалах с кубической симметрией свойств. В качестве начальных деформаций материала рассмотрены деформации, целиком расположенные в его упругих собственных подпространствах: чисто объемная деформация, растяжение-сжатие в главных осях анизотропии, чистый сдвиг в плоскости главных осей анизотропии. Предварительные конечные чисто объемные деформации не оказывают влияния на форму угловых зависимостей фазовых скоростей распространения волн в вертикальной плоскости, а влияют только на величины фазовых скоростей. При предварительном формоизменении материал приобретает дополнительную анизотропию, а форма угловых зависимостей
фазовых скоростей изменяется. Результаты показывают, что в некоторых случаях шестиконстантная модель материала не прогнозирует изменение скоростей распространения поперечных волн при начальных конечных деформациях.

В статье рассматривается задача об акустическом излучении цилиндра, обтекаемого стационарным потоком идеальной жидкости.
Полагается, что скорость набегающего потока значительно меньшей скорости звука.
Поверхность цилиндра совершает гармонические колебания.
Получено приближенное аналитическое решение задачи, построенное с использованием потенциала скорости набегающего на тело потока и потенциала скорости акустического поля неподвижного излучателя.
Рассмотрены частные случаи излучения звука цилиндром.
Представлены результаты численных расчетов диаграмм направленности акустического поля в дальней зоне при разных значениях отношения скорости потока к скорости звука и волнового размера цилиндра.

В рамках нелинейного метода угловых пограничных функций существование решений нелинейных краевых задач доказывается через построение барьерных функций. Барьерные функции конструируются через выделенные специальным образом опорные барьеры. Сами опорные барьеры также могут выступать в роли барьерных функций. Получаемые неравенства в свою очередь представляют самостоятельный функциональный интерес.

В работе рассматривается разностное уравнение вида Σ︀𝑟𝑙=0 𝑎𝑘,𝑙𝑍𝑘+𝑙 = 𝑦𝑘 (𝑘 ∈ Z), где 𝑟 ∈ N, 𝑦 = {𝑦𝑘}𝑘∈Z — заданная числовая последовательность из пространства 𝑙𝑝 (1 ⩽ 𝑝 < ∞), при условии, что матрица 𝐴 = (𝑎𝑘,𝑙), 𝑎𝑘,𝑙 ∈ R, обладает свойством,
близким к наличию доминантной диагонали. С помощью теоремы о неподвижной точке выписаны достаточные условия на коэффициенты 𝑎𝑘,𝑙, при которых данное уравнение имеет единственное решение 𝑍 = {𝑍𝑘}𝑘∈Z, принадлежащее пространству 𝑙𝑝, и для нормы этого решения приведена числовая оценка сверху.

В работе исследуются ряды Дирихле 𝑠-мерных решёток. В частности, доказана теорема, что ряды Дирихле 𝑠-мерных решёток непрерывны на пространстве решёток в области их абсолютной сходимости.
В заключении рассмотрены актуальные задачи для рядов Дирихле 𝑠-мерных решёток, требующие дальнейшего исследования.

В работе построена теория рядов Дирихле второго рода для неприводимых решёток, повторяющихся умножением. В частности, доказана теорема, что ряды Дирихле второго рода для неприводимых решёток, повторяющихся умножением, образуют алгебру над полем комплексных чисел.
В заключении рассмотрены актуальные задачи для рядов Дирихле второго рода для неприводимых решёток, повторяющихся умножением, требующие дальнейшего исследования.