It is known that in mathematical modeling of electromagnetic fields in space, the nature of the electromagnetic process is determined by the properties of the environment. If the medium
is non-conducting, then we obtain multidimensional hyperbolic equations. If the medium has high conductivity, then we come to multidimensional parabolic equations.
Consequently, the analysis of electromagnetic fields in complex media (for example, if the conductivity of the medium changes) is reduced to multidimensional hyperbolic-parabolic equations.
It is also known that vibrations of elastic membranes in space according to Hamilton’s principle can be modeled by multidimensional hyperbolic equations.
The study of the process of heat propagation in a medium filled with mass leads to multidimensional parabolic equations.
Consequently, studying the mathematical modeling of the heat propagation process in vibrating elastic membranes, we also come to multidimensional hyperbolic-parabolic equations.
When studying these applications, it becomes necessary to obtain an explicit representation of
the solutions of the problems under study.
Boundary value problems for hyperbolic-parabolic equations in the plane are well-explored, but their multidimensional analogues have been studied very little. The Tricomi problem for the above equations has been previously investigated on a plane, but far as is known, this problem in space has not been analyzed. In this paper, we show that for the multidimensional model mixed hyperbolic-parabolic equation, the Tricomi problem is non-uniquely solvable. An explicit form of this solution is provided.

In 2001, V.A. Vedernikov and M.M. Sorokina proposed a functional approach to the construction of formations and fitting classes of finite groups by considering, in addition to satellite functions, another type of functions - directions. As a result, 𝜔-fibered (Ω-foliated) formations and Fitting classes of finite groups were constructed, including the well-known 𝜔-
local (Ω-composite) formations and Fitting classes, where 𝜔 is a nonempty set of primes (Ω) — a nonempty subclass of the class of all simple groups). Further research has shown that the concept of foliation can be applied to the construction of foliated formations and Fitting classes of multioperator 𝑇-groups with finite composition series. A new idea in the functional approach of constructing classes of groups was proposed by A.N. Skiba. In a series of articles, he developed the 𝜎-theory of finite groups, where 𝜎 is an arbitrary partition of the set of all primes, and applied its methods to the construction of 𝜎-local formations. Classes generalizing 𝜔-fibered
and Ω-foliated formations and Fitting classes of finite groups were constructed on the basis of the
𝜎-methods. We define classes generalizing the foliated Fitting classes of multioperator T-groups
with composite series and study their minimal and inner satellites.

This paper solves the problem of degree conjugacy of words in a class of sparsely contractible groups.

The question of studying the property of antinormality of subgroups is important, since
this property is used in the study of various properties of groups (for example, hyperbolicity of groups) and various algorithmic problems in groups.
The proposed article gives a complete description of all antinormal two-generated subgroups with a certain condition imposed on the generators of this subgroup contained in a free group of rank greater than one.

In paper, we study uniqueness sets for solutions to the Bessel convolution equation 𝑓𝛼 ⋆𝑔 = 0, 𝛼 ∈ (−1/2,+∞). It is shown, in particular, that if 𝑔 = 𝜒𝑟 is an indicator function of the segment [−𝑟, 𝑟], and an even function 𝑓 ∈ 𝐶(R) satisfies the equation 𝑓𝛼 ⋆𝜒𝑟 = 0
and is zero on (𝑟 − 𝜀, 𝑟) or (𝑟, 𝑟 + 𝜀) for some 𝜀 > 0, then 𝑓 = 0 on (𝑟 − 𝜀, 𝑟 + 𝜀). In this case, the interval
of zeros (𝑟 − 𝜀, 𝑟 + 𝜀), cannot generally be extended. It has been established that a similar phenomenon occurs for solutions of the equation 𝑓𝛼 ⋆𝛿𝑟 = 0, where 𝛿𝑟 is an even measure that maps an even continuous function 𝜙 on R to a number 𝜙(𝑟). Applications of these results to uniqueness theorems for convergent sequences of linear combinations of Bessel functions, the zero set theorem for solutions of the Cauchy problem of the generalized Euler-Poisson-Darboux
equation and the closure theorem of generalized shifts are found.

In a Lebesgue space with weight (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2), where 𝐷 is a finite singly connected domain of the complex plane bounded by a simple closed Lyapunov curve Γ and containing the point 𝑧 = 0, we consider a two-dimensional singular integral operator of the Mikhlin – Calderon – Zygmund type of the form

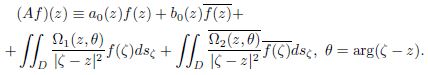
Depending on the homotopy class M𝜈(𝜈 = 0,±1, . . . ,±𝑚) of the operator 𝐴, we establish effective necessary and sufficient conditions for the operator 𝐴 to be Noetherian in (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2) and found formulas for calculating the index of an operator.
The results obtained are applied to the Dirichlet and Neumann problems for general elliptic systems of two equations with two higher-order independent variables.

To solve a problem of preserving a predator-prey biocommunity species structure, a mathematical model of periodic control process is proposed and investigated. A model is based on reducing of continuous dynamics to a discrete one generated by circle homeomorphisms.
The biocommunity dynamics is described by a three dimensional system of ordinary differential equations. Two equations present the Lotka-Volterra system, and the third one describes the dynamics of food attractivity the notion of which was introduced in [1]. The specifics of the system is such that its trajectories belong to cylindrical surfaces. The latter permits to conduct a qualitative research of the system.
The following process is modeled. At some point of time, in order to diminish the growth of prey population, which is considered as a harmful one, a predator population is transferred to a patch. The latter procedure is widely spread in practice while controlling the growth of harmful, invasive, species. If, after a while, the value of food attractivity becomes less than some threshold then the predator population leaves the patch. Thus, there arises a control problem consisting in removal of some part of predator population in such a way that for the remaining part the patch attractivity value becomes more than a threshold.
A notion of admissible piecewise constant control is proposed. The latter takes into account a
possibility of its realization with the less anthropogenic load on a patch. To solve the formulated problem, a method of tangent control is proposed. On the basis of this method, a periodic control process, as the most natural if one takes into account the periodicity of the free Lotka-Volterra
system, is constructed. In this case, a continuous dynamical system is reduced to a discrete one which generates circle homeomorphisms. The conditions under which a dynamical system is periodic are obtained. The explicit expressions for periods are found. The set of attainability is constructed. Also, there is considered a generalization of the control problem consisting in generating of a discrete dynamics which induces double circle rotations. In this case, the problem of finding periodic trajectories is posed.

Groups of form classes were introduced in Number Theory by Gauss, for binary quadratic forms. He defined the notions of equivalence and composition and introduced a group structure in classes of equivalence for the family of quadratic forms with discriminants not divisible by a square of integral number. Further investigations of Gauss were developed in various directions. One of them is a generalization of the theory to multivariate quadratic forms, in which widely studied questions on representation of integral numbers by various quadratic forms. Other direction concerns the notion of composition. But with the growth of the number of variables the question stands very difficult. In 1898, A. Hurwits showed that for quadratic forms with the number of variables greater than 8, it is hard to introduce suitable notion of composition.
This result of A. Hurwits was explaned by Y. V. Linnik from non-associative algebras’ point of a view. It is established that the notion of discriminant for forms of high degree is not so substantive as for quadratic forms. Sometimes, strict difference between forms having one and the same discriminant, is well known. To overcome these difficulties, it is convenient to consider forms connected with given extension of the field.

Many problems in mathematics, mechanics, physics and other engineering disciplines lead to equations in which the unknown function appears under the integral sign. Integral equations are useful mathematical tools in many fields, so they are studied in many different aspects, such as the existence of solutions, approximation of solutions, calculation of correction or incorrigibility, correction of solutions, etc. Many articles mention the so-called PINN (physics-informed neural networks, which can be translated as physically conditioned neural networks), which have found application for solving differential equations, both ordinary and partial derivatives, as
well as systems of differential equations. PINNs are also used to solve integral equations, but publications usually provide methods for solving a certain class of equations, for example, the Fredholm equation of the 2nd kind or the Volterra equation of the 2nd kind. This article will describe a general method for solving continuous integral equations using neural networks that generalizes them to both Fredholm and Volterra integral equations. The essence of the method
is that the desired function is approximated by a neural network, which is essentially a huge function with a large number of adjustable parameters, which are selected from the condition of minimal squared residual, for which the parameters of the neural network are adjusted using the L-BFGS optimization algorithm. The results of the ANN method are compared with the exact solution for several typical integral equations.

Rational approximations on the segment [−1, 1] are studied of singular integrals of the form

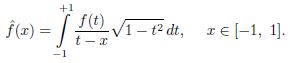
The approximation apparatus is the Abel – Poisson sums of rational integral Fourier operators –
Chebyshev associated with a system of rational Chebyshev – Markov functions, with an arbitrary
fixed number of geometrically different poles. An integral representation of the approximations
is established. In the case when the density of the singular integral has a power-law singularity,
estimates are found pointwise approximations, uniform approximations with a certain majorant,
its asymptotic expression and optimal values of parameters at which the majorant has the highest rate of decrease.
A consequence of the results obtained are estimates of approximations of singular integrals with density having a power-law singularity by Abel – Poisson sums of the polynomial Fourier – Chebyshev series.
Estimates of approximations of singular integrals with a density satisfying the Lipschitz condition on the segment [−1, 1] by Abel – Poisson sums of the polynomial Fourier series – Chebyshev are established. The peculiarity of the estimates found is their dependence on the position of the point on the segment. Moreover, at the ends of the segment, the speed is higher than in the whole segment.
It is established that the classes of studied singular integrals with a density having a powerlaw
singularity in some cases reflect the features of rational approximation in the sense that with a special choice of the velocity parameters of uniform rational approximations they turn out to be higher than the corresponding polynomial analogues.

In the paper we give complete classification of two classes of two-dimensional 𝑃𝐼-algebras over any basic field. The choice of these two classes is predicted by the polynomial identities of the classes: the identity of one of them is given by using the binary operation of the algebra another one involves the bracket operation in the identity. The list of the representatives of isomorphism classes are provided. We compare our list with that obtained earlier, where such a classification was given under certain constraints on the basic field.

In this paper, we study several extreme problems related to the best joint approximation of certain classes of analytical functions in the unit circle given by higher-order continuity modules in the Bergman space 𝐵_2. It should be noted that for the first time the problem of joint approximation of periodic differentiable functions and their consecutive derivatives by trigonometric polynomials and their corresponding derivatives in a uniform metric was
investigated by A.L.Garkavi [1]. The results obtained in [1] were generalized by A.F.Timan [2] for a class of integer functions of exponential type on the entire line. In the monograph [3].
The problems of joint approximation are generalized to some classical theorems of the theory of approximation of functions. However, in the listed works, only asymptotically accurate results were obtained. In this paper, we prove a number of exact theorems for the joint approximation of analytic functions in the unit circle belonging to the Bergman space 𝐵_2, complementing the results of M.Sh.Shabozov [4].

A.O. Gelfond proved that if 𝑏−1 and 𝑑 are coprime, the sums of digits of the 𝑏-ary expressions of natural numbers are uniformly distributed over arithmetic progressions with difference 𝑑. He also obtained a power estimate for the remainder term in this problem.
We consider an analogue of Gelfond’s problem for Zeckendorf representations of naturals as a sum of Fibonacci numbers. It is shown that in this case we again have the uniform distribution of the sums of digits over arithmetic progressions.
Moreover, in the case when the difference of the arithmetic progression 𝑑 is equal to 2, it was previously proved that the remainder term of the problem is logarithmic. In the present paper, it is shown that for 𝑑 ≥ 3 the remainder term of the problem is a power and an unimprovable in order estimate for it is found.
The proof is based on the detailed study of the remainder term at the Fibonacci numbers. It is shown that the remainder term at an arbitrary point can be estimated through the values of the remainder term in points equal to Fibonacci numbers. For them, it is possible to obtain a linear recurrence relation with constant coefficients, and, moreover, and an exact formula in terms of some Vandermonde determinants connected with the roots of the characteristic
polynomial.
Moreover, quite surprisingly, the linear recurrence relation for the remainder term at the Fibonacci points turns out to be connected with some combinatorial triangles, similar to Pascal’s triangle.

The article presents an analysis of solutions to variational problems of mechanics in the works
of Academician O.I. Somov (1815-1876). In 1869 O.I. Somov not only simplifies the solution to Abel’s problem, but also gives a fundamental conclusion about extending the tautochrone problem from the gravity field to any potential field. The article shows how Somov, without using Euler integrals, finds the arc traversed by a body as a function of height, in the case when time does not depend on height (tautochrone). The author of the article examines in detail how, in a kinematic and dynamic problem, Somov immediately abandons Cartesian coordinates,
switching to polar coordinates, saving the reader from endless substitutions.

The article provides brief biographical information about the brilliant, world-famous scientist, academician of the Imperial St. Petersburg Academy of Sciences Pafnutiy Lvovich Chebyshev (1821-1894). The correct emphasis is in the scientist’s surname discussed. The educational, scientific, pedagogical activities and social and administrative work of P.L. Chebyshev are noted. The achievements of P.L. Chebyshev are briefly in the field of mathematics, in more detail - in mechanics presented. Problems of synthesis of mechanisms created by P.L. Chebyshev
are Chebyshev problems called. A generalized Chebyshev problem, which belongs to a new
class of problems in control theory, is considered. The motion program is in the form of an additional system of high-order differential equations formulated. The solution to these problems is on the application of the generalized Gauss principle discussed, which proposed Professor N.N. Polyakhov and his students, S.A. Zegzda, M.P. Yushkov in 1983 at the Department
of Theoretical and Applied Mechanics of Leningrad (St. Petersburg) State University. The influence of the ideas of P.L. Chebyshev is on the content of a two-volume textbook on theoretical and applied mechanics for classical universities discussed. The article reflects the content of the report dedicated to the 300-th anniversary of the Russian Academy of Sciences and St. Petersburg University and heard on February 15, 2024 at a meeting of the section of theoretical mechanics named after Professor N.N. Polyakhov St. Petersburg House of Scientists named after M. Gorky.

In this paper, a variational principle of Lagrange of micropolar theory of elasticity is formulated for a some boundary-value problems. Anisotropic, isotropic and centrally symmetric material are considered. The Ritz method is used to obtain a system of linear algebraic equations in a form of the tensor-block stiffness matrices. The macro-displacement and the micro-rotation are expressed as a sum of products of shape functions and the generalized kinematic nodal fields. For effective approximation of the nearly incompressible micropolar material the generalized
method of reduced and selective integration is used. For testing of described variational model the cylinder torsion problem of the classical and micropolar media is considered. Micropolar continuum exhibit substantial size effects in torsion(and bending)[18]: slender specimens are more rigid than anticipated via classical elasticity. Analytical solution which satisfy integral condition of torsion on the end faces is used.

For a model of a hyperelastic anisotropic material, dynamic equations of acoustic wave propagation, written with respect to the velocity field associated with the passage of the wave are obtained. The propagation of a plane monochromatic wave in a medium with homogeneous preliminary finite strains and initial stresses is considered. It is assumed that during the propagation of sound waves, the gradients of displacements and velocities are small, and the field
of initial stresses is homogeneous. Using these assumptions, the equations of motion, linearized
in the vicinity of the initial stress-strained state are written.
Within the framework of the constructed model, the Christoffel equation, the expression for the radial velocity vector, and the equation of the refraction surface are generalized for the case of a hypoelastic medium. These equations make it possible to analyze the effect of initial stresses on the main characteristics of elastic waves.
The radial velocity vectors describing the energy transfer during the passage of acoustic waves are determined. An expression for the angle that characterizes the deviation of the direction of energy transfer from the direction of wave propagation is obtained. The effect of initial stresses and account of nonlinearity on the deviation of the radial velocity vector from the phase velocity vector compared with the classical solution is considered.
The problem of reflection of a plane elastic wave from a rigid barrier is solved. The influence of initial stresses on the change in the angle of reflection of quasi-longitudinal and quasi-transverse waves from a rigid barrier is considered.
For an anisotropic material with symmetry of properties inherent in cubic crystals, the influence of prestresses on wave propagation characteristics such as phase velocities, directions of polarization vectors, radial velocity vectors and refraction vectors is estimated.

We examine the role that geometrical and topological concepts have played in the recent development of theoretical physics, particularly in the areas of superstring theory and non-Abelian gauge theories. We also demonstrate the importance of these concepts for a better comprehension of the physics’ dynamical laws. In this paper, we present a numerical study of the three-dimensional symmetry breaking dynamics for both non-abelian and abelian Higgs
models. The non-trivial topology of the manifold of vacuum field configurations is the source of the topological excitations in the abelian Higgs model and in the other field theoretic models that
will be discussed. In three-dimensional multicomponent lattice Abelian-Higgs (LAH) models
minimally connected to a noncompact Abelian gauge field, we study the topological phase changes that occur in these models.

The paper investigates the classic problem of covering the start of the natural number series with the minimum number of geometric progressions under various constraints (on the starting point, progression step, and non-intersection of progressions). Among similar problems, the following should be noted: covering arithmetic progressions with geometric progressions with real-valued steps, covering the start of the natural number series with geometric progressions with a fixed number of terms and a real-valued step, and covering the start of the natural
number series with geometric progressions with a rational step. Thus, the uniqueness of the work lies in the constraints imposed on geometric progressions, particularly that the step is a natural number. Optimal solutions were found for cases where: the step constraint is 2, the step constraint is 2 with a prohibition on intersection, and the starting point constraint is 1.
Lower bounds were obtained for cases where: there are no constraints, there is a prohibition on intersection, and there is a step constraint of 3. Upper bounds were obtained for cases where: there are no constraints, and there is a prohibition on intersection.

It has been proved that the dimension of the Lie group of automorphisms of a (2𝑛 + 1)- dimensional smooth manifold endowed with the paracontact metric structure (𝜂, 𝜉, 𝜙, 𝑔) does not exceed (𝑛+1)^2, where 𝜂 is a differential 1-form defining the contact 2𝑛-dimensional distribution 𝐻 = ker𝜂, 𝜉 is a Reeb vector field, 𝜙 is a structural endomorphism, 𝑔 is a pseudo-Riemannian metric whose restriction to the contact distribution 𝐻 has signature (𝑛, 𝑛). The analysis of the conditions for the invariance of the paracontact metric structure with respect to infinitesimal automorphisms, as well as using the Darboux atlas, in each chart of which the contact form
𝜂 has a canonical form, allows us to state that the isotropy group induced by the stationary subgroup of the point 𝑝(0, ..., 0), rotates only vectors lying in the contact plane 𝐻𝑝, and leaves invariant the pseudo-Euclidean metric and the symplectic structure defined by the differential 2-form Ω = 𝑑𝜂. So the maximum dimension of the Lie algebra of the isotropy group is 𝑛^2. Since the dimension of the translation subgroup does not exceed the dimension of the manifold,
the dimension of the automorphism group does not exceed 𝑛2 + 2𝑛 + 1. The paper also proves that the maximum dimension of the Lie algebra of infinitesimal automorphisms is equal to (𝑛 + 1)^2. An example of a paracontact metric manifold admitting a Lie algebra of infinitesimal automorphisms of maximum dimension is the generalized Heisenberg group endowed with a canonical para-Sasakian structure. The basis vector fields of this algebra are found.

This article considers finite groups whose lattice of subgroups satisfy certain generalized semi-modularity conditions. The main result is the theorem: the lattice of subgroups of the finite group 𝐺 is 1-lower semi-modular whenever the lattice of subgroups of 𝐺 is upper semimodular and the lattice of subgroups of any proper subgroup of 𝐺 is lower semi-modular.