Известно, что при математическом моделировании электромагнитных полей в пространстве характер электромагнитного процесса определяется свойствами среды. Если среда непроводящая, то получаем вырождающиеся многомерные гиперболические уравнения. Если же среда обладает большой проводимостью, то приходим к многомерным параболическим уравнениям.
Следовательно, анализ электромагнитных полей в сложных средах (например, если проводимость среды меняется) сводится к многомерным гиперболо-параболическим уравнениям.
Известно также, что колебания упругих мембран в пространстве по принципу Гамильтона можно моделировать вырождающимися многомерными гиперболическими уравнениями.
Изучение процесса распространения тепла в среде, заполненной массой, приводит к
многомерным параболическим уравнениям.
Следовательно, исследуя математическое моделирование процесса распространения
тепла в колеблющихся упругих мембранах, также приходим к многомерным гиперболо-параболическим уравнениям. При изучении этих приложений возникает необходимость получения явного представления решений исследуемых задач. Краевые задачи для гиперболо-параболических уравнений на плоскости хорошо изучены, а их многомерные аналоги исследованы мало. Задача Трикоми для указанных уравнений на плоскости ранее исследована, но насколько нам известно, в пространстве не изучена. В данной работе показано, что для многомерного модельного смешанного гиперболо-параболического уравнения задача Трикоми разрешима неоднозначно. Приводится явный вид этого решения.

В 2001 году В. А. Ведерниковым и М. М. Сорокиной был предложен функциональный подход в построении формаций и классов Фиттинга конечных групп путем рассмотрения помимо функций-спутников еще одного вида функций — направлений. В результате были построены 𝜔-веерные (Ω-расслоенные) формации и классы Фиттинга конечных групп, включающие в себя известные 𝜔-локальные (Ω-композиционные) формации и классы Фиттинга, где 𝜔 — непустое множество простых чисел (Ω — непустой подкласс класса всех простых групп). Дальнейшие исследования показали, что понятие расслоенности может быть применено к построению расслоенных формаций и классов Фиттинга мультиоператорных 𝑇-групп с конечными композиционными рядами. Новая идея в функциональном подходе построения классов групп была предложена А. Н. Скибой. В серии статей он разработал 𝜎-теорию конечных групп, где 𝜎 — произвольное разбиение множества всех простых чисел, и применил ее методы к построению 𝜎-локальных формаций. На основе 𝜎-методов были построены классы, обобщающие 𝜔-веерные и Ω-расслоенные формации и классы Фиттинга конечных групп. В настоящей работе определены классы, обобщающие расслоенные
классы Фиттинга мультиоператорных 𝑇-групп, обладающих композиционными рядами, изучены их минимальные и внутренние спутники.

В статье решена проблема степенной сопряженности слов в классе малосократимых групп.

Вопрос об изучении свойства антинормальности подгрупп является важным, так как это свойство используется при изучении различных свойств групп (например, гиперболичности групп) и различных алгоритмических проблем в группах.
В предлагаемой статье дано полное описание всех антинормальных двупорожденных подгрупп со определенным условием, налагаемым на образующие данной подгруппы, содержащиеся в свободной группе ранга больше единицы.

В статье изучаются множества единственности для решений уравнения свертки Бесселя 𝑓𝛼 ⋆𝑔 = 0, 𝛼 ∈ (−1/2,+∞). Показано, в частности, что если 𝑔 = 𝜒𝑟 – индикатор отрезка [−𝑟, 𝑟], а чётная функция 𝑓 ∈ 𝐶(R) удовлетворяет уравнению 𝑓𝛼 ⋆ 𝜒𝑟 = 0 и равна нулю на (𝑟 − 𝜀, 𝑟) или (𝑟, 𝑟 + 𝜀) при некотором 𝜀 > 0, то 𝑓 = 0 на (𝑟 − 𝜀, 𝑟 + 𝜀). При этом интервал нулей (𝑟 − 𝜀, 𝑟 + 𝜀), вообще говоря, расширить нельзя. Установлено, что подобное явление имеет место и для решений уравнения 𝑓 𝛼 ⋆ 𝛿𝑟 = 0, где 𝛿𝑟 – чётная мера, сопоставляющая чётной непрерывной функции 𝜙 на R число 𝜙(𝑟). Найдены приложения этих результатов к теоремам единственности для сходящихся последовательностей линейных комбинаций
функций Бесселя, теоремам о нулевых множествах для решений задачи Коши обобщенного уравнения Эйлера-Пуассона-Дарбу и теоремам о замыкании обобщенных сдвигов.

В лебеговом пространстве с весом (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2), где 𝐷 – конечная
односвязанная область комплексной плоскости, ограниченная простой замкнутой кривой
Ляпунова Γ, и содержащая внутри точку 𝑧 = 0, рассматривается двумерный сингулярный
интегральный оператор типа Михлина – Кальдерона – Зигмунда вида

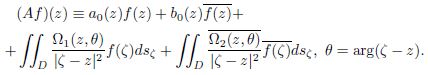
В зависимости от гомотопического класса M𝜈(𝜈 = 0,±1, . . . ,±𝑚) оператора 𝐴 установлены эффективные необходимые и достаточные условия нётеровости оператора 𝐴 в (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2) и найдены формулы для подсчёта индекса оператора.
Полученные результаты применяются к задачам Дирихле и Неймана для общих эллиптических систем двух уравнений с двумя независимыми переменными высшего порядка.

Предлагается и исследуется математическая модель периодического процесса управления, предназначенная для решения экологической проблемы сохранения видовой структуры биосообщества «хищник-жертва».Модель основана на сведении непрерывной динамики
к дискретной, порожденной гомеоморфизмами окружности.
Динамика взаимодействия видов описывается трехмерной системой обыкновенных
дифференциальных уравнений. Два уравнения задают систему Лотки – Вольтерры, а третье — динамику пищевой привлекательности участка, понятие которой введено в [1]. Специфика системы такова, что ее траектории принадлежат инвариантным цилиндрическим поверхностям, что позволяет провести полное качественное исследование системы.
Моделируется следующий процесс. В некоторый момент времени на участок вводится популяция хищника для уменьшения роста популяции жертвы, которая рассматривается как вредный вид. Это широко распространенная в практике процедура борьбы с вредными инвазивными видами. Если через некоторое время значение пищевой привлекательности участка становится меньше порогового значения, то популяция хищника покидает участок.
Ставится задача управления, состоящая в изъятии части популяции хищника так, чтобы для оставшейся части значение пищевой привлекательности было больше порога.
Вводится понятие допустимого кусочно постоянного управления, которое учитывает
возможность его практической реализации при наименьшей антропогенной нагрузке на
участок. Для решения поставленной задачи предлагается метод касательных управлений,
на основе которого построен периодический процесс управления, как наиболее естествен-
ный, если учесть периодичность свободной системы Лотки – Вольтерры.
При построении периодического процесса управления непрерывная динамика сводится
к дискретной, которая порождает гомеоморфизмы окружности. Получены условия, при которых система периодична. Найдены явные выражения для периодов. Построено множество управляемости. Рассмотрено обобщение задачи, при котором непрерывная динамика индуцирует дискретную, порождающую двойные повороты окружности. Ставится задача нахождения периодических траекторий.

В теории чисел группы классов форм были введены Гауссом для бинарных квадратичных форм. Гаусс ввел понятия эквивалентности и композиции и определил групповую структуру во множестве классов эквивалентности в семействе квадратичных форм с дискриминантами, не делящимися на квадрат целого числа. Дальнейшие исследования были развиты в разных направлениях. Одним из них является обобщение теории на квадратичные формы от большего числа переменных, где широко изучены вопросы, связанные с представлением целых чисел различными квадратичными формами. Другое направление относится к понятию композиции. Однако с ростом количества переменных становится все труднее введение понятия композиции форм. В 1898 г. А. Гурвиц показал, что для квадратичных форм с числом переменных больше 8 очень сложно ввести удовлетворительное понятие композиции. Этот феномен впоследствии был разъяснен Ю. В. Линником с точки зрения теории некоммутативных алгебр с делением. Установлено, что понятие «дискриминанта» не имеет столь существенного значения для форм высших степеней, чем для
квадратичных форм. Хорошо известна строгая разница между свойствами форм степени
выше 2 с одинаковыми дискриминантами. Для устранения этих трудностей удобно рассмотреть формы, связанные с данным расширением.

Многие задачи математики, механики, физики и других инженерных дисциплин приводят к уравнениям, в которых неизвестная функция стоит под знаком интеграла. Интегральные уравнения являются полезными математическими инструментами во многих областях, поэтому они исследуются во многих различных аспектах, таких, как существование решений, аппроксимация решений, расчет поправки или неисправимости, корректировка решений и т. д. Во многих статьях упоминаются так называемые PINN (physicsinformed neural networks, что можно перевести как физически обусловленные нейронные сети), которые нашли применение для решения дифференциальных уравнений, как обыкновенных, так и в частных производных, а также систем дифференциальных уравнений.
PINN также применяются для решения интегральных уравнений, однако, в публикациях
обычно приводятся методы для решения некоторого класса уравнений, к примеру, уравнения Фредгольма 2-го рода либо уравнения Вольтерра 2-го рода. В этой статье будет описан общий метод решения непрерывных интегральных уравнений с помощью нейросетей, который обобщает их как для интегральных уравнений Фредгольма, так и для интегральных уравнений Вольтерра. Суть метода заключается в том, что искомая функция аппроксимируется нейронной сетью, которая по сути является огромной функцией с большим числом настраиваемых параметров, которые выбираются из условия минимальности квадрата невязки, для чего параметры нейронной сети настраиваются с помощью алгоритма оптимизации L-BFGS. Результаты метода ANN сравниваются с точным решением для нескольких типовых интегральных уравнений.

Изучаются рациональные аппроксимации на отрезке [−1, 1] сингулярных интегралов вида

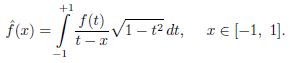Аппаратом приближений являются суммы Абеля – Пуассона рациональных интегральных операторов Фурье – Чебышёва, ассоциированные с системой рациональных функций Чебышёва – Маркова, с произвольным фиксированным количеством геометрически-различных полюсов. Установлено интегральное представление приближений. В случае, когда плотность сингулярного интеграла имеет степенную особенность, найдены оценки поточечных приближений, равномерных приближений с определенной мажорантой, ее асимптотическое выражение и оптимальные значения параметров, при которых мажоранта имеет наибольшую скорость убывания.
Следствием полученных результатов являются оценки приближений сингулярных интегралов с плотностью, имеющей степенную особенность, суммами Абеля – Пуассона полиномиального ряда Фурье – Чебышёва.
Получены оценки приближений сингулярных интегралов с плотностью, удовлетворяющей на отрезке [−1, 1] условию Липшица, суммами Абеля – Пуассона полиномиального ряда Фурье – Чебышёва. Особенностью найденных оценок является их зависимость от положения точки на отрезке. Причем на концах отрезка скорость является выше, чем в целом на отрезке.
Установлено, что классы изучаемых сингулярных интегралов с плотностью, имеющей степенную особенность, в некоторых случаях отражают особенности рациональной аппроксимации в том смысле, что при специальном выборе параметров скорости равномерных рациональных приближений оказываются выше соответствующих полиномиальных аналогов.

В статье дана полная классификация двух классов двумерных 𝑃𝐼-алгебр над любым основным полем. Выбор этих двух классов обусловлен полиномиальными тождествами классов: тождество одного из них дается с помощью бинарной операции алгебры, а другого - с помощью скобочной операции в тождестве. Приведен список представителей классов
изоморфизма. Мы сравниваем наш список со списком, полученным ранее, где подобная
классификация была дана при определенных ограничениях на основное поле.

В работе изучается ряд экстремальных задач, связанных с наилучшим совместным приближением некоторых классов аналитических в единичном круге функций, задаваемых модулями непрерывности высших порядков в пространстве Бергмана 𝐵_2. Отметим, что впервые задача совместного приближения периодических дифференцируемых функций и их последовательных производных тригонометрическими полиномами и их соответствующими производными в равномерной метрике была исследована А.Л.Гаркави [1].
Полученные в [1] результаты были обобщены А.Ф.Тиманом [2] на классе целых функций
экспоненциального типа на всей прямой. В монографии [3] задачи совместного приближения обобщены на некоторых классических теоремах теории аппроксимации функций.
Однако в перечисленных работах получены только асимптотически точные результаты.
В данной работе доказан ряд точных теорем совместного приближения аналитических
в единичном круге функций, принадлежащих пространству Бергмана 𝐵_2, дополняющих
результаты М.Ш. Шабозова [4].

А. О. Гельфонд доказал, что при условии взаимной простоты 𝑏 − 1 и 𝑑 суммы цифр разложений натуральных чисел в 𝑏-ичную систему счисления равномерно распределены по арифметическим прогрессиям с разностью 𝑑. Также он получил степенную оценку остаточного члена в данной задаче.
Мы рассматриваем аналог задачи Гельфонда для представлений Цекендорфа натуральных чисел в виде суммы чисел Фибоначчи. Показано, что в данном случае также имеет место равномерная распределенность сумм цифр по арифметическим прогрессиям. Более того, в случае, когда разность арифметической прогрессии 𝑑 равняется 2, ранее было доказано, что остаточный член задачи является логарифмическим. В настоящей работе
показано, что при 𝑑 ≥ 3 остаточный член задачи является степенным и найдена неулучшаемая по порядку оценка для него.
В основе доказательства лежит детальное изучение остаточного члена в точках, равных числам Фибоначчи. Показано, что остаточный член в произвольной точке может быть оценен через значения остаточного члена в числах Фибоначчи. Для последних удается получить линейное рекуррентное соотношение с постоянными коэффициентами, и, более того, точную формулу в терминах некоторых определителей Вандермонда, связанных с корнями характеристического многочлена.
Кроме того, достаточно неожиданно линейное рекуррентное соотношение для остаточного члена в точках, равных числам Фибоначчи, оказывается связанным с некоторыми комбинаторными треугольниками, аналогичными треугольнику Паскаля.

В статье представлен анализ решений вариационных задач механики в работах академика О. И. Сомова (1815-1876). В 1869 году О. И. Сомов не только упрощает решение задачи Абеля, но и приводит фундаментальный вывод о расширении задачи таутохроны с поля силы тяжести на любое потенциальное поле. В статье показано, как Сомов, не используя интегралы Эйлера, находит дугу, пройденную телом в функции высоты, в том случае, когда время не зависит от высоты (таутохрона). Автор статьи подробно рассматривает, каким образом в кинематической и динамической задаче Сомов сразу же отказывается от декартовых координат, переходя на полярные координаты, избавляя читателя от бесконечных замен.

В статье приводятся краткие биографические сведения о гениальном, всемирно известном учёном, академике Императорской Санкт-Петербургской академии наук Пафнутии Львовиче Чебышёве (1821-1894). Обсуждается правильное ударении в фамилии учёного. Отмечаются учебно-научная, педагогическая деятельность и общественно-административная работа П.Л. Чебышёва. Сжато излагаются достижения П. Л. Чебышёва в области математики, более подробно – в механике. Задачи синтеза механизмов, созданных П. Л. Чебышёвым, называются задачами Чебышёва. Формулируется обобщённая задача Чебышёва, относящаяся к новому классу задач теории управления, в котором программа движения задаётся в виде дополнительной системы дифференциальных уравнений высокого
порядка. Обсуждается решение этих задач на основе применения обобщённого принципа
Гаусса, предложенное профессором Н. Н. Поляховым и его учениками, С. А. Зегждой,
М. П. Юшковым в 1983 году на кафедре теоретической и прикладной механики Ленин-
градского (Санкт-Петербургского) государственного университета. Обсуждается влияние идей П.Л. Чебышёва на содержание двухтомного учебника по теоретической и прикладной механике для классических университетов. Статья отражает содержание доклада, приуроченного к 300-летию РАН и Санкт-Петербургского университета и заслушанного
15 февраля 2024 года на заседании секции теоретической механики имени профессора
Н.Н. Поляхова Санкт-Петербургского Дома учёных имени М. Горького.

Для решения некоторых краевых задач микрополярной теории упругости в работе формулируется вариационный принцип Лагранжа в обобщённых кинематических полях применительно к материалам с центром симметрии произвольной анизотропии
[5, 6, 7, 8, 9, 10, 11]. Используя метод Ритца краевая задача приводится к тензорно-блочной системе линейных алгебраических уравнений. Для чего искомые кинематические векторные поля перемещений и микровращений раскладываются в ряд по базисным кусочно-полиномиальными функциям лагранжева(8-узлового КЭ) и серендипова (20-узлового КЭ) семейства[8, 14]. Для улучшения аппроксимации лагранжевыми многочленами(8-узлового КЭ), в том числе для почти несжимаемой среды, использован обобщенный метод редуцированного и селективного интегрирования[11]. Апробация построенной математической модели выполняется на задаче о кручении изотропного цилиндрического тела в рамках классической и микрополярной теории упругости с демонстрацией масштабного эффекта,
в том числе по результатам экспериментальных данных [18]. Представлено сравнение полученного численного решения с аналитическим решением Сен-Венана[3] симметричной теории упругости; с аналитическим решением Готье, Ясмана[15, 16] и численным решением авторов [7] для микрополярной среды; с результатами эксперимента Лейкса[18]. При задании интегральных граничных условий(момента) на торцевой поверхности цилиндрического тела было использовано аналитическое распределение касательных и моментных напряжений [3, 15, 16].

Для модели гипоупругого анизотропного материала получены динамические уравнения
распространения акустических волн, записанные относительно поля скоростей, связанного с прохождением волны. Рассматривается распространение плоской монохроматической
волны в среде с однородными предварительными конечными деформациями и начальными напряжениями. Предполагается, что при распространении звуковых волн градиенты
перемещений и скоростей малы, а поле начальных напряжений однородно. С использованием этих допущений записаны уравнения движения, линеаризованные в окрестности начального напряженно-деформированного состояния.
В рамках построенной модели получены обобщенные на случай гипоупругой среды
уравнение Кристоффеля, выражение для вектора лучевой скорости, уравнение поверхности рефракции. Эти уравнения позволяют проанализировать влияние начальных напряжений на основные характеристики упругих волн.
Определены векторы лучевых скоростей, описывающие перенос энергии при прохождении акустических волн. Найдено выражение для угла, который характеризует отклонение направления переноса энергии от направления распространения волны. Рассмотрено влияние начальных напряжений и учета нелинейности на отклонение вектора лучевой скорости от вектора фазовой скорости по сравнению с классическим решением.
Решена задача об отражении плоской упругой волны от жесткой преграды. Рассмотрено влияние начальных напряжений на изменение угла отражения квазипродольных и квазипоперечных волн от жесткой преграды.
На примере анизотропного материала с симметрией свойств, присущих кубическим
кристаллам, проведена оценка влияния предварительных напряжений на такие характеристики распространения волн, как фазовые скорости, направления векторов поляризации, векторы лучевых скоростей и векторы рефракции.

Мы рассматриваем роль, которую геометрические и топологические концепции сыграли в недавнем развитии теоретической физики, особенно в области теории суперструн и неабелевых калибровочных теорий. Мы также демонстрируем важность этих концепций для лучшего понимания динамических законов физики. В данной работе мы представляем численное исследование динамики трехмерного нарушения симметрии для неабелевых и абелевых моделей Хиггса. Нетривиальная топология многообразия конфигураций вакуумного поля является источником топологических возбуждений в абелевой модели Хиггса и в других теоретико-полевых моделях, которые будут обсуждаться далее. В трехмерных многокомпонентных решетчатых абелево-хиггсовских (LAH) моделях, минимально связанных с некомпактным абелевым калибровочным полем, мы изучаем топологические фазовые изменения, происходящие в этих моделях.

В работе исследуется классическая задача о минимальном накрытии начала натурального ряда минимальным числом геометрических прогрессий с рядом некоторых ограничений(на начало прогрессии, на шаг прогрессии и на непересечение прогрессий). Среди схожих к ней задач следует отметить следующие задачи: о накрытии арифметических прогрессий геометрическими с действительнозначным шагом, о накрытии начала натурального ряда геометрическими прогрессиями с фиксированным числом членов, где шаг действительнозначен и о накрытии начала натурального ряда геометрическими прогрессиями с рациональным шагом. Таким образом, уникальность работы заключается в наличии ограничений на геометрические прогрессии и тем, что шаг является натуральным числом.
Найдены оптимальные ответы для случаев, когда: ограничение на шаг равно 2, ограничение на шаг равно 2 и имеется запрет на пересечение, ограничение на начало равно 1. Были получены оценки снизу для случаев, когда: нет ограничений, есть ограничение на непересечение, есть ограничение на шаг равное 3. Были получены оценки сверху для случаев когда: нет ограничений, есть ограничение на непересечение.

Доказано, что размерность группы Ли автоморфизмов (2𝑛 + 1)-мерного гладкого многообразия, наделённого параконтактной метрической структурой (𝜂, 𝜉, 𝜙, 𝑔), не превосходит (𝑛 + 1)2, где 𝜂 – дифференциальная 1-форма, определяющая контактное 2𝑛-мерное
распределение 𝐻 = ker𝜂, 𝜉 – векторное поле Риба, 𝜙 – структурный эндоморфизм, 𝑔 – псевдориманова метрика, ограничение которой на контактное распределение 𝐻 имеет сигнатуру (𝑛, 𝑛). Анализ условий инвариантности параконтактной метрической структуры относительно инфинитезимальных автоморфизмов, а также используя атлас Дарбу, в каждой карте которого контактная форма 𝜂 имеет канонический вид, позволяет утверждать, что группа изотропий, индуцированная стационарной подгруппой точки 𝑝(0, ..., 0), вращает только векторы, лежащие в контактной плоскости 𝐻𝑝, и оставляет инвариантной псевдоевклидову метрику и симплектическую структуру, определяемую дифференциальной 2-формой Ω = 𝑑𝜂. Поэтому максимальная размерность алгебры Ли группы изотропий равна 𝑛2. Так как размерность подгруппы сдвигов не превосходит размерность многообразия, то размерность группы автоморфизмов не превосходит 𝑛2 + 2𝑛 + 1. В данной работе также доказано, что максимальная размерность алгебры Ли инфинитезимальных
автоморфизмов равна (𝑛 + 1)^2. Примером параконтактного метрического многообразия,
допускающего алгебру Ли инфинитезимальных автоморфизмов максимальной размерности, является обобщённая группа Гейзенберга, наделённая канонической парасасакиевой
структурой. Найдены базисные векторные поля этой алгебры.

В данной работе рассматриваются конечные группы, решётки подгрупп которых удовлетворяют некоторым условиям обобщённой полумодулярности. Основным результатом
является теорема: если решётка подгрупп конечной группы 𝐺 является верхне полумодулярной, а решётка подгрупп любой её собственной подгруппы является нижне полумодулярной, то решётка подгрупп группы 𝐺 является 1-нижне полумодулярной.