Billiards in three-dimensional confocal domains with slipping along the boundary are considered. Such dynamical systems are Liouville integrable in piecewise-smooth sense. In twodimensional case, class of billiards with slipping was introduced by A.T.Fomenko. For several types of confocal billiards with slipping the classes of homeomorphism of constant energy surfaces are found, the bifurcation diagrams are constructed and the topology of Liouville foliation in small neighborhoods of singular and non-singular fibers is described.

Bipartite immersions of a bipartite graph into a plane with a minimum self-intersection number are studied. For some classes of bipartite graphs, the minimum self-intersection number is calculated for all bipartite immersions. In particular, all graphs with a bipartite embedding
into a plane are described. Appendixes are given to the chronological ordering of the initial coinage of Shirvanshah Abu Mansur Ali bin Yazid (425-435 AH = 1034-1044 AD).

This work is devoted to the study of geodesics in the class of metric spaces endowed with the Gromov–Hausdorff distance. The study shows that the construction of a linear geodesic is impossible in the general case, even if we consider the Gromov – Hausdorff class factored by zero
distances. Moreover, it is established that the optimal Hausdorff realization divides metric spaces at zero distance into equivalence classes with matching completions. It is also demonstrated how
to construct a geodesic in Hansen’s example using 0-modifications. Nevertheless, it is shown that, in general, it is impossible to construct a geodesic using the optimal Hausdorff realization.
This shows that geodesics in the class of metric spaces have an even richer structure, and the methods for constructing geodesics from the Gromov – Hausdorff space cannot be transferred to the class of metric spaces.

In this paper theorems on the representations of real numbers 𝛼 by using infinite iteration of a sequence of positive monotonic functions 𝛼𝑛 = 𝑓_𝑛(𝑥_𝑛) in the form

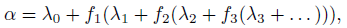
where “digits” 𝜆_𝑛, 𝑛 ≥ 0, and “remainders”

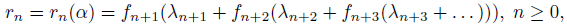
are defined by the following recurrent formulas

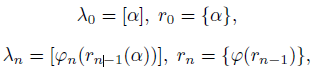
moreover {𝑧} and [𝑧] denote accordingly the fractional and the integral parts of the real number 𝑧, and 𝑥𝑛 = 𝜙𝑛(𝛼𝑛), 𝑛 ≥ 1, are inverse functions of 𝛼𝑛 = 𝑓𝑛(𝑥𝑛).

In particular, the representation of the number 𝛼 by using function 𝑓(𝑥) = 1/𝑥 leads to the continued fraction of the number 𝛼. The general case when 𝑓(𝑥) is decreasing function have been considered by B.H. Bissinger (1944) and A. R´enyi (1957). For the function 𝑓(𝑥) = 𝑥
𝑞 as 𝑞 ≥ 2 is the natural number, is obtained 𝑞-adic the representation of the form 𝛼 = Σ︀ 𝜆𝑛𝑞−𝑛, where digits 𝜆𝑛, 𝑛 ≥ 1, can to receive all integral values from 0 to 𝑞 − 1. The case when 𝑓(𝑥) is increasing
function have been investigated by C.I. Everett (1946) and A. R´enyi (1957). The representation 𝛼 for 𝑓(𝑥) = 𝑥 𝜃 is nonintegral number 𝜃 > 1 have been studied A. R´enyi (1957) and A.O. Gelfond (1959). In the present paper for the sequence of functions 𝑓𝑛(𝑥) = 𝑥 𝑞𝑛 , 𝑞𝑛 ≥ 2, are
integer, has been investigated the representation of 𝛼 on the multiplicative system of numbers as 𝑛 ≥ 1 in the form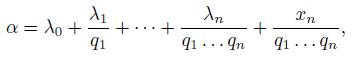

where digits 𝜆𝑛 can to receive integral values from 0 to 𝑞𝑛 − 1.

A. Kh. Ghyasi (2007) has been generalized Gelfond theorem concerning the multiplicative system of numbers. Let 𝜃𝑛, 𝑛 ≥ 1, be a sequence of real numbers, each of which greater than 1. Then any real number 𝛼, 0 < 𝛼 < 1, can be represented in the form 

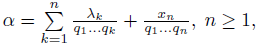
where the sequence 𝑥𝑛 of error terms is defined by recurrence

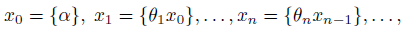
and the sequence of integers 𝜆𝑛 is defined by the rule

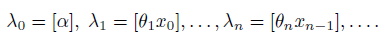
In a broad sense, linkages are constructions made of rigid elements connected in such a way that some of their pairs can rotate around a common point. One of the main tasks related to the study of linkages is the description of possible hinge positions. Important results in this
area are provided by the theorems of King [7], [8] and Kempe [2]. The main result of this paper is the constructive proof of the existence of a linkage that solves the optimization problem, namely the search for the shortest network connecting the boundary of 𝑚 ⩾ 1 points in a space
of dimension 𝑛 ⩾ 2 with the Manhattan metric. This work is a continuation of the author’s previous works[3],[4], which described mechanisms for constructing the shortest network in the Euclidean plane, as well as the minimal parametric network in Euclidean space of dimension 𝑘 ⩾ 2.

Problem of finding minimal parametric fillings of a finite metric space 𝑀 can be reduced to classical linear programming. The set of admissible values of the dual problem is a convex polyhedron Λ𝐺 that depends on the filling type 𝐺, i.e., on a tree, whose set of degree 1 vertices equals 𝑀, and all other vertices have degree 3 (such trees are referred as binary trees connecting 𝑀). Vertices of this polyhedron have an important role in minimal filling weight calculation.Generally speaking, isomorphic binary trees connecting the same space 𝑀 correspond to different polyhedra. In the present paper a complete answer on the relations between such polyhedra is obtained. Besides, the question on the structure of the set 𝑈 obtained as the unionof the vertices of all polyhedra Λ𝐺 over all binary trees connecting a given set 𝑀. This set 𝑈 = 𝑈(𝑚) depends on the number of points 𝑚 in the set 𝑀. It turns out that the set 𝑈(𝑚) is convex for 𝑚 ⩽ 6, i.e., it is a vertex set of a convex polyhedron. Convexity of 𝑈(𝑚) for other 𝑚 is an open question.

The article studies the structure of non-unique solutions of the Fermat–Torricelli problem in normed planes. The problem of the presence of the stability property for such solutions was posed. The results were obtained in the form of necessary and sufficient conditions for the
stability of all solutions for sets of three points in a normed plane. In addition, as an illustration, bifurcation diagrams of solutions were considered and their structure was investigated.

We study magnetic geodesic flows invariant under rotations on the 2-torus. The dynamical system is given by a generic pair of 2𝜋-periodic functions (𝑓, Λ), where the function Λ takes values in a circle if the magnetic field is not exact. Topology of the Liouville fibration of
the given integrable system near its singular orbits and singular fibers is decribed. Types of these singularities are computed. Topology of the Liouville fibration on regular 3-dimensional isoenergy manifolds is described by computing the Fomenko-Zieschang invariant. It is shown that Liouville fibrations for geodesic flow and non-exact magnetic geodesic flow on any isoenergy manifold have different topology. All possible bifurcation diagrams of the momentum maps of such integrable systems are described.

The paper presents a classification of Lie algebras with four-dimensional coadjoint orbits for Lie algebras that are isomorphic to a semidirect sum of a nontrivial semisimple Lie algebra and a nonzero solvable ideal.

In this paper we present the ongoing research on classifying irreducible representations of the following quiver, or rather the digraph (which throughout this paper we denote by A):

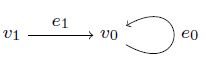
Every representation of A is given by two vector spaces 𝑊0 and 𝑊1, and two homomorphisms 𝜙0 : 𝑊0 → 𝑊0 and 𝜙1 : 𝑊1 → 𝑊0:

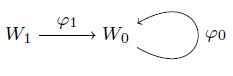
We denote the previous representation by (𝑊1,𝑊0, 𝜙1, 𝜙0). If dim(𝑊0) = 𝑛 and dim(𝑊1) = 𝑚, we may identify 𝑊0 = 𝐾𝑛 and 𝑊1 = 𝐾𝑚, and then 𝜙0 and 𝜙1 are identified respectively with 𝑛 × 𝑛 and 𝑛 × 𝑚 matrices 𝑀0 and 𝑀1, so the above representation is determined by the quadruple (𝑚, 𝑛,𝑀1,𝑀0). We calculate irreducible representations for some 𝑚.

In the paper we prove that, for arbitrary unbounded subset 𝐴 ⊂ 𝑅 and an arbitrary bounded metric space 𝑋, a curve 𝐴 ×ℓ1 (𝑡𝑋), 𝑡 ∈ [0, ∞) is a geodesic line in the Gromov – Hausdorff class. We also show that, for abitrary 𝜆 > 1, 𝑛 ∈ N, the following inequality holds: dist𝐺𝐻 (︀Z𝑛, 𝜆Z𝑛)︀⩾ 1/2 . We conclude that a curve 𝑡Z𝑛, 𝑡 ∈ (0, ∞) is not continuous with respect to the Gromov – Hausdorff distance, and, therefore, is not a gedesic line. Moreover, it follows that multiplication of all metric spaces lying on the finite Gromov – Hausdorff distance from R𝑛
on some 𝜆 > 0 is also discontinous with respect to the Gromov – Hausdorff distance.

The paper studies the class of all metric spaces considered up to zero Gromov – Hausdorff distance between them. In this class, we examine clouds — classes of spaces situated at finite Gromov – Hausdorff distances from a reference space. The paper proves that all clouds are
proper classes. The Gromov – Hausdorff distance is defined for clouds analogous to the case of metric spaces. The paper shows that under certain limitations the distance between the cloud of bounded metric spaces and a cloud with a nontrivial stabilizer is finite. In particular, the distance between the cloud of bounded metric spaces and the cloud containing the real line is calculated.

We classify the simplest 3-dimensional singularities of regular algebraically separable integrable systems. Such systems form an important class of Liouville integrable Hamiltonian systems with two degrees of freedom and occur in many problems of mechanics and geometry.
The techniques elaborated in the paper is based on the analysis of a certain Z2-matrix uniquely determined by the expressions of the initial phase variables via the separating variables.

In the paper relations between average clustering coefficient and global clustering coefficient, closeness, betweenness and stress centralities were proved for simple graphs. Also the theorem about the realtion between average clustering coefficient and radiality is clarified and these
centralities are calculated for 3 classical series of graphs.

The paper studies the inertia tensor of a rigid body in three-dimensional (pseudo-)Euclidean space (𝑉, 𝑔). The configuration manifold 𝑄 of the system is the six-dimensional Lie group E(𝑉, 𝑔) ∼= 𝑉 ⋋ Aut(𝑉, 𝑔) of isometries of this space, and the kinetic energy is a quadratic form 𝑇(𝑤, 𝑎) on the Lie algebra e(𝑉, 𝑔) ∼= 𝑉 + g where g = aut(𝑉, 𝑔). This allows one to define a symmetric operator 𝐽 : g → g* with the property 𝑇(0, 𝑎) = 1/2 (𝐽𝑎, 𝑎), referred to as the (covariant) inertia tensor of the rigid body. To compute this tensor, a “pseudo-Euclidean vector cross product” [, ]𝑔 is introduced in the (pseudo-)Euclidean space (𝑉, 𝑔), and an isomorphism 𝜇 : 𝑉 → g is constructed using this operation. It is proved that this isomorphism transforms the operation [, ]𝑔 into the Lie bracket on the Lie algebra g, and the scalar product into the Cartan–Killing form, up to a scalar factor. Explicit formulas for the operation [, ]𝑔 are obtained.
Using the operation [, ]𝑔, the operator ̃︀ 𝜔 = 𝜇𝜔 ∈ g of instantaneous rotation with angular velocity 𝜔 ∈ 𝑉 is defined. For any point 𝑞 ∈ 𝑉 , the vector 𝑣 = ̃︀ 𝜔𝑞 = [𝜔, 𝑞]𝑔 ∈ 𝑉 of instantaneous velocity, the vector 𝑀(𝑞) = [𝑞,𝑚𝑣]𝑔 ∈ 𝑉 of angular momentum and the inertia operator
̂︀ 𝐽(𝑞) : 𝑉 → 𝑉 , 𝜔 ↦→𝑀(𝑞), are defined. The symmetricity of the inertia operator ̂︀ 𝐽(𝑞) is proved, along with the formula 𝑇(𝑞) = 1/2 𝑔( ̂︀ 𝐽(𝑞)𝜔,𝜔) for the kinetic energy of the point.
Geometric properties of the inertia operator ̂︀ 𝐽 are studied for single- and multi-point bodies.
In particular, in the pseudo-Euclidean case, the restriction of the corresponding quadratic form to the interior of the light cone is shown to be non-negative. Examples of two- and three-point
bodies are constructed showing that there are no additional restrictions on the signature of the inertia operator. All possible signatures of the inertia operator ̂︀ 𝐽 for a rigid body in threedimensional pseudo-Euclidean space are found. It is proved that, for bodies located within the light cone (e.g., “plates” in the Lobachevsky plane), the inertia operator has a signature
of (−,+, +) or (0,+, +). For bodies located outside the light cone, signatures of (−, 𝑠,−) are possible for all 𝑠 ∈ {0,+, −}. The remaining signatures (−,+, 0) and (−, 0, 0) are also realized by two- and three-point bodies.