Неприводимые представления колчанов, ассоциированных с кольцами

Аннотация

В этой статье мы представляем текущие исследования по классификации неприводимых представлений следующего колчана или, скорее, диграфа (который в этой статье мы обозначаем через A):

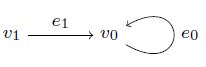
Каждое представление A задается двумя векторными пространствами 𝑊0 и 𝑊1 и двумя гомоморфизмами 𝜙0 : 𝑊0 → 𝑊0 и 𝜙1 : 𝑊1 → 𝑊0:

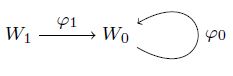
Обозначим предыдущее представление через (𝑊1,𝑊0, 𝜙1, 𝜙0). Если dim(𝑊0) = 𝑛 и dim(𝑊1) = 𝑚, то можно определить 𝑊0 = 𝐾𝑛 и 𝑊1 = 𝐾𝑚, и тогда 𝜙0 и 𝜙1 отождествляются соответственно с 𝑛 × 𝑛 и 𝑛 × 𝑚 матрицами 𝑀0 и 𝑀1, так что указанное представление определяется четырехкратным (𝑚, 𝑛,𝑀1,𝑀0). Вычислим неприводимые представления для некоторого 𝑚.