Рассматриваются биллиарды в трехмерных областях, ограниченных софокусными квадриками, с проскальзыванием на границе. Такие динамические системы являются интегрируемыми по Лиувиллю в кусочно-гладком смысле. В случае двумерных столов класс
биллиардов с проскальзыванием был введен А.Т. Фоменко. Для нескольких типов софокусных биллиардов с проскальзыванием определены классы гомеоморфности поверхностей постоянной энергии, построены бифуркационные диаграммы, описана топология слоения Лиувилля малых окрестностей особых и неособых слоев.

Изучаются двудольные погружения двудольного графа в плоскость с минимальным числом самопересечения. Для некоторых классов двудольных графов вычислено минимальное число самопересечения для всех двудольных погружений. В частности описаны все графы, обладающие двудольным вложением в плоскость. Даны приложения к хронологическому упорядочению начального чекана Ширваншаха Абу Мансур Али ибн Йазида (425–435 гг.х. = 1034–1044 р.х.).

Данная работа посвящена изучению геодезических в классе метрических пространств, наделенных расстоянием Громова–Хаусдорфа. Исследование показывает, что построение линейной геодезической невозможно в общем случае, даже если рассматривать класс Громова – Хаусдорфа, отфакторизованным по нулевым расстояниям. Кроме того, установлено, что оптимальная хаусдорфова реализация разбивает метрические пространства, находящиеся на нулевом расстоянии, на классы эквивалентности с совпадающим пополнением.
Также продемонстрировано, как можно построить геодезическую в примере Хансена, используя 0-модификации. Тем не менее показано, что в общем случае невозможно построение геодезической, используя оптимальную хаусдорфову реализацию. Тем самым показано, что геодезические в классе метрических пространств имеют еще более богатую структуру и на класс метрических пространств не могут быть перенесены методы построения геодезических из пространства Громова – Хаусдорфа.

В работе доказаны теоремы о представлении действительных чисел 𝛼 с помощью бесконечной итерации последовательности положительных монотонных функций 𝛼_𝑛 = 𝑓_𝑛(𝑥_𝑛) в виде

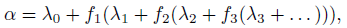
где «цифры» 𝜆𝑛, 𝑛 ≥ 0, и “остатки”

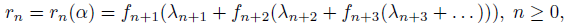
определяются по следующим рекуррентным формулам

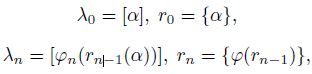
причем {𝑧} и [𝑧] обозначают соответственно дробную и целую части действительного числа 𝑧 и 𝑥𝑛 = 𝜙𝑛(𝛼𝑛), 𝑛 ≥ 1, — обратные функции для 𝛼𝑛 = 𝑓𝑛(𝑥𝑛).
В частности, представление числа 𝛼 с помощью функции 𝑓(𝑥) = 1
𝑥 приводит к цепной дроби для числа 𝛼. Общий случай, когда 𝑓(𝑥) — убывающая функция, был рассмотрен Б. Х. Биссинжером (1944) и А. Реньи (1957). Для функции 𝑓(𝑥) = 𝑥𝑞 при 𝑞 ≥ 2 — натуральном
числе получается 𝑞-адическое представление вида 𝛼 = Σ︀𝜆𝑛𝑞−𝑛, где цифры 𝜆𝑛, 𝑛 ≥ 1, могут принимать все целые значения от 0 до 𝑞 − 1. Случай возрастающей функции 𝑓(𝑥) исследовался С. И. Эвереттом (1946) и А. Реньи (1957). Представление 𝛼 для 𝑓(𝑥) = 𝑥 𝜃 при нецелом 𝜃 > 1 изучалось А. Реньи (1957) и А. О. Гельфондом (1959). В настоящей работе для последовательности функций 𝑓𝑛(𝑥) = 𝑥
𝑞𝑛 , 𝑞𝑛 ≥ 2, — целые числа, исследуется представление 𝛼 по мультипликативной системе чисел при 𝑛 ≥ 1 в виде

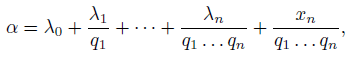
где цифры 𝜆𝑛 могут принимать целые значения от 0 до 𝑞𝑛 − 1. А. Х. Гияси (2007) обобщила теорему Гельфонда, касающуюся мультипликативной системы чисел. Пусть 𝜃𝑛, 𝑛 ≥ 1, — последовательность действительных чисел, каждое из которых больше единицы. Тогда любое действительное число 𝛼, 0 < 𝛼 < 1, может быть представлено в форме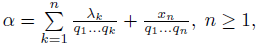

где последовательность 𝑥𝑛 остаточных членов определяется
рекуррентно 

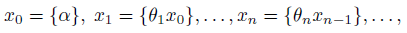
и последовательность целых чисел 𝜆𝑛 определяется по правилу

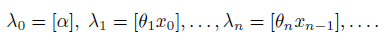
В широком смысле шарнирные механизмы представляют собой конструкции из жёстких элементов, соединённых таким образом, что некоторые их пары могут вращаться вокруг общей точки. Одной из основных задач, связанных с исследованием шарнирных механизмов, является описание возможных положений шарниров. Важными результатами в этой области являются теоремы Кинга [7], [8] и Кемпе [2]. Основным результатом настоящей статьи является конструктивное доказательство существования шарнирного механизма, который решает задачу оптимизации, а именно поиска кратчайшей сети для границы из 𝑚 ⩾ 1 точек в пространстве размерности 𝑛 ⩾ 2 с манхеттенской метрикой. Данная ра-
бота является продолжением предыдущих работ автора [3], [4], в которых были описаны механизмы, строящие кратчайшую сеть на евклидовой плоскости, а также минимальную параметрическую сеть в евклидовом пространстве размерности 𝑘 ⩾ 2.

Задача о поиске минимальных параметрических заполнений конечного метрического пространства 𝑀 сводится к классической задаче линейного программирования. Множество допустимых значений двойственной задачи представляет собой выпуклый многогранник Λ𝐺, который зависит только от типа заполнения 𝐺 — дерева, множество вершин степени 1 которого совпадает с 𝑀, а остальные вершины имеют степень 3 (такие деревья называются бинарными, соединяющими 𝑀). Вершины этого многогранника играют важную роль при вычислении веса минимального заполнения.
Изоморфным бинарным деревьям, соединяющим одно и тоже пространство 𝑀, соответствуют, вообще говоря, разные многогранники. В данной работе получен полный ответ на вопрос о том, как они связаны между собой. Кроме того, в работе обсуждается вопрос об устройстве объединения 𝑈 множеств вершин всех многогранников Λ𝐺, соответствующих всевозможным бинарным деревьям 𝐺, соединяющим данное множество 𝑀. Множество 𝑈 = 𝑈(𝑚) зависит только от количества 𝑚 точек в множестве 𝑀. Оказывается при 𝑚 ⩽ 6 множество 𝑈(𝑚) является выпуклым, то есть представляет собой множество вершин
некоторого выпуклого многогранника. Выпуклость 𝑈(𝑚) при больших 𝑚 — это открытый вопрос.

В статье изучается устройство неединственных решений задачи Ферма –Торичелли в нормированных плоскостях. Была поставлена проблема наличия свойства устойчивости
у таких решений. Получены результаты в виде необходимых и достаточных условий для устойчивости всех решений для наборов из трёх точек в нормированной плоскости. Кроме того, в качестве иллюстрации были рассмотрены бифуркационные диаграммы решений и исследовано их строение.

Изучаются магнитные геодезические потоки, инвариантные относительно вращений, на двумерном торе. Предполагается, что пара 2𝜋-периодических функций (𝑓, Λ), задающая динамическую систему, удовлетворяет условиям общего положения, при этом функция Λ, задающая магнитное поле, принимает значения в окружности, если магнитное поле не является точным. Описана топология слоения Лиувилля данной интегрируемой системы вблизи ее особых орбит и особых слоев, найдены типы этих особенностей. Описана топология слоения Лиувилля на неособых трехмерных изоэнергетических многообразиях путем вычисления инварианта Фоменко – Цишанга. Показано, что слоения Лиувилля
для геодезического потока и для неточного магнитного геодезического потока на любом изоэнергетическом многообразии имеют разную топологию. Описаны все возможные бифуркационные диаграммы отображений момента таких интегрируемых систем.

В работе представлена классификация алгебр Ли с четырехмерными орбитами коприсоединенного представления для алгебр Ли, изоморфных полупрямой сумме нетривиальной полупростой алгебры Ли и ненулевого разрешимого идеала.

В этой статье мы представляем текущие исследования по классификации неприводимых представлений следующего колчана или, скорее, диграфа (который в этой статье мы обозначаем через A):

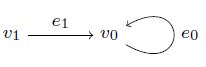
Каждое представление A задается двумя векторными пространствами 𝑊0 и 𝑊1 и двумя гомоморфизмами 𝜙0 : 𝑊0 → 𝑊0 и 𝜙1 : 𝑊1 → 𝑊0:

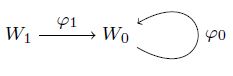
Обозначим предыдущее представление через (𝑊1,𝑊0, 𝜙1, 𝜙0). Если dim(𝑊0) = 𝑛 и dim(𝑊1) = 𝑚, то можно определить 𝑊0 = 𝐾𝑛 и 𝑊1 = 𝐾𝑚, и тогда 𝜙0 и 𝜙1 отождествляются соответственно с 𝑛 × 𝑛 и 𝑛 × 𝑚 матрицами 𝑀0 и 𝑀1, так что указанное представление определяется четырехкратным (𝑚, 𝑛,𝑀1,𝑀0). Вычислим неприводимые представления для некоторого 𝑚.

В данной работе мы показываем, что кривая вида 𝐴 ×ℓ1 (𝑡𝑋), 𝑡 ∈ [0, ∞) для ограниченного пространства 𝑋 и неограниченного подмножества 𝐴 ⊂ R является геодезической в классе Громова – Хаусдорфа. Также мы показываем, что для произвольных 𝜆 > 1,
𝑛 ∈ N выполнено неравенство dist𝐺𝐻 (︀Z𝑛, 𝜆Z𝑛)︀⩾ 1/2 . Отсюда следует, во-первых, что кривая 𝑡Z𝑛, 𝑡 ∈ (0, ∞) не является непрерывной в классе Громова – Хаусдорфа (в частности, не является геодезической), и, во-вторых, что отображение умножения всех пространств на конечном расстоянии Громова – Хаусдорфа от R𝑛 на произвольное 𝜆 > 0 не является непрерывным.

В статье обсуждается класс всех метрических пространств, рассматриваемых с точностью до нулевого расстояния Громова – Хаусдорфа между ними. Этот класс разбивается на облака — классы пространств, лежащих на конечном расстоянии от данного. В работе доказывается, что каждое облако является собственным классом. Между облаками естественно определяется расстояние Громова – Хаусдорфа по аналогии с метрическими пространствами. В работе показано, что при некоторых ограничениях расстояние между облаком ограниченных метрических пространств и облаком с нетривиальной стационарной группой равно бесконечности. В частности, посчитано расстояние между облаком ограниченных метрических пространств и облаком, содержащим вещественную прямую.

Даётся классификация простейших 3-мерных особенностей регулярных алгебраически разделимых интегрируемых систем. Такие системы представляют собой важный класс интегрируемых по Лиувиллю гамильтоновых систем с двумя степенями свободы и встречаются во многих задачах механики и геометрии. Используемая в статье техника основана на анализе некоторой Z_2-матрицы, однозначно определяемой выражениями исходных фа-
зовых переменных через переменные разделения.

В статье доказываются оценки зависимостей между средним кластерным коэффициентом и глобальным кластерным коэффициентом, центральностью по близости, централь-
ностью по посредничеству и центральностью напряжения для простых графов. Также уточняется теорема о зависимости между средним кластерным коэффициентом и радиальной центральностью и проводится подсчет этих центральностей для 3-х бесконечных серий классических графов.

В работе исследуется тензор инерции твердого тела в трехмерном (псевдо-)евклидовом пространстве (𝑉, 𝑔). Конфигурационное многообразие 𝑄 системы — шестимерная группа Ли E(𝑉, 𝑔) ∼= 𝑉 ⋋Aut(𝑉, 𝑔) движений этого пространства, а кинетическая энергия является квадратичной формой 𝑇(𝑤, 𝑎) на алгебре Ли e(𝑉, 𝑔) ∼= 𝑉 + g, где g = aut(𝑉, 𝑔). Это позволяет определить симметрический оператор 𝐽 : g → g* со свойством 𝑇(0, 𝑎) = 1/2 (𝐽𝑎, 𝑎), называемый (ковариантным) тензором инерции твердого тела. Для его вычисления введено «псевдо-евклидово векторное произведение» [, ]𝑔 в (псевдо-)евклидовом пространстве (𝑉, 𝑔) и с помощью этой операции построен изоморфизм 𝜇 : 𝑉 → g. Доказано, что при этом изоморфизме построенная операция [, ]𝑔 преобразуется в скобку Ли на алгебре Ли g, а скалярное произведение — в форму Киллинга – Картана с точностью до скалярного множителя. Получены явные формулы для операции [, ]𝑔.
С помощью построенной операции [, ]𝑔 определен оператор ̃︀ 𝜔
= 𝜇𝜔 ∈ g мгновенного вращения с угловой скоростью 𝜔 ∈ 𝑉 , и для любой точки 𝑞 ∈ 𝑉 определены ее вектор мгновенной скорости 𝑣 = ̃︀ 𝜔𝑞 = [𝜔, 𝑞]𝑔 ∈ 𝑉 , вектор кинетического момента 𝑀(𝑞) = [𝑞,𝑚𝑣]𝑔 ∈ 𝑉 и оператор инерции ̂︀ 𝐽(𝑞) : 𝑉 → 𝑉 , 𝜔 ↦→ 𝑀(𝑞). Доказаны симметричность оператора инерции ̂︀ 𝐽(𝑞) и формула 𝑇(𝑞) = 1/2 𝑔( ̂︀ 𝐽(𝑞)𝜔,𝜔) для кинетической энергии точки.
Изучены геометрические свойства оператора инерции ̂︀ 𝐽 для одноточечных и многоточечных тел. В частности, в псевдо-евклидовом случае ограничение соответствующей квадратичной формы на внутренность светового конуса неотрицательно. Построены примеры 2- и 3-точечных тел, показывающие, что других ограничений на сигнатуру оператора инерции нет. Найдены все возможные сигнатуры для оператора инерции ̂︀ 𝐽 твердого тела в трехмерном псевдо-евклидовом пространстве. Доказано, что для тел, расположенных внутри светового конуса (например, для «тарелок» на плоскости Лобачевского), оператор
инерции имеет сигнатуру (−,+, +) или (0,+, +). Для тел, расположенных снаружи светового конуса, возможны сигнатуры (−, 𝑠,−) для всех 𝑠 ∈ {0,+, −}. Остальные сигнатуры (−,+, 0) и (−, 0, 0) также реализуются 2- и 3-точечными телами.