
Рецензируемый научно-теоретический журнал «Чебышевский сборник» «Chebyshevskii Sbornik» издается с 2001 года, зарегистрирован Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций (Свидетельство о регистрации: ПИ № ФС 77-80049 от 31.12.2020, ISSN - 2226-8383, онлайн ISSN 2587-7119), Журнал индексируется в библиографических и реферативных базах данных RSCI, Scopus, MathSciNet, zbMATH. В соответствии с правилами приравнивания научных журналов, входящих в наукометрические базы данных, к журналам Перечня ВАК с распределением по категориям относится к K1 ВАК.
Периодичность издания - 5 раза в год, тираж - 150 экземпляров.
Распространяется по подписке и предварительному заказу на территории Российской Федерации и за рубежом.
Электронная версия журнала размещена в открытом доступе на Общероссийском портале (http://www.mathnet.ru) и в Научной электронной библиотеке (http://elibrary.ru).
Журнал является общематематическим. Публикуются оригинальные статьи, допускаются статьи большого объема. Журнал охватывает широкий спектр направлений современной математики: теория чисел, алгебра и математическая логика, теория функций вещественного и комплексного переменного, функциональный анализ, дифференциальные уравнения, математическая физика, геометрия и топология, теория вероятностей и математическая статистика, численные методы, теория оптимизации и др. Все статьи проходят рецензирование у ведущих специалистов по данным направлениям.
Журнал индексируется в электронных базах данных Scopus, MathSciNet Американского математического общества и Zentralblatt MATH издательства Springer, Russian Science Citation Index (RSCI) (русская коллекция Web of Science), реферируется РЖ «Математика» (Россия, ВИНИТИ), «Mathematical Reviews» (США, American Mathematical Society).
Плата за публикацию и редакционную подготовку статей с авторов не взимается.
Адрес редакции: г. Тула, пр. Ленина, 125, учебный корпус №4 ТГПУ им. Л. Н. Толстого кафедра алгебры, математического анализа и геометрии (кабинет 310) и редакция «Чебышевского сборника» (кабинет 302а)
Текущий выпуск
Статьи
Одним из направлений анализа временных рядов является исследование их морфологии. Результаты такого исследования используются для обнаружения различного рода
аномалий в поведении ряда, моментов перестройки его поведения и т.д.
В работе представлена программа изучения записей методами ДМА – нового подхода к данным, ориентированного на исследователя и активно использующего нечеткую математику. Исходными данными для него является запись, выражающая процесс с дискретным временем и некоторое свойство процесса, выполнение которого интересно исследователю.
Проявление свойства на записи формализуется в виде нечеткой структуры (меры проявления) на области определения записи, которая выражает степень проявления рассматриваемого свойства. Мера проявления свойства является основой разбиения записи на
регулярное, переходное и аномальное проявление рассматриваемого свойства на записи.
Это разбиение дает исследователю одновременно простое и содержательное представление об интересующем его проявлении свойства на записи.
Целью настоящей работы является совершенствование в рамках ДМА существующего на сегодняшний день такого разложения.
При достаточно легко обозримых ограничениях на нелинейности, без предположения, что они удовлетворяют условию Липшица, методом монотонных (по Браудеру – Минти) операторов доказаны глобальные теоремы о существовании, единственности и оценках решения для трех различных классов неоднородных нелинейных интегральных уравнений, в которые операторы дробного (по Риману – Лиувиллю) интегрирования с переменным внешним коэффициентом входят линейно или нелинейно, либо эти операторы содержат нелинейность под знаком интеграла (уравнения типа Гаммерштейна). В последнем случае существование и единственность решения установлены без условия коэрцитивности на нелинейность. Во всех случаях важную роль играют найденные в работе условия при которых операторы дробного интегрирования с переменным внешним коэффициентом действуют непрерывно из вещественных пространства Лебега 𝐿𝑝(𝑎, 𝑏) в сопряженные с ними пространства и являются строго положительными. Доказанные теоремы в рамках пространства 𝐿2(𝑎, 𝑏) охватывают соответствующие линейные уравнения с интегралами дробного порядка. Из полученных оценок, в частности, непосредственно вытекает, что при условиях доказанных теорем соответствующие однородные линейные и нелинейные интегральные уравнения имеют лишь тривиальное (нулевое) решение.
Приведены следствия, иллюстрирующие основные результаты.
Данная статья посвящена установлению порядка гладкости 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) — наибольшего выпуклого продолжения на [0, 1]𝑛 любой булевой функции 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛). В результате исследования для каждой булевой функции 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛) установлен порядок
дифференцируемости 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) — соответствующего ей наибольшего выпуклого продолжения на [0, 1]𝑛, а именно, во-первых, с обеих сторон оценено наибольшее выпуклое продолжение 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) так, что из чего следует непрерывность 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) на [0, 1]𝑛 для любого натурального 𝑛, а во-вторых, доказано, что если число существенных переменных булевой функции 𝑓𝐵(𝑥1, 𝑥2, ..., 𝑥𝑛) меньше двух, то на [0, 1]𝑛 наибольшее выпуклое продолжение 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) бесконечно дифференцируемо, а если не мень-
ше двух, то на [0, 1]𝑛 наибольшее выпуклое продолжение 𝑓𝑁𝑅(𝑥1, 𝑥2, ..., 𝑥𝑛) не является дифференцируемым, т. е. является лишь непрерывным.
Изучаются полумодули над одноэлементным полукольцом {𝑒}, которое мы называем тривиальным полукольцом. Под полумодулем над тривиальным полукольцом понимается
коммутативная полугруппа ⟨𝐴,+⟩ вместе с отображением 𝑒 : 𝐴 → 𝐴, 𝑎 → 𝑒𝑎, которое: аддитивно, то есть 𝑒(𝑎+𝑏) = 𝑒𝑎+𝑒𝑏 для любых 𝑎, 𝑏 ∈ 𝐴; идемпотентно, то есть 𝑒(𝑒𝑎) = 𝑒𝑎 для всех 𝑎 ∈ 𝐴; 𝑒𝑎+𝑒𝑎 = 𝑒𝑎 для любого 𝑎 ∈ 𝐴. При этом отображение 𝑒 : 𝐴 → 𝐴, или действие
𝑒 на 𝐴, называется ретракцией коммутативной полугруппы ⟨𝐴,+⟩. Для ретракции 𝑒 на 𝐴 множество 𝑒𝐴 будет множеством всех неподвижных точек отображения 𝑒, называемым 𝑒-множеством. Коммутативная полугруппа ⟨𝐴,+⟩ может иметь самые разные ретракции и, соответственно, различные 𝑒-множества. Кроме того, одно и то же множество на полурешетке 𝐴 может служить 𝑒-множеством самых разных ретракций 𝑒 на 𝐴.
На ряде примеров показано, что целесообразно исследовать ретракции на полурешетках ⟨𝐴,+⟩, которые будем называть 𝑒-полумодулями.
Дана некоторая классификация ретракций. Описано строение ретракций цепей. Доказано, что все непустые подмножества произвольной цепи являются 𝑒-множествами тогда и только тогда, когда эта цепь дискретная. Рассмотрены возрастающие, убывающие и линейные ретракции на полурешетках и решетках. Показано, что возрастающие ретракции e и убывающие ретракции 𝑒 однозначно определяются своими 𝑒-множествами.
Получены также другие результаты, приведены соответствующие примеры.
В статье доказаны теоремы о сходимости тригонометрических рядов по простым числам. Мы продолжаем исследования Г. И. Архипова и К. И. Осколкова по специальным тригонометрическим рядам, основанные на методе И. М. Виноградова по оценкам тригонометрических сумм Г.Вейля с многочленом в аргументе тригонометрической функции.
В настоящей работе мы рассматриваем специальные тригонометрические ряды по простым числам трех типов в зависимости от функций в аргументе тригонометрической функции: корень квадратный, линейной и общего многочлена от одной переменной, пробегающей последовательно все простые числа. Здесь мы существенно пользуемся оценками И. М. Виноградова тригонометрических сумм по простым числам.
Отметим то обстоятельство, что возникает необходимость использовать справедливость расширенной гипотезы Римана.
Кроме того, в случае линейных многочленов в аргументе нам потребовалось некоторое улучшение оценок И. М. Виноградова, полученное Р. Воном.
В статье рассмотрены свойства арифметической производной и первообразной на множестве рациональных чисел, получены свойства, связанные с аналогичными свойствами производной функции, изучены некоторые дифференциальные уравнения в арифметических производных и проанализированы свойства их решений.
В статье определен императивный язык программирования, учитывающий аппаратные ограничения вычислителя с набором инструкций RV32I, заданы его синтаксис и аксиоматическая семантика в виде логики Хоара. Необходимость подобного языка определяется невозможностью напрямую применять формальные доказательства, проведенные для программ на языках, не учитывающих аппаратные ограничения, к транслированному коду, исполняющемуся на реальном аппаратном вычислителе. В то же время проведение доказательств для программ, написанных напрямую в кодах вычислителя, чрезвычайно трудоемко. Описанный язык учитывает такие аппаратные ограничения, как конечная ширина регистра, конечный объем памяти и использование арифметики по модулю вместо классической арифметики. В статье приведен пример программы вычисления НОД двух неотрицательных целых чисел, написанной на этом языке, а также доказательство ее корректности. Таким образом, продемонстрировано, что можно строить формальные доказательства для программ на языке, учитывающем некоторые аппаратные ограничения, и эти доказательства будут сопоставимы по сложности с теми, что построены для аналогичных программ на не учитывающих эти ограничения императивных языках. Одним из направлений развития работы является построение алгоритма трансляции из определенного в статье языка в коды вычислителя и доказательство корректности этого алгоритма.
Доказано, что если решётка конгруэнций унара удовлетворяет нетривиальному решёточному тождеству, то унар является гомоморфным образом копроизведения конечного числа прямых и лучей, а это, в свою очередь, равносильно тому, что унар имеет лишь
конечное число компонент связности, узлов, начальных элементов, и входная степень каждого элемента унара конечна.
В настоящей статье продолжены исследования некоторых арифметических свойств рядов Фарея с помощью метода, созданного Ф. Бока, К. Кобели и А. Захареску (2001).
Пусть Φ𝑄 — классический ряд Фарея порядка 𝑄. Задавшись фиксированными числами 𝐷 ⩾ 2 и 0 ⩽ 𝑐0 ⩽ 𝐷 − 1, пометим красным цветом все дроби в Φ𝑄, знаменатели которых ≡ 𝑐0 (mod𝐷). Рассмотрим далее промежутки в Φ𝑄 с окрашенными концами, внутри которых нет других окрашенных дробей, т. е. дробей 𝑎/𝑞 с условием 𝑞 ≡ 𝑐0 (mod𝐷). Какова предельная (при 𝑄 → +∞) доля 𝜈(𝑟;𝐷, 𝑐0) промежутков, внутри которых имеется в
точности 𝑟 неокрашенных дробей, в общем числе таких промежутков (𝑟 = 0, 1, 2, 3, . . .)?
По сути, выражение для такой доли может быть получено из общих результатов, принадлежащих К. Кобели, М. Выжийту и А. Захареску (2012). Однако такое выражение для 𝜈(𝑟;𝐷, 𝑐0) представляет собой сумму площадей некоторых многоугольников, определяемых посредством специального геометрического преобразования. В настоящей статье мы получаем явные выражения для таких долей 𝜈(𝑟;𝐷, 𝑐0) для случаев 𝐷 = 3 и 𝑐0 = 1, 2. Тем самым с учётом предыдущей работы автора (2023) случай разности 𝐷 = 3 оказывается изученным полностью.
Решение начально-краевых задач для уравнения теплопроводности представляется в виде разложения в ряд полиномов Эрмита. Для задачи Коши и ретроспективной задачи
Коши найдены коэффициенты разложения решения в ряды по полиномам Эрмита. Исследована связь преобразования Лапласа и рядов по полиномам Эрмита. Найдена новая формула обращения интегрального преобразования Лапласа по значениям изображения на действительной полуоси. Функция оригинал строится как сумма квазистепенного ряда. Получена формула для изображения Лапласа в виде суммы квазистепенного ряда. Решена
задача восстановления температурного поля неограниченного стержня по его моментам.
В работе даётся определение равномерного распределения в единичном 𝑠-мерном кубе последовательности вложенных обобщенных параллелепипедальных сеток II типа с весовой функцией. Кроме того, даётся определение равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности сеток 𝑀𝑛 с весовой функцией.
Даётся доказательство аналога обобщённого критерия Г. Вейля об необходимых и достаточных условиях равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности сеток 𝑀𝑛 с весами.
Так как определение равномерного распределения последовательности вложенных обобщенных параллелепипедальных сеток II типа с весовой функцией отличается от определения равномерного распределения последовательности сеток 𝑀𝑛 с весовой функцией, то в работе доказывается второй аналог критерия Вейля о необходимых и достаточных условиях равномерного распределения в единичном 𝑠-мерном кубе 𝐺𝑠 последовательности вложенных обобщенных параллелепипедальных сеток II типа.
Доказана следующая теорема:
Теорема 1. Пусть ряд Фурье функции 𝑓(⃗𝑥) сходится абсолютно, 𝐶(⃗𝑚) — ее коэффициенты Фурье и 𝑆𝑀,⃗𝜌(⃗𝑚) — тригонометрические суммы сетки с весами, тогда справедливо равенство
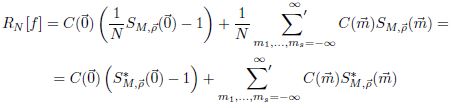
и при 𝑁 → ∞ погрешность 𝑅𝑁[𝑓] будет стремиться к нулю тогда и только тогда, когда взвешенные узлы квадратурной формулы равномерно распределены в единичном 𝑠–мерном
кубе.
Воспользовавшись вторым моментом 𝐿-функций Дирихле на критической прямой в больших дугах M(L𝑏), 𝜏 = 𝑦3𝑥−1L−𝑏1 , за исключением малой окрестности центров этих дуг |𝛼 − 𝑎
𝑞 | > (8𝜋𝑦2)−1 при 𝑦 ⩾ 𝑥^1− 1/(9−4√2)L𝑐2 , 𝑐2 =2𝐴+24+(√2−1)𝑏1/2√2−1, получена оценка: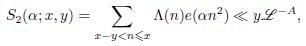
а в малой окрестности |𝛼 − 𝑎𝑞 | ⩽ (8𝜋𝑦2)−1 центра больших дуг M(L𝑏) для 𝑆2(𝛼; 𝑥, 𝑦) при 𝑦 ⩾ 𝑥^5/8 L1,5𝐴+0,25𝑏+18 получена асимптотическая формула с остаточным членом, где 𝐴, 𝑏1,
𝑏 — произвольные фиксированные положительные числа, L = ln 𝑥𝑞.
Для достаточно больших целых чисел 𝐾, 𝑥, 𝑦, 𝑞 при условии 𝐾 ⩽ 𝑦 < 𝑥, 𝑛 — фиксированное натуральное число, 𝛼 — вещественное,
⃒𝛼 − 𝑎/𝑞|⩽ 1/𝑞2 , (𝑎, 𝑞) = 1, 𝑞 ⩾ 1, получена оценка вида
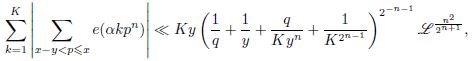
что является усилением и обобщением теоремы И. М. Виноградова о распределении дробных частей {𝛼𝑝}.
Работа посвящена абелевым группам, содержащим хотя бы один эндоморфизм, ядро которого совпадает с его образом. Заметим, что условие ker𝜙 = Im 𝜙 влечет за собой равенство 𝜙^2 = 0, то есть 𝜙 является нильпотентным эндоморфизмом индекса нильпотентности 2.
Основным техническим результатом работы является теорема 1, в которой на языке подгрупп получен критерий существования эндоморфизма абелевой группы, ядро которого совпадает с его образом.
В этой статье существование эндоморфизма, ядро которого совпадает с его образом, полностью решено для абелевых групп из классов циклических и коциклических групп, элементарных 𝑝-примарных абелевых групп и конечно порожденных абелевых групп.
Главным результатом работы является теорема 12, в которой доказано, что конечно порожденная абелева группа 𝐴 обладает эндоморфизмом, образ которого совпадает с его ядром тогда и только тогда, когда либо 𝐴 — конечная группа, порядок которой является полным квадратом, либо 𝐴 = 𝐹 ⊕ 𝐾, где 𝐹 — свободная абелева группа четного ранга, а 𝐾 — произвольная конечная абелева группа.
В данной статье представлена концепция индекса слов Фибоначчи FWI, нового топологического индекса, полученного на основе индекса Альбертсона, применительно к деревьям, построенным из слов Фибоначчи. Опираясь на классическую последовательность
Фибоначчи и ее обобщения, мы исследуем структурные свойства деревьев из слов Фибоначчи и меры их нерегулярности, основанные на степенях. Мы определяем FWI и его варианты, включая полную нерегулярность и модифицированный индекс слов Фибоначчи, где он определяется как
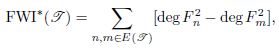
и устанавливаем фундаментальные неравенства, связывающие эти индексы с максимальной степенью нижележащих деревьев. Наши результаты распространяют известные инварианты графов на комбинаторику слов Фибоначчи, позволяя по-новому взглянуть на
их алгебраические и топологические характеристики. Кроме того, мы приводим аналитические выражения для чисел Фибоначчи и их порождающих функций, подкрепленные формулой Бине, чтобы облегчить вычисление этих индексов. Теоретические разработки
иллюстрируются примерами, включая подробные конструкции словесных деревьев Фибоначчи и их степенных распределений. Данная работа открывает возможности для дальнейшего изучения инвариантов графов на основе слов и их применения в комбинаторике и теоретической информатике.
В нашей статье мы изучаем индекс Альбертсона и сигма-индекс в деревьях, заданных степенными последовательностями, и ввели нерегулярность индекса Альбертсона и сигма-индекса для последовательностей степени(2,3,4), подкрепив это набором иллюстративных примеров получения общего соотношения в виде:
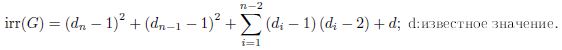
История математики и приложений
Работа посвящена истории отношений математики и ее приложений в гуманитарной области, в данном случае с экономическими науками, лингвистикой, литературоведением, историей. Общепризнанно, что роль математики в гуманитарной области, где неизменно присутствует человек с его эмоциями, предпочтениями, настроениями и другими проявлениями человеческого духа, может быть полезной в вычислительном и статистическом аспекте. Главный вопрос заключается в том, насколько продуктивной может быть роль математики, можно ли ожидать от математических методов принципиально новых
результатов? Рассмотрение воздействия математики на различные гуманитарные науки убеждает в положительном ответе на этот вопрос. Мера применения математики является предельно широкой: от точности и четкости понятийного аппарата, проникновения «математического духа» до решения проблем по эталонам строгости и логической отточенности, принятым в самой математике, от количественных методов до качественных моделей.
В статье рассматривается актуальная проблема интеграции технологий искусственного интеллекта в образовательный процесс, в частности, при изучении математических дисциплин. На основе анализа научных исследований авторы приходят к выводу о том, что в условиях трансформации образования интеллектуальные технологии активно внедряются в учебный процесс, а рост интереса к их применению в обучении подтверждается данными статистики инструмента «Яндекс.Вордстат». Анализ решений математической задачи различными генеративными системами показал, что универсальные модели (ChatGPT, GigaChat, YandexGPT) часто допускают логические и вычислительные ошибки, тогда как
специализированные системы (MathGPT, Mathos AI, Photomath) демонстрируют высокую точность решений. На основе данных анализа авторы подчеркивают необходимость развития у студентов критического мышления и навыков цифровой грамотности. С целью развития указанных качеств предложены некоторые методические подходы: сравнительный анализ решений, дискуссии о границах доверия к искусственному интеллекту, намеренное использование ошибочных ответов сервисов искусственного интеллекта как учебного материала. Авторы также останавливаются на этических проблемах использования технологий искусственного интеллекта в качестве вспомогательного инструмента, а не источника готовых решений.
Рассматривается задача дифракции плоского звукового импульса давления на бесконечном сплошном круговом многослойном цилиндре, состоящем из произвольного числа однородных изотропных упругих коаксиальных цилиндрических слоев различной толщины. Импульс, распространяясь в идеальной жидкости, падает на цилиндрическое тело параллельно его образующей. Определяется звуковое давление в рассеянной телом волне.
Компоненты вектора смещений и тензора напряжений в каждом однородном элементе многослойного тела выражаются через скалярный и векторный потенциалы упругих смещений. Искомое давление в жидкости, скалярный потенциал и единственная ненулевая компонента векторного потенциала упругих смещений удовлетворяют волновым уравнениям. Их решения отыскиваются при нулевых начальных условиях, условиях непротекания на соприкасающейся с жидкостью поверхности тела, условиях жесткого сцепления на поверхностях, разделяющих однородные элементы тела, условии затухания рассеянной звуковой волны и условии ограниченности волнового поля в цилиндре.
Для решения задачи используется интегральное преобразование Лапласа по времени. В пространстве изображений искомые давление и потенциалы представляются в виде разложений в ряды по цилиндрическим базисным решениям уравнения Гельмгольца с
учетом условий излучения на бесконечности и ограниченности. Входящие в ряды неизвестные коэффициенты определяются из системы линейных алгебраических уравнений, записанной для каждого индекса суммирования и полученной путем подстановки изображений решений в изображения граничных условий. Переход в пространство оригиналов осуществлен численно. С использованием ранее полученного авторами решения задачи
о рассеянии плоского акустического импульса давления однородным упругим цилиндром с непрерывно-неоднородным упругим покрытием показана возможность математического моделирования такого покрытия многослойным покрытием в нестационарной задаче дифракции звука.
Рассматривается задача рассеяния плоской звуковой волны на изотропном, линейно-упругом теле, представленном неструктурированной полигональной сеткой. Проблема исследуется в контексте акустики и эластодинамики. Предлагается эффективный алгоритм на основе метода граничных элементов (BEM) и коллокации для вычисления потенциала рассеянной волны. Основные сложности реализации включают неединственность граничного уравнения, сингулярность интегралов и заполненность матрицы системы. Для их
преодоления используются комбинированное уравнение Бертона – Миллера, регуляризация с помощью тождеств для функции Грина и разбиение меша на области Вороного.
Метод позволяет снизить вычислительные затраты по сравнению с методом конечных элементов (FEM), так как требует разбиения только поверхности объекта. Для валидации разработанного подхода проводится сравнение с аналитическим решением для шара, а также с численными решениями для сложных тел, полученными в COMSOL. Показано, что предложенный алгоритм позволяет эффективно рассчитывать акустические поля для
изотропных тел произвольной формы, представленных полигональными сетками.
В связи с повышением среднего возраста населения страны растет потребность в операциях по замене суставов, восстановлению опорно-двигательного аппарата и в области стоматологии. Основное лечение этих заболеваний связано с использованием имплантатов для замены или усиления пораженной костной ткани. Металлические материалы являются наиболее востребованными благодаря сочетанию высоких механических свойств и коррозионной стойкости. Эффективность от использования имплантатов зависит от нескольких факторов – биохимической, биомеханической и гистологической совместимости. Биомеханическая совместимость определяется соответствием модулей упругости костной ткани и вживляемой конструкции. Среди новых металлических сплавов для имплантации выделяется никелид титана – TiNi, обладающий наиболее низким модулем Юнга. Создание пористых материалов может еще больше сблизить значения упругих констант материала имплантатов и костной ткани и, кроме того, обеспечить хорошую интеграцию имплантата
с костными структурами. Для создания пористого никелида титана предложено использовать методы порошковой металлургии. Порошок TiNi, полученный гидридно-кальциевым восстановлением, подвергается спеканию по разным температурно-временным режимам – температуры варьировали от 900 до 1290 °С, продолжительность – от 10 до 360 мин. Реализовано 24 режима спекания и получены образцы с разной пористостью. Статистическая обработка полученных результатов показала, что фактор продолжительности спекания не влияет в исследованном диапазоне времен. Зависимость пористости от температуры спекания описывается экспоненциальным уравнением. Показано, что пористость слабо меняется вплоть до температур 1200 °С, а при более высоких температурах спекания резко снижается до минимальных значений. Результаты исследования показали, что получение образцов TiNi с разной пористостью потребует точного соблюдения температурного режима спекания. При этом временной фактор не играет существенной роли в изменении пористости.
Данная статья посвящена 110-летию со дня рождения выдающегося математика с мировым именем академика Юрия Владимировича Линника и его дискретному эргодическому методу в теории чисел. Сначала приводятся биографические сведения о Ю.В. Линнике. Затем после краткого изложения необходимых сведений из арифметики кватернионов, включая теорию поворотов кватернионов, построенную Б. А. Венковым, рассматривается сама идея дискретного эргодического метода (далее ДЭМ), принадлежащая Ю.В. Линнику.
Следующая часть статьи посвящена изложению эргодической теоремы в случае кватернионов и ее применению к вопросу об асимптотике целых точек по областям на сфере при растущем радиусе.
После этого рассматриваются применения ДЭМ к неопределенным тернарным квадратичным формам, соответствующим случаям распределения целых точек на гиперболоидах, при этом вместо кватернионов используется аппарат арифметики матриц второго
порядка. Изложение статьи завершается постановкой некоторых нерешенных задач, связанных с применениями ДЭМ, и списком литературы.
В статье рассматривается задача об отражении плоской гармонической звуковой волны от плоской поверхности, имеющей выступ цилиндрической формы. Полагается, что плоская поверхность и поверхность выступа являются абсолютно жесткими. Падающая плоская звуковая волна распространяется перпендикулярно образующей цилиндрического выступа в полупространстве, заполненном однородной идеальной сжимаемой жидкостью.
Аналитическое решение задачи получено интегральным методом наименьших квадратов. Решение ищется в виде усеченного ряда по волновым цилиндрическим функциям.
Для выполнения граничных условий на плоской поверхности и цилиндрическом выступе построен функционал, и найдено приближенное решение, его минимизирующее. Представлены результаты численных расчетов диаграмм направленности отраженного акустического поля в дальней зоне.
Краткие сообщения
Работа посвящена исследованию класса клеточных автоматов. Автомат описывает эволюцию на дискретной плоскости. Заданы правила перехода к следующему состоянию.
Проведено исследование стандартных вопросов для подобных эволюционных автоматов, существование неумирающих конфигураций а также периодических эволюций. Найден критерий на правила перехода, при котором существует неумирающая конфигурация. Показано, что в случае симметричных шаблонов периодические эволюции могут иметь только период 2.
В перспективе возможно более глубокое описание различных эволюций, которые может давать заданный фиксированный набор правил (шаблон).
В статье приводятся оценки многочлена от лакунарного ряда с 𝑞-базисными коэффициентами.
Статья продолжает описание направлений исследования арифметических свойств значений рядов вида
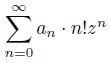
с коэффициентами 𝑎𝑛, удовлетворяющими определённым условиям. При этих условиях рассматриваемый ряд, отличный от многочлена, сходится в поле C только при 𝑧 = 0.
Однако для почти всех, кроме конечного числа, простых чисел 𝑝 такой ряд сходится в полях Q𝑝. Поэтому есть два естественных пути исследования. Мы можем рассматривать либо значения результата некоторого суммирования этого ряда, либо его значения в поле
Q𝑝. В статье формулируются гипотезы, относящиеся к значениям рассматриваемых рядов как в одном, так и в другом случае.






























