Irreducible representations of quivers associated to rings

Abstract

In this paper we present the ongoing research on classifying irreducible representations of the following quiver, or rather the digraph (which throughout this paper we denote by A):

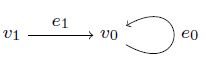
Every representation of A is given by two vector spaces 𝑊0 and 𝑊1, and two homomorphisms 𝜙0 : 𝑊0 → 𝑊0 and 𝜙1 : 𝑊1 → 𝑊0:

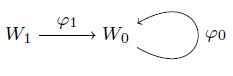
We denote the previous representation by (𝑊1,𝑊0, 𝜙1, 𝜙0). If dim(𝑊0) = 𝑛 and dim(𝑊1) = 𝑚, we may identify 𝑊0 = 𝐾𝑛 and 𝑊1 = 𝐾𝑚, and then 𝜙0 and 𝜙1 are identified respectively with 𝑛 × 𝑛 and 𝑛 × 𝑚 matrices 𝑀0 and 𝑀1, so the above representation is determined by the quadruple (𝑚, 𝑛,𝑀1,𝑀0). We calculate irreducible representations for some 𝑚.