Representations for real numbers

Abstract

In this paper theorems on the representations of real numbers 𝛼 by using infinite iteration of a sequence of positive monotonic functions 𝛼𝑛 = 𝑓_𝑛(𝑥_𝑛) in the form

where “digits” 𝜆_𝑛, 𝑛 ≥ 0, and “remainders”

are defined by the following recurrent formulas

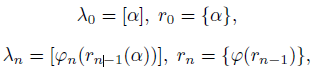
moreover {𝑧} and [𝑧] denote accordingly the fractional and the integral parts of the real number 𝑧, and 𝑥𝑛 = 𝜙𝑛(𝛼𝑛), 𝑛 ≥ 1, are inverse functions of 𝛼𝑛 = 𝑓𝑛(𝑥𝑛).

In particular, the representation of the number 𝛼 by using function 𝑓(𝑥) = 1/𝑥 leads to the continued fraction of the number 𝛼. The general case when 𝑓(𝑥) is decreasing function have been considered by B.H. Bissinger (1944) and A. R´enyi (1957). For the function 𝑓(𝑥) = 𝑥
𝑞 as 𝑞 ≥ 2 is the natural number, is obtained 𝑞-adic the representation of the form 𝛼 = Σ︀ 𝜆𝑛𝑞−𝑛, where digits 𝜆𝑛, 𝑛 ≥ 1, can to receive all integral values from 0 to 𝑞 − 1. The case when 𝑓(𝑥) is increasing
function have been investigated by C.I. Everett (1946) and A. R´enyi (1957). The representation 𝛼 for 𝑓(𝑥) = 𝑥 𝜃 is nonintegral number 𝜃 > 1 have been studied A. R´enyi (1957) and A.O. Gelfond (1959). In the present paper for the sequence of functions 𝑓𝑛(𝑥) = 𝑥 𝑞𝑛 , 𝑞𝑛 ≥ 2, are
integer, has been investigated the representation of 𝛼 on the multiplicative system of numbers as 𝑛 ≥ 1 in the form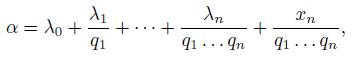

where digits 𝜆𝑛 can to receive integral values from 0 to 𝑞𝑛 − 1.

A. Kh. Ghyasi (2007) has been generalized Gelfond theorem concerning the multiplicative system of numbers. Let 𝜃𝑛, 𝑛 ≥ 1, be a sequence of real numbers, each of which greater than 1. Then any real number 𝛼, 0 < 𝛼 < 1, can be represented in the form 

where the sequence 𝑥𝑛 of error terms is defined by recurrence

and the sequence of integers 𝜆𝑛 is defined by the rule