Представления действительных чисел

Аннотация

В работе доказаны теоремы о представлении действительных чисел 𝛼 с помощью бесконечной итерации последовательности положительных монотонных функций 𝛼_𝑛 = 𝑓_𝑛(𝑥_𝑛) в виде

где «цифры» 𝜆𝑛, 𝑛 ≥ 0, и “остатки”

определяются по следующим рекуррентным формулам

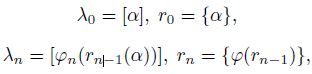
причем {𝑧} и [𝑧] обозначают соответственно дробную и целую части действительного числа 𝑧 и 𝑥𝑛 = 𝜙𝑛(𝛼𝑛), 𝑛 ≥ 1, — обратные функции для 𝛼𝑛 = 𝑓𝑛(𝑥𝑛).
В частности, представление числа 𝛼 с помощью функции 𝑓(𝑥) = 1
𝑥 приводит к цепной дроби для числа 𝛼. Общий случай, когда 𝑓(𝑥) — убывающая функция, был рассмотрен Б. Х. Биссинжером (1944) и А. Реньи (1957). Для функции 𝑓(𝑥) = 𝑥𝑞 при 𝑞 ≥ 2 — натуральном
числе получается 𝑞-адическое представление вида 𝛼 = Σ︀𝜆𝑛𝑞−𝑛, где цифры 𝜆𝑛, 𝑛 ≥ 1, могут принимать все целые значения от 0 до 𝑞 − 1. Случай возрастающей функции 𝑓(𝑥) исследовался С. И. Эвереттом (1946) и А. Реньи (1957). Представление 𝛼 для 𝑓(𝑥) = 𝑥 𝜃 при нецелом 𝜃 > 1 изучалось А. Реньи (1957) и А. О. Гельфондом (1959). В настоящей работе для последовательности функций 𝑓𝑛(𝑥) = 𝑥
𝑞𝑛 , 𝑞𝑛 ≥ 2, — целые числа, исследуется представление 𝛼 по мультипликативной системе чисел при 𝑛 ≥ 1 в виде

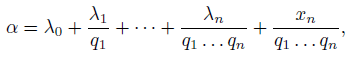
где цифры 𝜆𝑛 могут принимать целые значения от 0 до 𝑞𝑛 − 1. А. Х. Гияси (2007) обобщила теорему Гельфонда, касающуюся мультипликативной системы чисел. Пусть 𝜃𝑛, 𝑛 ≥ 1, — последовательность действительных чисел, каждое из которых больше единицы. Тогда любое действительное число 𝛼, 0 < 𝛼 < 1, может быть представлено в форме

где последовательность 𝑥𝑛 остаточных членов определяется
рекуррентно 

и последовательность целых чисел 𝜆𝑛 определяется по правилу