On rational approximations of a singular integral on a segment by Abel — Poisson sums
https://doi.org/10.22405/2226-8383-2024-25-5-140-163
Abstract
Rational approximations on the segment [−1, 1] are studied of singular integrals of the form
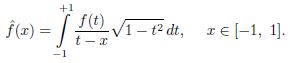
The approximation apparatus is the Abel – Poisson sums of rational integral Fourier operators –
Chebyshev associated with a system of rational Chebyshev – Markov functions, with an arbitrary
fixed number of geometrically different poles. An integral representation of the approximations
is established. In the case when the density of the singular integral has a power-law singularity,
estimates are found pointwise approximations, uniform approximations with a certain majorant,
its asymptotic expression and optimal values of parameters at which the majorant has the highest rate of decrease.
A consequence of the results obtained are estimates of approximations of singular integrals with density having a power-law singularity by Abel – Poisson sums of the polynomial Fourier – Chebyshev series.
Estimates of approximations of singular integrals with a density satisfying the Lipschitz condition on the segment [−1, 1] by Abel – Poisson sums of the polynomial Fourier series – Chebyshev are established. The peculiarity of the estimates found is their dependence on the position of the point on the segment. Moreover, at the ends of the segment, the speed is higher than in the whole segment.
It is established that the classes of studied singular integrals with a density having a powerlaw
singularity in some cases reflect the features of rational approximation in the sense that with a special choice of the velocity parameters of uniform rational approximations they turn out to be higher than the corresponding polynomial analogues.
About the Author
Pavel Gennad’evich PotseikoBelarus
candidate of physical and mathematical sciences
References
1. Gakhov, F. D. 1958, “Boundary value problems”, M.: State Publishing House of Physics and Mathematics. lit., 543 p., (in russian).
2. Muskhelishvili, N. I. 1968, “Singular integral equations. 3rd ed”, M.: Science, 513 p., (in russian).
3. Motorny, V.P., 2001, “Approximation of some classes of singular integrals by algebraic
4. polynomials”, Ukr. mat. Journal, vol. 53, no. 3, pp. 331-345, (in russian).
5. Elliott, D., Paget, D., 1975, “On the convergence of a quadrature rule for evaluating certain
6. Cauchy principal value integrals” Numer. Math., vol. 23, no 4. pp. 311-319.
7. Sheshko, M. A., 1976, “On the convergence of quadrature processes for a singular integral”, Izv. vuzov. Matem., no. 12, pp. 108-118, (in russian).
8. Hubezhty, Sh. S., 2008, “Quadrature formulas for singular integrals with Cauchy kernel”,
9. Vladikavkazsky math. Jour., vol. 10, no. 4, pp. 61-75, (in russian).
10. Sahakyan, A. V., 2002, “Quadrature formulas of the Gauss type for singular integrals”,
11. «Problems of mechanics of thin deformable bodies», dedicated to the 80th anniversary of
12. Academician S.A.Ambartsumyan. Yerevan, pp. 259-265, (in russian).
13. Gabdulkhaev, B. G., 1980, “Finite-dimensional approximations of singular integrals and direct methods for solving special integral and integro-differential equations”, Results of science and technology. Mat. anal., vol. 18, pp. 251-307, (in russian).
14. Rusak, V.N., 1993, “Uniform rational approximation of singular integrals”, Izv. NAS of Belarus. Ser. phys.-mat. sciences, no. 2, pp. 22–26, (in russian).
15. Boksha, A. N. 1997, “Approximation of singular integrals by rational functions in a uniform
16. metric”, Vestn. Bel. gos. un. Ser. 1, Phys. Mat. Inf., no. 3, pp. 68-71, (in russian).
17. Rusak, V. N., Uasis, A. H., 2009, “Rational approximation of singular integrals with differentiable density”, Izv. BSPU. Ser 3. Phys. Math. Inf. Biol. Geogr., no. 1(59), pp. 8-11, (in russian).
18. Potseiko, P. G., Rovba, E. A., 2024, “Approximations of one singular integral on an interval by Fourier– Chebyshev rational integral operators”, Sb. Math., vol. 215, no. 7, pp. 953–992.
19. Rovba, E. A., 1979, “On one direct method in rational approximation”, Dokl. AN OF the BSSR, vol. 23, no. 11, pp. 968-971, (in russian).
20. Natanson, I.P., 1950, “On the order of approximation of a continuous 2𝜋-periodic function using its Poisson integral” Reports of the USSR Academy of Sciences, vol. 72, no. 1, pp. 11-14, (in russian).
21. Timan, A. F., 1950, “An accurate estimation of the remainder when approximating periodic differentiable functions by Poisson integrals”, Reports of the USSR Academy of Sciences vol. 74, no. 1, pp. 17-20, (in russian).
22. Zhuk, V. V., 1968, “On the order of approximation of a continuous 2𝜋-periodic function using Feyer and Poisson averages of its Fourier series”, Mathematical Notes, vol. 4, no. 1, pp. 21-32, (in russian).
23. Stark, E. L., 1973, “Complete asymptotic decomposition for the upper face of the deviation of functions from Lip 1 from the singular integral of Abel – Poisson”, Mathematical notes, vol. 13, no. 1. pp. 21–28, (in russian).
24. Rusetsky, Yu. I., 1968, “On the approximation of continuous functions on a segment by Abel – Poisson sums”, Siberian Mathematical Journal vol. 9, no. 1, pp. 136-144, (in russian).
25. Zhigallo, T. V., 2018, “Approximation of functions satisfying the Lipschitz condition on a finite segment of the real axis by Poisson – Chebyshev integrals”, Problems of management and computer science, vol. 3. pp. 1-14, (in russian).
26. Kitbalyan, A. A., 1963, “Decompositions by generalized trigonometric systems”, Izvestiya AN ASSR, Vol. XVI, no. 6, pp. 3-24, (in russian).
27. Djrbashyan, M. M., 1956, “On the theory of Fourier series for rational functions”, Izvestiya AN of the Armenian SSR, Ser. matematika, vol. 9, no. 7, pp. 1-27, (in russian).
28. Potseiko, P. G., Rovba, E. A., 2021, “On rational Abel – Poisson sums on a segment and
29. approximation of Markov functions”, Journal of the Belarusian State University. Mathematics.
30. Computer science, vol. 3, pp. 6-24, (in russian).
31. Lungu, K. N., 1971 “On the best approximations by rational functions with a fixed number of poles”, Mathematical collection, vol. 86(128), no 2(10), pp. 314-324, (in russian).
32. Lungu, K. N., 1984, “On the best approximations by rational functions with a fixed number of poles”, Siberian Mathematical Journal, vol. 15, no. 2, pp. 151-160.
33. Rusak, V. N., 1979, “Rational functions as an approximation apparatus”, Mn.: BSU, 178p.
Review
For citations:
Potseiko P.G. On rational approximations of a singular integral on a segment by Abel — Poisson sums. Chebyshevskii Sbornik. 2024;25(5):140-163. (In Russ.) https://doi.org/10.22405/2226-8383-2024-25-5-140-163





























