О рациональных аппроксимациях одного сингулярного интеграла на отрезке суммами Абеля – Пуассона

Изучаются рациональные аппроксимации на отрезке [−1, 1] сингулярных интегралов вида

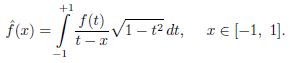Аппаратом приближений являются суммы Абеля – Пуассона рациональных интегральных операторов Фурье – Чебышёва, ассоциированные с системой рациональных функций Чебышёва – Маркова, с произвольным фиксированным количеством геометрически-различных полюсов. Установлено интегральное представление приближений. В случае, когда плотность сингулярного интеграла имеет степенную особенность, найдены оценки поточечных приближений, равномерных приближений с определенной мажорантой, ее асимптотическое выражение и оптимальные значения параметров, при которых мажоранта имеет наибольшую скорость убывания.
Следствием полученных результатов являются оценки приближений сингулярных интегралов с плотностью, имеющей степенную особенность, суммами Абеля – Пуассона полиномиального ряда Фурье – Чебышёва.
Получены оценки приближений сингулярных интегралов с плотностью, удовлетворяющей на отрезке [−1, 1] условию Липшица, суммами Абеля – Пуассона полиномиального ряда Фурье – Чебышёва. Особенностью найденных оценок является их зависимость от положения точки на отрезке. Причем на концах отрезка скорость является выше, чем в целом на отрезке.
Установлено, что классы изучаемых сингулярных интегралов с плотностью, имеющей степенную особенность, в некоторых случаях отражают особенности рациональной аппроксимации в том смысле, что при специальном выборе параметров скорости равномерных рациональных приближений оказываются выше соответствующих полиномиальных аналогов.

1. Гахов Ф. Д. Краевые задачи // М.: Гос. изд-во физ.-мат. лит-ры, 1958. 543 с.

2. Мусхелишвили Н. И. Сингулярные интегральные уравнения. 3-е изд. // М.: Наука, 1968. 513 с.

3. Моторный В. П. Приближение некоторых классов сингулярных интегралов алгебраическими многочленами // Укр. мат. жур. 2001. Т. 53, № 3. С. 331-345.

4. Elliott D., Paget D. On the convergence of a quadrature rule for evaluating certain Cauchy

5. principal value integrals // Numer. Math. 1975. Vol. 23, № 4. P. 311-319.

6. Шешко М. А. О сходимости квадратурных процессов для сингулярного интеграла // Изв. вузов. Матем. 1976. № 12. С. 108-118.

7. Хубежты Ш.С. Квадратурные формулы для сингулярных интегралов с ядром Коши //

8. Владикавказский матем. жур. 2008. Т. 10, № 4. С. 61-75.

9. Саакян А. В. Квадратурные формулы типа Гаусса для сингулярных интегралов // Проблемы механики тонких деформируемых тел, посв. 80-летию акад. С. А. Амбарцумяна. Ереван. 2002. C. 259-265.

10. Габдулхаев Б. Г. Конечномерные аппроксимации сингулярных интегралов и прямые методы решения особых интегральных и интегро-дифференциальных уравнений // Итоги науки и техн. Сер. Мат. анал. 1980. Т. 18. С. 251-307.

11. Русак В. Н. Равномерная рациональная аппроксимация сингулярных интегралов // Изв. НАН Беларуси. Сер. физ.-мат. наук. 1993. № 2. С. 22–26.

12. Бокша А. Н. Приближение сингулярных интегралов рациональными функциями в равномерной метрике // Вестн. Бел. гос. ун-та. Сер. 1. Физ. Мат. Инф. 1997. № 3. С. 68-71.

13. Русак В. Н., Уазис А. Х. Рациональная аппроксимация сингулярных интегралов с дифференцируемой плотностью // Изв. БГПУ. Сер 3. Физ. Матем. Инф. Биол. Геогр. 2009. № 1(59). С. 8-11.

14. Поцейко, П. Г., Ровба Е. А. О приближениях одного сингулярного интеграла на отрезке рациональными интегральными операторами Фурье-Чебышева // Математический сборник. 2024. Т. 215. № 7. С. 96– 137.

15. Ровба Е. А. Об одном прямом методе в рациональной аппроксимации // Докл. АН БССР. 1979. Т. 23, № 11. С. 968-971.

16. Натансон И. П. О порядке приближения непрерывной 2𝜋-периодической функции при помощи ее интеграла Пуассона // Доклады АН СССР. 1950. Т. 72, № 1. С. 11-14.

17. Тиман А. Ф. Точная оценка остатка при приближении периодических дифференцируемых функций интегралами Пуассона // Доклады АН СССР. 1950. Т. 74, № 1. С. 17-20.

18. Жук В. В. О порядке приближения непрерывной 2𝜋-периодической функции при помощи средних Фейера и Пуассона ее ряда Фурье // Математические заметки. – 1968. – Т. 4, № 1. – С. 21–32.

19. Штарк Э. Л. Полное асимптотическое разложение для верхней грани уклонения функций из Lip 1 от сингулярного интеграла Абеля – Пуассона // Математические заметки. 1973. Т. 13, № 1. С. 21–28.

20. Русецкий Ю.И. О приближении непрерывных на отрезке функций суммами Абеля – Пуассона // Сибирский математический журнал. 1968. Т. 9, № 1. С. 136-144.

21. Жигалло Т. В. Приближение функций, удовлетворяющих условию Липшица на конечном отрезке вещественной оси, интегралами Пуассона – Чебышёва // Проблемы управления и информатики. 2018. Т. 3. С. 1-14.

22. Китбалян, А. А. Разложения по обобщенным тригонометрическим системам // Известия АН АССР. 1963. Т. XVI, № 6. С. 3-24.

23. Джрбашян М. М. К теории рядов Фурье по рациональным функциям // Известия АН

24. Армянской ССР. Сер. Математика. 1956. Т. 9, № 7. С. 1-27.

25. Поцейко, П. Г., Ровба Е. А. О рациональных суммах Абеля – Пуассона на отрезке и аппроксимациях функций Маркова // Журнал Белорусского государственного университета. Математика. Информатика. 2021. Т. 3. С. 6-24.

26. Лунгу К. Н. О наилучших приближениях рациональными функциями с фиксированным числом полюсов // Математический сборник. 1971. Т. 86(128), № 2(10). С. 314-324.

27. Лунгу К. Н. О наилучших приближениях рациональными функциями с фиксированным числом полюсов // Сибирский математический журнал. 1984. Т. 15, № 2. С. 151-160.

28. Русак В. Н. Рациональный функции как аппарат приближения // Минск: БГУ, 1979. 178 с.