Arithmetic properties of values of divergent in C series
https://doi.org/10.22405/2226-8383-2024-25-3-259-269
Abstract
The article describes the directions of research on the arithmetic properties of series values of the form
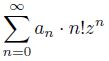
with coefficients 𝑎𝑛 satisfying certain conditions. Under these conditions, the considered series,
other than the polynomial, converges in the field C only at 𝑧 = 0. However, for almost all but a finite number of prime 𝑝 numbers, such a series converges in the fields Q𝑝. Therefore there are two ways of research. We can either consider the arithmetic properties of the result of some summation of this series, or consider the values of this series in the field Q𝑝. An example of the first approach is the series considered by Euler
as a result of the summation of which, with the substitution 𝑥 = 1, we obtain the remarkable
equality
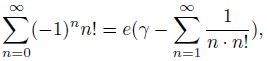
where 𝛾 – Euler’s constant.
Another direction of research uses the concept of global relation introduced by E. Bombieri.
Using the modified Siegel—Shidlovskii method, it is possible to obtain analogues of the main theorems of A.B. Shidlovskii for 𝐸− functions. The use of Hermite-Pade approximants made it possible to consider the values of generalized hypergeometric series not only with algebraic, but also with certain parameters transcendental in any field Q𝑝.
About the Author
Vladimir Grigorevich Chirskii
Lomonosov Moscow State University; Russian Presidential Academy of National Economy and Public Administration
Russian Federation
Russian Federation
doctor of physical and mathematical sciences
References
1. Shidlovskii, A. B. 1989, “Transcendental Numbers”, W.de Gruyter.-Berlin.-New York, 467 pp.
2. Hardy, G. H. 1949, “Divergent Series”, Clarendon Press.-London, 510 pp.
3. Ramis, J.P. 1993, “Series divergentes et theories asymptotiques”, Panoramas et Syntheses, no.21, Soc. Math. France. -Paris, 80 pp.
4. Ferguson, T. 2021, “Arithmetic properties of Э-functions”,J.Number Theoty, Vol, 229, pp.168– 178.
5. Fischler, S., Rivoal. T. 2016, “Arithmetic theory of E-operators”,J.d l’Ecole polytechnique-
6. Mathematiques, Vol, 3, pp.31–65.
7. Fischler, S., Rivoal, T. 2018, “Microsolutions of differential operators and values of arithmetic Gevrey series”, Michigan Math. J., Vol, 61, pp.239–254.
8. Rivoal, T. 2012, “On the arithmetic nature of the values of the Gamma function,Euler’s constant and Gompertz’s constant”,American J.of Math, Vol, 140,no.2. pp.317–348.
9. Andre, Y. 2003, “Arithmetic Gevrey series and transcendence. A survey”,J.Theor.Nombres Bordeaux, Vol, 15, pp.1–10.
10. Bertrand, D., Beukers, F. 1985, “Equations differentielles linearies et majorations de multiplicities ”,Annales scientifiques ENS, Vol, 18,no.1. pp.181–192.
11. Chirskii, V. G. 2019, “Product Formula, Global Relations and Polyadic Integers”, Russ. J. Math. Phys., Vol.26, no.3, pp.286–305.
12. Ernvall-Hytonen, A.-M., Matala-aho, T., Seppala, I. 2023, “ Euler’s factorial series, Hardy integral, and continued fractions”, J.Number Theory, Vol. 244, pp.224–250.
13. Chirskii, V. G. 2020, “ Arithmetic properties of generalized hypergeometric F- series”, Russ. J. Math. Phys., Vol.27, no.2, pp.175–184.
14. Chirskii, V. G.2014, “On the arithmetic properties of generalized hypergeometric series with irrational parameters .”, Izvestiya RAN. Ser. Math., Vol. 8, no.6, pp.193–210.
15. Chirskii, V. G.2021, “ Polyadic Liouvillean numbers .”, Chebyshevsky sbornik, Vol. 22, no.3, pp.245–255.
16. Chirskii, V. G. 2022, “ Arithmetic properties of the values of generalized hypergeometric series with polyadic transcendental parameter .”, Dokl. Math., Vol. 106, no.2, pp.386–397.
17. Chirskii, V. G. 2023, “Transcendence of p-adic values of generalized hypergeometric series with transcendental polyadic parameter .”, Dokl. Math., Vol. 107, no.2, pp.109–111.
18. Chirskii, V. G. 2023, “ Transcendence of certain 2-adic numbers .”, Chebyshevsky sbornik, Vol. 24, no.5, pp.194–200.
19. Yudenkova, E.Yu. 2021, “ Infinite linear and algebraic independence pf values of F-series at polyadic Liouvillean point .”, Chebyshevsky sbornik, Vol. 22, no.2, pp.334–346.
20. Matveev, V.Yu. 2019, “ Properties of elements of direct products of fields”, Chebyshevskii sbornik, Vol. 20, no.2, pp.383–390.
21. Krupitsin, E. S. 2019, “ Arithmetic properties of series of certain classes”, Chebyshevskii sbornik, Vol. 20, no.2, pp.374–382.
Review
For citations:
Chirskii V.G. Arithmetic properties of values of divergent in C series. Chebyshevskii Sbornik. 2024;25(3):259-269. (In Russ.) https://doi.org/10.22405/2226-8383-2024-25-3-259-269
Views:
65
Email this article 