Complex valued approach to the system of non-linear second order Boundary value problem and multivalued mapping via fixed point method
https://doi.org/10.22405/2226-8383-2023-24-3-212-227
Abstract
The main aim of this manuscript is to work on the application part of CVMS. In this work we have demonstrated some common fixed results and then we deal primarily with two parts of applications,
part(I) Complex valued version of existence and common solution for second order nonlinear boundary value problem using greens function,
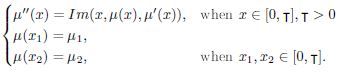
part(II) Application of fixed point results for multivalued mapping in setting of CVMS without using notion of continuity. Eventually several equivalent results and examples are presented to sustain our Main result.
References
1. S. Banach, 1922, “Sur les operations dans les ensembles abstraits et leurs application aux equations integrales”, Fund. Math., 3, pp. 133-–181.
2. L.B. Ciric, 1974, “A generalization of Banach’s contraction principle”, Proc. Amer.Math. Soc., 45, pp. 267-–273.
3. T. Dosenovic, D. Rakic, B. Caric, S. Radenovic, 2016, “Multivalued generalizations of fixed point results in fuzzy metric spaces”, Nonlinear Anal. Model. Control, 21, pp. 211-–222.
4. W.Shatanawi,V.Rajic, S.Radenovic, Al-Rawashdeh, 2012, “Mizoguchi–Takahashi-type theorem in tvs-cone metric spaces”, Fixed Point Theory Appl.
5. Azam, Fisher, Khan, 2011, “Common fixed point theorems in complex valued metric spaces”, Numer. Funct. Anal. Optim., 32, pp. 243-–253.
6. Rouzkard, Imdad, 2012, “Some common fixed point theorems on complex valued metric spaces”, Computers & Mathematics with Applications, 64, pp. 1866-–1874.
7. Ahmad, Klin-eam, Azam, 2013, “Common fixed points for multivalued mappings in complex valued metric spaces with applications”, Abstract and Applied Analysis, pp. 1–12.
8. Azam,Ahmad,Kumam, 2013, “Common fixed point theorems for multi-valued mappings in complex-valued metric spaces”, Journal of Inequalities and Applications, № 1, pp. 578.
9. Das, Gupta, 1975, “An extension of Banach contraction principle through rational expression”, Indian J. Pure Appl. Math., 6, pp. 1455-–1458.
10. Klin-eam, Suanoom, 2013, “Some common fixed-point theorems for generalized contractive mappings on complex-valued metric spaces”, Abstr. Appl. Anal.
11. Kutbi, Ahmad, Azam, Al-Rawashdeh, 2014, “Generalized common fixed point results via greatest lower bound property”, J. Appl. Math., pp. 1—11.
12. Sintunavarat, Kumam, 2012, “Generalized common fixed point theorems in complex valued metric spaces and applications”, J.Inequal.Appl., pp. 1—12.
13. Sintunavarat, B.Zada, Sarwar, 2017, “Common solution of Urysohn integral equations with the help of common fixed point results in complex valued metric spaces”, Rev. R. Acad.Exactas F ıs. Nat. Ser. A Mat. RACSAM, 111, pp. 531-–545.
14. Sintunavarat, Cho, Kumam, 2013, “Urysohn integral equations approach by common fixed points in complex valued metric spaces”, Adv. Difference Equ., pp. 1—14.
15. Jamshaid Ahmad, Klin Eam, Azam, 2013, “Common fixed point for Multivalued mappings in complex valued metric space with Application”, Abstract and Applied Analysis Vol., Article ID 854965, (2013), pp. 12.
16. Lakshmikantham, Mohapatra, 2003, “Theory of Fuzzy Differential Equations and Inclusions”, Taylor & Francis, Ltd., London.
17. Puri, Ralescu, 1986, “Fuzzy random variables”, J. Math. Anal. Appl., 114, pp. 409-–422.
18. Nashine, Vetro, Kumam, Kumam, 2014, “Fixed point theorems for fuzzy mappings and applications to ordinary fuzzy differential equations”, Adv. Difference Equ., pp. 1-–14.
Review
For citations:
Shinde S.R. Complex valued approach to the system of non-linear second order Boundary value problem and multivalued mapping via fixed point method. Chebyshevskii Sbornik. 2023;24(3):212-227. (In Russ.) https://doi.org/10.22405/2226-8383-2023-24-3-212-227






























