Generalized Estermann problem for non-integer powers with almost proportional summands
https://doi.org/10.22405/2226-8383-2025-26-5-184-202
Abstract
For 𝐻 ⩾ 𝑁1−^(1/2𝑐) (ln𝑁)^2, where L = ln𝑁 and 𝑐 is a fixed non-integer number satisfying
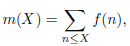
we obtain an asymptotic formula for the number of representations of a sufficiently large integer 𝑁 in the form
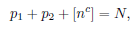
where 𝑝1, 𝑝2 are prime numbers, 𝑛 is a natural number, and
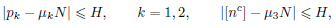
with 𝜇1, 𝜇2, 𝜇3 being fixed positive constants satisfying 𝜇1 + 𝜇2 + 𝜇3 = 1.
About the Authors
Firuz Zarulloevich Rakhmonov
A. Juraev Institute of Mathematics of the NAS of Tajikistan
Russian Federation
Russian Federation
candidate of physical and mathematical sciences
Parviz Zarulloevich Rakhmonov
Marex Group Plc
United Kingdom
United Kingdom
candidate of physical and mathematical sciences
References
1. Estermann, T., 1937, “Proof that every large integer is the sum of two primes and a square”, Proc. London Math. Soc., vol. 11, pp. 501–516.
2. Rakhmonov, Z. Kh., 2003, “Ternary Estermann problem with almost equal summands”, Matematicheskie Zametki (Mathematical Notes), vol. 74, Is. 4, pp. 564–572, (in Russian).
3. Rakhmonov, Z. Kh., 2014, “Cubic Estermann problem with almost equal summands”, Matematicheskie Zametki (Mathematical Notes), vol. 95, Is. 3, pp. 445–456, (in Russian).
4. Rakhmonov, F. Z., Rahimov, A. O., 2016, “On an additive problem with almost equal summands”, Research in Algebra, Number Theory, Functional Analysis and Related Topics, Saratov National Research State University, vol. 8, pp. 87–89, (in Russian).
5. Rakhmonov, F. Z., 2024, “Asymptotic formula in the generalization of ternary Estermann problem with almost proportional summands”, Chebyshevskii Sbornik, vol. 25, Is. 4(95), pp. 120–137, (in Russian).
6. Rakhmonov, Z. Kh., Rakhmonov, F. Z., 2024, “Asymptotic formula in Waring’s problem with almost proportional summands”, Chebyshevskii Sbornik, vol. 25, Is. 2(93), pp. 139–168, (in Russian).
7. Rakhmonov, Z. Kh., Rakhmonov, F. Z., 2024, “Asymptotic formula in Waring’s problem with almost proportional summands”, Doklady Natsional’noy Akademii Nauk Tadzhikistana, vol. 67, Is. 3-4, pp. 125–136, (in Russian).
8. Rakhmonov, Z. Kh., Rakhmonov, F. Z., 2023, “Waring’s problem with almost proportional summands”, Doklady Natsional’noy Akademii Nauk Tadzhikistana, vol. 66, Is. 9-10, pp. 481–488, (in Russian).
9. Rakhmonov, Z. Kh., Rakhmonov, F. Z., 2023, “Behaviour of short G. Weyl exponential sums on major arcs”, Doklady Natsional’noy Akademii Nauk Tadzhikistana, vol. 66, Is. 11-12, pp. 625–633, (in Russian).
10. Rakhmonov, Z. Kh., 2023, “Generalization of Waring’s problem for nine almost proportional cubes”, Chebyshevskii Sbornik, vol. 24, Is. 3, pp. 71–94, (in Russian).
11. Rakhmonov, P. Z., 2012, “Short trigonometric sums with a non-integer power of a natural number”, Vestnik Moskovskogo Universiteta. Seriya 1. Matematika. Mekhanika, Is. 6, pp. 51–55, (in Russian).
12. Rakhmonov, P. Z., 2012, “Short trigonometric sums with a non-integer power of a natural number”, Doklady Akademii Nauk Respubliki Tadzhikistan, vol. 55, Is. 3, pp. 185–191, (in Russian).
13. Rakhmonov, P. Z., 2014, “Short sums with non-integer powers of natural numbers”, Matematicheskie Zametki (Mathematical Notes), vol. 95, Is. 5, pp. 763–774, (in Russian).
14. Rakhmonov, P. Z., 2016, “Generalized ternary Estermann problem for non-integer powers with almost equal summands”, Matematicheskie Zametki (Mathematical Notes), vol. 100, Is. 3, pp. 410–420, (in Russian).
15. Rakhmonov, P. Z., 2015, “Generalized ternary Estermann problem for non-integer powers with almost equal summands”, Chebyshevskii Sbornik, vol. 16, Is. 1, pp. 248–253, (in Russian).
16. Rakhmonov, P. Z., 2013, “Generalized ternary Estermann problem for non-integer powers with almost equal summands”, Izvestiya Akademii Nauk Respubliki Tadzhikistan, No. 2(151), pp. 7–16, (in Russian).
17. Karatsuba, A. A., 1983, Basic analytic number theory, Moscow: Nauka, 2nd ed., (in Russian).
18. Zhan, T., 1992, “On the mean square of Dirichlet 𝐿-functions”, Acta Mathematica Sinica. New Series, vol. 8, No. 2, pp. 204–224.
19. Baker, R., Harman, G., 1996, “The difference between consecutive primes”, Proc. London Math. Soc., vol. 72, pp. 261–280.
20. Voronin, S. M., Karatsuba, A. A., 1994, Riemann zeta-function, Moscow: Fizmatlit, 376 pp., (in Russian).
21. Whittaker, E. T., Watson, G. N., 1963, A Course of Modern Analysis, Vol. 1: Fundamental Operations of Analysis, Moscow: Fizmatgiz, (in Russian).
Review
For citations:
Rakhmonov F.Z., Rakhmonov P.Z. Generalized Estermann problem for non-integer powers with almost proportional summands. Chebyshevskii Sbornik. 2025;26(5):184-202. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-5-184-202
Views:
30
JATS XML
Email this article 