Плотность нулей дзета-функции Римана в узких прямоугольниках критической полосы
https://doi.org/10.22405/2226-8383-2025-26-5-158-183
Аннотация
Для количества нулей дзета-функции Римана 𝜁(𝑠) в узких прямоугольниках критической полосы (Re 𝑠 ⩾ 𝛼 ⩾ 0,5 и 𝑇 < Im𝑠 ⩽ 𝑇 + 𝐻), при
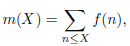
где (𝜅, 𝜆) — произвольная экспоненциальная пара, 𝜀 < 10^(−4) — любое фиксированное положительное число, 𝑇 ⩾ 𝑇0(𝜀) > 0, получена оценка вида
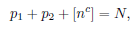
причём 𝑎 = 2, 4, 𝑐 = 172, если 1/2 ⩽ 𝛼 ⩽ 2/3 или 5/6 ⩽ 𝛼 ⩽ 1, и соответственно 𝑎 = 8
3 , 𝑐 = 50, если 2/3 < 𝛼 < 5/6 .
Об авторе
Зарулло Хусенович Рахмонов
Таджикский национальный университет
Таджикистан
Таджикистан
доктор физико-математических наук, академик НАН Таджикистана
Список литературы
1. Huxley M. N. On one difference between consecutive primes // Invent. Math. 1972. V. 15.P. 164 – 170.
2. Карацуба А. А. Распределение простых чисел // УМН. 1990. Т. 45. № 5(275). С. 81 – 140.
3. Гриценко С.А. О плотностной теореме // Математические заметки. 1992. Т. 51. № 6. С. 32 - 40.
4. Selberg A. On the zeros Riemann zeta function // Shr. Norske Vid. Akad. Oslo, 1942. V. 10. P. 1 – 59
5. Карацуба А. А. О нулях функции 𝜁(𝑠) на коротких промежутках критической прямой // Известия АН СССР. Серия математическая. 1984. Т. 48. № 3. С 569 – 584.
6. Карацуба А. А. О нулях функции 𝜁(𝑠) в окресности критической прямой // Известия АН СССР. Серия математическая 1985. Т. 49. № 2. С. 326 - 333.
7. Карацуба А. А. Дзета-функция Римана и ее нули // УМН. 1985. Т. 40. В. 5(245). С. 19 –70.
8. Воронин С. М., Карацуба А. А. Дзета–функция Римана // М.: Физматлит. 1994. 376 с.
9. Карацуба А. А. О нулях функции Дэвенпорта–Хейльбронна, лежащих на критической прямой // Известия АН СССР. Серия математическая. 1990. Т 54. № 2. С. 303 – 315.
10. Карацуба А. А. О нулях арифметических рядов Дирихле, не имеющих эйлерова произведения // Известия РАН. Серия математическая. 1993. Т 57, № 5. С. 3 – 14.
11. Карацуба А. А. Новый подход к проблеме нулей некоторых рядов Дирихле // Труды МИАН. 1994. Т. 207. С. 180 – 196.
12. Рахмонов З.Х. Нули дзета-функции Римана в коротких промежутках критической прямой // Чебышевский сборник. 2006. Т. 7. В. 1. С. 263 – 279.
13. Неъматова Г. Д, Хасанов З. Н. О нулях дзета–функции Римана в окрестности критической прямой // Доклады Академии наук Республики Таджикистан. Т. 44, № 3 – 4. С. 4 – 7.
14. Рахмонов З. Х., Аминов А. С. О нулях нечетного порядка функции Дэвенпорта-Хейльбронна в коротких промежутках критичекой прямой // Доклады Академии наук Республики Таджикистан. 2019. Т. 62, № 3-4. С. 133 – 138.
15. Рахмонов З. Х., Аминов А. С. О нулях нечетного порядка функции Дэвенпорта-Хейлбронна в коротких промежутках критической прямой // Современные проблемы математики и механики. Материалы международной конференции, посвященной 80-летию академика РАН В.А.Садовничего. 2019. Издательство «МАКС Пресс». ISBN: 978-5-317-06116-6. С. 522 – 525.
16. Рахмонов З. Х., Хайруллоев Ш. А., Аминов А. С. Нули функции Дэвенпорта-Хейлбронна в коротких промежутках критической прямой // Чебышевский сборник. 2019. Т. 20, В. 4. С. 271 – 293.
17. Heath Brown D.R. The fourth power moment of the Riemann zeta function // Proceedings of the London Mathematical Society. 1979. V. s3-38. Is. 3. P. 385 – 422,
18. Zhan Tao. On the mean square of Dirichlet 𝐿-functions // Acta Mathematica Sinica June. 1992. V. 8. Is. 2.P. 204 – 224
19. Рахмонов З.Х. Оценка плотности нулей дзета функции Римана // УМН. 1994. T. 49. Вып. 1. С. 161 – 162.
20. Bourgain J.,Watt N. Decoupling for perturbed cones and mean square of // arXiv:1505.04161v1 [math.NT]. 15 May 2015.
21. Рахмонов З. Х., Хайруллоев Ш. А. Расстояние между соседними нулями дзета-функции Римана, лежащими на критической прямой // Доклады Академии наук Республики Таджикистан. 2006. Т. 49. № 5. C. 393 – 400.
22. Рахмонов З. Х., Хайруллоев Ш. А. Соседние нули дзета-функции Римана, лежащие на критической прямой // Доклады Академии наук Республики Таджикистан. 2009. Т. 52, № 1. С. 5 – 15.
23. Рахмонов З. Х., Хайруллоев Ш. А. О нулях дзета-функции Римана на критической прямой // Вестник Таджикского национального университета. Спецвыпуск посвящён году образования и технических знаний. 2010. C. 35 – 41.
24. Марджанашвили К.К. Оценка одной арифметической суммы // Доклды АН СССР. 1939. Т. 22, № 22. С. 391 - 393.
25. Виноградов И. М. Метод тригонометрических сумм в теории чисел // Москва, Наука, 1971.
26. Архипов Г.И., Карацуба А.А., Чубариков В.Н. Теория кратных тригонометрических сумм // М.: Наука. 1987 г. 368 с.
27. Graham S. W., Kolesnik G. Van der Corput’s method of exponential sums // London Mathematical Society Lecture Note Series 126, Cambridge University Press, Cambridge, 1991. vi+120 pp.
28. Карацуба А. А. Основы аналитической теории чисел — М.:, Наука, 1983.
Рецензия
Для цитирования:
Рахмонов З.Х. Плотность нулей дзета-функции Римана в узких прямоугольниках критической полосы. Чебышевский сборник. 2025;26(5):158-183. https://doi.org/10.22405/2226-8383-2025-26-5-158-183
For citation:
Rakhmonov Z.Kh. Density of zeros of the Riemann zeta function in narrow rectangles of the critical strip. Chebyshevskii Sbornik. 2025;26(5):158-183. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-5-158-183
Просмотров:
34
JATS XML
Послать статью по эл. почте 