The sum of the products of multiplicative functions over numbers whose prime divisors lie in the specified intervals
https://doi.org/10.22405/2226-8383-2025-26-4-383-397
Abstract
Summation of multiplicative functions is found in almost half of the problems of analytical
number theory. The central place in the question of summing the values of multiplicative
functions is occupied by questions about the asymptotic behavior of sums of the form
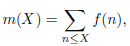
for 𝑋 → ∞, where 𝑓(𝑛) is a multiplicative function of a natural argument. This article is devoted to the study of summation of multiplicative functions over numbers whose prime divisors
lie in specified intervals. An asymptotic formula is obtained for the sums of the product of multiplicative functions whose prime divisors lie in specified intervals.
About the Author
Umidilla Charievich Chariyev
Tajik State Pedagogical University (Dushanbe) named after Sadriddin Ayni
Tajikistan
Tajikistan
candidate of physical and mathematical sciences
References
1. Buhshtab A. A. 1937, “Asymptotic estimation of a general number-theoretic function”, Matematicheskii Sbornik, Vol, 2, no. 44:6, pp. 1239–1246.
2. Buhshtab A. A. 1949, “On numbers in arithmetic progression with small prime factors”, Doklady Akademii Nauk SSSR, Vol, 67, no. 1, pp. 5–8.
3. Buhshtab A. A. 1951, “On asymptotic estimation of numbers in arithmetic progression not divisible by relatively small primes”, Matematicheskii Sbornik, Vol, 28, no. 44:16, pp. 165–184.
4. Vinogradov I. M. 1956, “On numbers with small prime divisors”, Doklady Akademii Nauk SSSR, Vol, 109, no. 4, pp. 683–686.
5. Linnik Yu. V. 1942, “Remarks on the least quadratic non-residue”, Doklady Akademii Nauk SSSR, Vol, 36, no. 4–5, pp. 131–132.
6. Levin B. V., Fainleib A. S. 1963, “On a class of number theory problems reducible to differential equations with retarded argument”, Nauchnye Trudy Tashkentskogo Universiteta, Vol, 228, pp. 56–69.
7. de Bruijn N. G. 1951, “The asymptotic behaviour of a function occurring in the theory of primes”, Journal of the Indian Mathematical Society, Vol, 15, pp. 25–32.
8. Rankin R. A. 1938, “The difference between consecutive primes”, Journal of the London Mathematical Society, Vol, 13, pp. 242–247.
9. Levin B. V., Fainleib A. S. 1985, “Application of some integral equations to number theory problems”, Uspekhi Matematicheskikh Nauk, Vol, 22, no. 3(135), pp. 119–199.
10. Friedlander J. B. 1976, “Integers free from large and small primes”, Proceedings of the London Mathematical Society, Vol, 33, no. 3, pp. 565–575.
11. Chariyev U. 1979, “Asymptotic behavior of solutions of some differential-difference equations”, Doklady Akademii Nauk Tadzhikskoi SSR, Vol, 22, no. 8, pp. 463–465.
Review
For citations:
Chariyev U.Ch. The sum of the products of multiplicative functions over numbers whose prime divisors lie in the specified intervals. Chebyshevskii Sbornik. 2025;26(4):383-397. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-4-383-397
Views:
4
Email this article 