Arithmetic properties of values of divergent in C series. Conjectures
https://doi.org/10.22405/2226-8383-2025-26-3-300-306
Abstract
The article describes the directions of research on the arithmetic properties of series values of the form
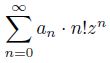
with coefficients 𝑎𝑛 satisfying certain conditions. Under these conditions, the considered series, other than the polynomial, converges in the field C only at 𝑧 = 0. However, for almost all but a finite number of primes, such a series converges in the fields Q𝑝. Therefore there are two ways of research. We can either consider the arithmetic properties of the result of some summation of this series, or consider the values of this series in the field Q𝑝. The paper formulates conjectures, related to the values of the considered series.
About the Author
Vladimir Grigorevich Chirskii
Lomonosov Moscow State University; Russian Presidential Academy of National Economy and Public Administration
Russian Federation
Russian Federation
doctor of physical and mathematical sciences
References
1. Chirskii V. G.2024.“ Arithmetic properties ov values of divergent in 𝐶 series .”, Chebyshevskii sbornik, Vol. 25, no.3, pp.259-269.
2. Shidlovskii, A. B.1989.“ Transcendental Numbers”, W.de Gruyter.-Berlin.-New York.467pp.
3. Hardy G.H.1949.“ Divergent Series”, Clarendon Press.-London.510pp.
4. Ramis, J.P.1993.“ Series divergentes et theories asymptotiques”, Panoramas et Syntheses, no.21, Soc. Math. France. -Paris. 80pp.
5. Ferguson. T.2021.“Arithmetic properties of Э-functions”,J.Number Theoty, Vol, 229, pp.168-178.
6. Fischler. S.;Rivoal. T.2016.“Arithmetic theory of E-operators”,J.d l’Ecole polytechnique-Mathematiques, Vol, 3, pp.31-65.
7. Fischler.S.;Rivoal.T.2018.“Microsolutions of differential operators and values of arithmetic Gevrey series”,Michigan Math. J., Vol, 61, pp.239-254.
8. Rivoal.T.2012.“On the arithmetic nature of the values of the Gamma function,Euler’s constant and Gompertz’s constant”,American J.of Math, Vol, 140,no.2. pp.317-348.
9. Fischler. S.;Rivoal. T.2023. “Relations between values of arithmetic Gevrey series, and applications to values of the Gamma function”,( arXiv:2301.13518v1[math.NT])
10. Andre.Y.2003.“Arithmetic Gevrey series and transcendence. A survey”,J. Theor. Nombres Bordeaux, Vol, 15, pp.1-10.
11. Bertrand.D.;Beukers.F.1985.“Equations differentielles linearies et majorations de multiplicities ”,Annales scientifiques ENS, Vol, 18,no.1. pp.181-192.
12. Chirskii V. G. 2019. “Product Formula, Global Relations and Polyadic Integers”, Russ. J. Math. Phys., Vol.26, no.3, pp.286-305.
13. Chirskii V. G.2020. “ Arithmetic properties of generalized hypergeometric F- series”, Russ. J. Math. Phys., Vol.27, no.2, pp.175-184.
14. Ernvall-Hytonen A.-M.;Matala-aho T.;Seppala I. 2023. “ Euler’s factorial series, Hardy integral, and continued fractions”, J. Number Theory, Vol. 244, pp.224-250.
Review
For citations:
Chirskii V.G. Arithmetic properties of values of divergent in C series. Conjectures. Chebyshevskii Sbornik. 2025;26(3):300-306. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-300-306
Views:
23
Email this article 