Albertson index and Sigma index in trees given by degree sequences
https://doi.org/10.22405/2226-8383-2025-26-3-274-283
Abstract
In our paper we study Albertson Index and Sigma index in Trees Given by Degree Sequences and introduced the irregularity of Albertson Index and Sigma index for sequences of degree(2,3,4), We supported this with a set of illustrative examples of obtaining the general relationship as:
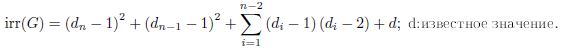
About the Authors
Jasem Hamoud
Moscow Institute of Physics and Technology (National Research University)
Russian Federation
Russian Federation
postgraduate student
Duaa Abdullah
Moscow Institute of Physics and Technology (National Research University)
Russian Federation
Russian Federation
postgraduate student
References
1. Lina, Z., Zhoub, T. and Miaob, L. 2024, “The general Albertson irregularity index of graphs”, AIMS Mathematics, Vol, 7, Iss. 1, pp. 267–282. Available at: https://doi.org/10.3934/math.2022002
2. Haynes, T.W., Hedetniemi, S.T. Slater, P.J. 1998, Fundamentals of Domination in Graphs. New York: Marcel Dekker, Inc.
3. Dorjsembe, S., Buyantogtoh, L., Gutman, I., Khoroldagva, B., Reti, T. 2023, “Irregularity of graphs”, Journal of Communications in Mathematical and in Computer Chemistry, volume 89, pp. 371–388. Available at: https://doi.org/10.46793/match.89-2.371D
4. Ali, A., Dimitrov, D., Reti, T., Albalahi, A.M., Hamza, A.E. 2025, “Bounds and optimal results for the total irregularity measure”, arXiv [Preprint]. Available at: https://doi.org/10.48550/arXiv.2501.01538
5. Gutman, I., Kulli, V.R. and Redzepovic, I. 2023, “Irregularity Sombor index”, Bulletin of the Academy of Serbe Sciences and Arts (Class of Mathematical and Natural Sciences), volume 156, pp. 31–37.
6. Galavand, A., Ashrafi, A., Dimitrov, D. 2023, “On the irregularity of graphs based on the arithmetic-geometric mean inequality”, Mathematical Inequalities & Applications, volume 26, issue 1, pp. 151–160. Available at: https://doi.org/10.7153/mia-2023-26-12
7. Abdo, H., Dimitrov, D., Gutman, I. 2019, “Graph irregularity and its measures”, Applied Mathematics and Computation, volume 357, pp. 317–324. Available at: https://doi.org/10.1016/j.amc.2019.04.013
8. Mandal, Y.C. Prvanovic, M. 2022, “Inverse problem for Albertson irregularity index”, Journal of Algebraic Engineering Mathematics, volume 12, issue 3, pp. 1–10.
9. Gutman, I., Russich, B., Trinaistich, N., Wilcox, K. F. 1975, “Graph theory and molecular orbitals. XII. Acyclic polyenes”, Journal of Chemical Physics, volume 62, issue 9, pp. 3399–3405.
10. I. Gutman., M. Togan., Yurtash A. N., Dzhevik A. S., Dzhangul I. N. 2016, “Inverse problem for sigma index”, MATCH Communications in Mathematical and in Computer Chemistry, volume 79, issue 2, pp. 491–508.
11. Gutman, I. Trinajsti´c, N., 1972, “Graph theory and molecular orbitals. Total 𝜋-electron energy of alternant hydrocarbons”, Chemical Physics Letters, volume 17, issue 4, pp. 535–538.
12. Galavand A., Gutman I., Tavakoli M., Bessi S., Gonzalves D., Reinald A. 2023, “Irregularity measure of graphs”, Journal of Mathematics, volume 2023. Available at: https://doi.org/10.1155/2023/4891183
13. Xu, K., 2023, “Trees with the seven smallest and eight greatest Harary indices”, Discrete Applied Mathematics, volume 160, issue 3, pp. 321–331. Available at: https://doi.org/10.1016/j.dam.2011.08.014
14. Nikoli´c S., Kovacevich G., Milicevich A., Trinaistich N. 2003, “The Zagreb indices 30 years after”, Croatica Chemica Acta, volume 76, issue 2, pp. 113–124.
15. Albertson, M.O., 1997, “The irregularity of a graph”, Ars Combinatoria, volume 46, pp. 219–226.
16. Gutman, I., Hansen, P. and M´elot, H., 2005, “Variable neighborhood search for extremal graphs.
17. Comparison of irregularity indices for chemical trees”, Journal of Chemical Information and Modeling, volume 45, issue 2, pp. 222–230.
18. Abdo, H., Brandt, S. and Dimitrov, D., 2014, “The total irregularity of a graph”, Discrete Mathematics & Theoretical Computer Science, volume 16, issue Graph Theory, pp. 201–206.
Review
For citations:
Hamoud J., Abdullah D. Albertson index and Sigma index in trees given by degree sequences. Chebyshevskii Sbornik. 2025;26(3):274-283. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-274-283
Views:
44
Email this article 