Sum of short exponential sums with prime numbers
https://doi.org/10.22405/2226-8383-2025-26-3-235-246
Abstract
For sufficiently large integers 𝐾, 𝑥, 𝑦, 𝑞, subject to 𝐾 ⩽ 𝑦 < 𝑥, 𝑛 — fixed natural number, 𝛼 — real, |𝛼 − 𝑎/𝑞|⩽ 1/𝑞^2 , (𝑎, 𝑞) = 1, 𝑞 ⩾ 1, an estimate of the form
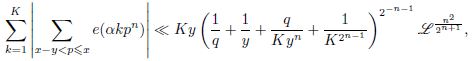
which is a strengthening and generalization of I. M. Vinogradov’s theorem on the distribution of fractional parts of {𝛼𝑝}.
About the Author
Firuz Zarulloevich Rakhmonov
A. Juraev Institute of Mathematics of the National Academy of Sciences of Tajikistan
Russian Federation
Russian Federation
candidate of physical and mathematical sciences
References
1. Vinogradov, I. M., 1952, Izbrannye trudy. (Russian) [Selected works.], Izdat. Akad. Nauk SSSR, Moscow.
2. Vinogradov, I. M., & Karatsuba, A. A., 1986, “The method of trigonometric sums in number theory”, Proc. Steklov Inst. Math., vol. 168, pp. 3-30.
3. Rakhmonov, Z. Kh., 1994, “Theorem on the mean value of 𝜓(𝑥, 𝜒) and its applications”, Russian Academy of Sciences. Izvestiya Mathematics, vol. 43, Is. 1, pp. 49 – 64.
4. Rahmonov, F. Z., 2011, “Estimate of quadratic trigonometric sums with prime numbers”, Vestnik Moskov. Univ. Ser. 1. Mat. Mekh., no. 3, pp. 56 – 60.
5. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2014, “Sum of short exponential sums over prime numbers”, Doklady Mathematics, vol. 90, No 3, pp. 699–700.
6. Rakhmonov, Z. Kh., & Rakhmonov, F. Z., Ismatov S. N., 2013, “Estimate of sums of short exponential sums over prime numbers”, Doklady Akademii nauk Respubliki Tadzhikistan, vol. 56, no 12, pp. 937-945, (in Russian).
7. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2024, “Asymptotic formula in the Waring’s problem with almost proportional summands”, Chebyshevskii Sbornik, vol. 25, Is. 2, pp. 138–168, (in Russian).
8. Rakhmonov, F. Z., 2024, “Asymptotic formula in generalization of ternary Esterman problem with almost proportional summands”, Chebyshevskii Sbornik, vol. 25, Is. 4, pp. 120–137, (in Russian).
9. Rakhmonov, F. Z., 2024, “Estimate of short G.Weyl exponential sums on minor arcs”, Doklady Natsional’noy akademii nauk Tadzhikistana, vol. 67, Is 5-6, pp. 238-242.
10. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2023, “Waring’s problem with almost proportional summands”, Doklady Natsional’noy akademii nauk Tadzhikistana, vol 66, Is 9-10, pp. 481-488.
11. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2024, “Asymptotic formula in the Waring’s problem with almost proportional summands”, Doklady Natsional’noy akademii nauk Tadzhikistana, vol 67, Is 3-4, pp. 125-136.
12. Vaughan R. C., 1981. The Hardy-Littlewood method, Cambridge Tracts in Mathematics, vol. 80, Cambridge University Press, Cambridge, 172 p.
13. Rakhmonov, F. Z., 2011, “Estimation of trigonometric sums with prime numbers”, Chebyshevskii Sbornik, vol. 12, Is. 1, pp. 158–171, (in Russian).
14. Rakhmonov, F. Z., 2011, “Estimate of quadratic trigonometric sums with prime numbers”, Vestnik Moskovskogo Universiteta. Seriya 1. Matematika. Mekhanika, Is. 3, pp. 56–60.
15. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2017, “Short Cubic Exponential Sums over Primes”, Proceedings of the Steklov Institute of Mathematics, vol. 296, pp. 211–233.
16. Rakhmonov, Z. Kh.,& Rakhmonov, F. Z., 2019, “Short cubic exponential sums with M¨obius function”, Chebyshevskii Sbornik, vol. 20, Is. 4, pp. 281–305, (in Russian).
17. Arkhipov G. I., Chubarikov V. N., 1994, “Three theorems in the analysis of trigonometric sums”, Doklady Mathematics, vol. 49, No 2, pp. 326–327.
18. Arkhipov G. I.,& Sadovnichii V. A., Chubarikov V. N., 1999, Lectures on mathematical analysis.: Textbook for universities and pedagogical universities, / Ed. V. A. Sadovnichii – Moscow: Higher School — 695 p.
19. Mardjhanashvili, K. K., 1939, “An estimate for an arithmetic sum”, Doklady Akad. Nauk SSSR, vol. 22, no 7, pp. 391–393.
20. Karatsuba A. A., 1993, Basic analytic number theory, Springer-Verlag, Berlin, xiv+222 pp.
21. Heath-Brown D. R., 1988, “The number of primes in a short interval”, Journal f¨ur die reine und angewandte Mathematik, vol. 389, pp 22-63.
Review
For citations:
Rakhmonov F.Z. Sum of short exponential sums with prime numbers. Chebyshevskii Sbornik. 2025;26(3):235-246. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-235-246
Views:
35
Email this article 