Uniform distribution in the unit cube of weighted nodes of the quadrature formula
https://doi.org/10.22405/2226-8383-2025-26-3-185-219
Abstract
The paper defines a uniform distribution in a unit 𝑠-dimensional cube of a sequence of nested generalized parallelepiped grids of type II with a weight function. In addition, a definition of a uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of 𝑀𝑛 grids with a weight
function is given.
A proof is given of an analogue of the generalized G. Weyl criterion on necessary and sufficient conditions for a uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of 𝑀𝑛 grids with weights.
Since the definition of the uniform distribution of a sequence of nested generalized parallelepiped grids of type II with a weight function differs from the definition of the uniform distribution of a sequence of grids 𝑀𝑛 with a weight function, the paper proves the second analogue of the Weyl criterion on the necessary and sufficient conditions for the uniform distribution in a unit 𝑠-dimensional cube 𝐺𝑠 of a sequence of nested generalized parallelepiped grids of type II.
The following theorem is proved:
Theorem 2. Let the Fourier series of 𝑓(⃗𝑥) converge absolutely, 𝐶(⃗𝑚) be its Fourier coefficients and 𝑆𝑀,⃗𝜌(⃗𝑚) be the trigonometric sums of the weighted grid, then the following equality holds
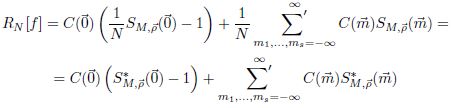
and as 𝑁 → ∞ the error 𝑅𝑁[𝑓] will tend to zero if and only if the weighted nodes of the quadrature formula are uniformly distributed in the unit 𝑠–dimensional cube.
About the Authors
Elena Mikhailovna Rarova
Tula State Lev Tolstoy Pedagogical University
Russian Federation
Russian Federation
Nikolai Nikolaevich Dobrovol’skii
Tula State Lev Tolstoy Pedagogical University; Lomonosov Moscow State University
Russian Federation
Russian Federation
doctor of physical and mathematical sciences
Irina Yuryevna Rebrova
Tula State Lev Tolstoy Pedagogical University
Russian Federation
Russian Federation
candidate of physical and mathematical sciences
Irina Nikolaevna Balaba
Tula State Lev Tolstoy Pedagogical University
Russian Federation
Russian Federation
doctor of physical and mathematical sciences, professor
References
1. Babenko, K.I. 1986, Osnovy chislennogo analiza [Fundamentals of Numerical Analysis], Nauka, Moscow, Russia.
2. Bakhvalov, N.S. 1959, “On approximate computation of multiple integrals”, Vestnik Moskovskogo universiteta, no. 4, pp. 3–18.
3. Bocharova (Dobrovol’skaya), L.P. 2007, “Algorithms for finding the optimal coefficients”, Chebyshevskij sbornik, vol. 8, no. 1(21), pp. 4–109.
4. Gertsog, A.S., Rebrov, E.D., Trikolich, E.V. 2009, “On K.K. Frolov’s method in the theory of quadrature formulas”, Chebyshevskii sbornik, vol. 10, no. 2(30), pp. 10–54.
5. Gertsog, A.S. 2011, “Numerical computation of quadruple integrals by Frolov’s method using algebraic nets of biquadratic Dirichlet field Q(√2+√3)”, Proceedings of Tula State University. Natural Sciences, no. 3, pp. 22–30.
6. Gertsog, A.S. 2011, “Parametrization of four-dimensional net of biquadratic Dirichlet field”, Scientific Bulletin of Belgorod State University. Series: Mathematics. Physics, no. 23(188), no. 5, pp. 41–53.
7. Gertsog, A.S. 2011, “TMK SICS: Biquadratic fields and quadrature formulas”, in: Multiscale Modeling of Structures and Nanotechnologies, Tula, pp. 242–247.
8. Dobrovol’skaya, L.P., Dobrovol’skii, N.M., Dobrovol’skii, N.N., Ogorodnichuk, N.K., Rebrov, E.D. and Rebrova, I.YU. 2012, “Some questions of the number-theoretic method in the approximate analysis”, Proceedings of the X International Conference "Algebra and Number Theory: Modern Problems and Applications"Scientific Notes of Orel State University, no. 6,
9. part 2, pp. 90–98.
10. Dobrovol’skaya, L.P., Dobrovol’skii, M.N., Dobrovol’skii, N.M. and Dobrovol’skii, N.N. 2012, “The hyperbolic Zeta function of grids and lattices, and calculation of optimal coefficients”, Chebyshevskii sbornik, vol. 13, no. 4(44), pp. 4–107.
11. Dobrovol’skaya, L.P., Dobrovol’skii, N.M. and Simonov, A.S. 2008, “On the error of approximate integration over modified grids”, Chebyshevskii sbornik, vol. 9, no. 1(25), pp. 185–223.
12. Dobrovol’skii, N.M. 1984, “Evaluation of generalized variance parallelepipedal grids”, Dep. v VINITI, no. 6089–84.
13. Dobrovol’skii, N.M. 1984, “The hyperbolic Zeta function of lattices”, Dep. v VINITI, no. 6090– 84.
14. Dobrovol’skii, N.M. 1984, “On quadrature formulas in classes 𝐸𝛼 𝑠 (𝑐) and 𝐻𝛼 𝑠 (𝑐)”, Dep. v VINITI, no. 6091–84.
15. Dobrovol’skii, N.M. 1984, “Number-theoretic meshes and their applications”, Ph.D. Thesis, Tula, Russia.
16. Dobrovol’skii, N.M. 1985, “Number-theoretic meshes and their applications”, Abstract of Ph.D. dissertation, Moscow State Pedagogical University, Moscow, Russia.
17. Dobrovol’skii, N.M. 1985, “Number-theoretic meshes and their applications”, Theory of Numbers and Its Applications: Abstracts of the All-Union Conference, Tbilisi, USSR, pp. 67–70.
18. Dobrovol’skii, N.N. 2018, “On two asymptotic formulas in the theory of hyperbolic Zeta function of lattices”, Chebyshevskii sbornik, vol. 19, no. 1, pp. 109–134.
19. Korobov, N.M. 1959, “The evaluation of multiple integrals by method of optimal coefficients”, Vestnik Moskovskogo universiteta, no. 4, pp. 19–25.
20. Korobov, N.M. 1959, “On approximate computation of multiple integrals”, Doklady Akademii nauk SSSR, vol. 124, no. 6, pp. 1207–1210.
21. Korobov, N.M. 1960, “Properties and calculation of optimal coefficients”, Doklady Akademii nauk SSSR, vol. 132, no. 5, pp. 1009–1012.
22. Korobov, N.M. 1963, Teoreticiko-chislovye metody v priblizhennom analize [Number-Theoretic Methods in Approximate Analysis], Fizmatgiz, Moscow, Russia.
23. Korobov, N.M. 2004, Teoreticiko-chislovye metody v priblizhennom analize [Number-Theoretic Methods in Approximate Analysis], 2nd ed., MTSNMO, Moscow, Russia.
24. Kurosh, A.G. 1963, Kurs vysshei algebry [Course of Higher Algebra], Fizmatgiz, Moscow, Russia.
25. Lokutsievskij, O.V. and Gavrikov, M.B. 1995, Nachala chislennogo analiza [Fundamentals of Numerical Analysis], TOO "Yanus Moscow, Russia.
26. Ogorodnichuk, N.K. and Rebrov, E.D. 2010, “On the algorithm of numerical integration with stopping rule”, in: Algebra and Number Theory: Modern Problems and Applications, Tula, pp. 153–158.
27. Ogorodnichuk, N.K. and Rebrov, E.D. 2011, “TMK SICS: Integration algorithms with stopping rule”, in: Multiscale Modeling of Structures and Nanotechnologies, Tula, pp. 153–158.
28. Rarova, E.M. 2014, “Decomposition of the trigonometric sum of a grid with weights in a series by lattice points”, Proceedings of Tula State University. Natural Sciences, vol. 1, part 1, pp. 37–49.
29. Rarova, E.M. 2014, “Trigonometric grid sums with weights for integer lattice”, Proceedings of Tula State University. Natural Sciences, no. 3, pp. 34–39.
30. Rarova, E.M. 2015, “Trigonometric sums of algebraic nets”, in: Algebra, Number Theory and Discrete Geometry: Modern Problems and Applications, Tula, pp. 356–359.
31. Rarova, E.M. 2018, “Weighted number of points of algebraic net”, Chebyshevskii sbornik, vol. 19, no. 1, pp. 200–219.
32. Rarova, E.M. 2019, “Trigonometric sums of nets of algebraic lattices”, Chebyshevskii sbornik, vol. 20, no. 2, pp. 399–405.
33. Rarova, E.M., Dobrovol’skii, N.N. and Rebrova, I.Yu. 2020, “Asymptotic estimation for trigonometric sums of algebraic grids”, Chebyshevskii sbornik, vol. 21, no. 3, pp. 232–240.
34. Rarova, E.M., Dobrovol’skii, N.N., Rebrova, I.Yu. and Dobrovol’skii, N.M. 2021, “Trigonometric sums of grids of algebraic lattices with infinitely differentiable weights”, Chebyshevskii sbornik, vol. 22, no. 3, pp. 166–178.
35. Rebrov, E.D. 2009, “Dobrovolskaya’s algorithm and numerical integration with stopping rule”, Chebyshevskii sbornik, vol. 10, no. 1(29), pp. 65–77.
36. Rebrov, E.D. 2012, “Quadrature formulas with modified algebraic grids”, Chebyshevskii sbornik, vol. 13, no. 3(43), pp. 53–90.
37. Rebrova, I.Yu., Dobrovolskii, N.M., Dobrovolskii, N.N., Balaba, I.N., Yesayan, A.R. and Basalov, Yu.A. 2016, Number-Theoretic Method in Approximate Analysis and Its Implementation in TMK SICS: Monograph, Part I, Tula State Pedagogical University, Tula, Russia.
38. Frolov, K.K. 1976, “Upper bounds on the error of quadrature formulas on classes of functions”, Doklady Akademii nauk SSSR, vol. 231, no. 4, pp. 818–821.
39. Frolov, K.K. 1979, “Quadrature formulas on classes of functions”, Ph.D. Thesis, Computing Center of Academy of Sciences of USSR, Moscow, USSR.
40. Dobrovolskiy, N.M., Dobrovolskaya, L.P., Dobrovolskiy, N.N., Ogorodnichuk, N.K. and Rebrov, E.D. 2012, “Algorithms for computing optimal coefficients”, Book of Abstracts of the International Scientific Conference "Computer Algebra and Information Technology", Odessa, pp. 22–24.
Review
For citations:
Rarova E.M., Dobrovol’skii N.N., Rebrova I.Yu., Balaba I.N. Uniform distribution in the unit cube of weighted nodes of the quadrature formula. Chebyshevskii Sbornik. 2025;26(3):185-219. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-3-185-219
Views:
23
Email this article 