On the diameters of some classes of analytic functions in Bergman space
https://doi.org/10.22405/2226-8383-2025-26-1-116-130
Abstract
The paper studies extremal problems related to the best polynomial approximation of functions that are analytic in the unit disk and belong to the Bergman space 𝐵2 with a finite norm
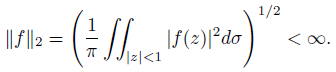
Let
An exact theorem is proved between the value of the best approximation 𝐸𝑛−1(𝑓)2 and the value of the modulus of continuity of the mth order sin(𝜋𝑡/ℎ) (0 < ℎ ⩽ 𝜋/𝑛) of functions 𝜔𝑚(𝑓(𝑟), 𝑡)2 averaged with the weight 𝑓 ∈ 𝐵(𝑟)2 . The connection between the proven theorem and the behavior of exact constants in the Jackson-Stechkin inequality for moduli of continuity 𝜔𝑚(𝑓(𝑟), 𝑡)2 is clarified. For the class of functions 𝑊(𝑟) 𝑚 (Φ)2, given a given monotonically increasing moharant Φ, satisfying some restrictions, the exact values of various 𝑛-widths in 𝐵2 space are calculated.
About the Authors
Mirgand Shabozovich Shabozov
Tajik National University
Tajikistan
Tajikistan
doctor of physical and mathematical sciences, professor
Dilshod Kamaridinovich Tukhliyev
Khujand State University named after academician Bobojon Gafurov
Tajikistan
Tajikistan
candidate of physical and mathematical sciences
References
1. Smirnov, V. I., Lebedev, N. А. 1964, “Constructive theory of functions of complex analysis“. —Moscow; Leningrad: Nauka, 440 p.
2. Babenko, K. I. 1958, “On the best approximations of one class of analytic functions“, Izvestiya Academy Nauk SSSR, vol. 22, no. 5, pp. 631-640.
3. Tikhomirov, V. М. 1960, “Diameters of sets in function spaces and the theory of best approximations“, UМN, vol. 15, no. 3, pp. 81-120.
4. Taikov, L. V. 1963, “On the best linear methods for approximating functions of the classes B𝑟 and 𝐻𝑟“, UMN, vol. 18, no. 4, pp. 183-189.
5. Taikov, L. V. 1967, “Best approximation in the mean of certain classes of analytic functions“, Math. Notes, vol. 1, no. 2, pp. 155-162.
6. Sheik, J. T. 1966, “Polynomial Approximation of functions analytic in a disc“, Proc. Amer. Math. Soc., vol. 17, no. 6, pp. 1238-1243.
7. Belyi, V. I., Dvejrin, М. Z. 1971, “On the best linear approximation methods on classes of functions defined by allied kernels. Metric questions in the theory of functions and mappings“, Publ, “Naukovo dumka“, vol. 2, pp. 37-54.
8. Dvejrin, М. Z., Chebanenko, I. V. 1983, “On polynomial approximation in Banach spaces of analytic functions“, Map theory and function approximation. Naukovo dumka. Kyiv., pp. 63-73.
9. Farkov, Yu. А. 1990, “Diameters of the Hardy and Bergman classes in a ball of C𝑛“, UMN, vol. 45, no. 3, pp. 197-198.
10. Vakarchuk, S. B. 1995, “Best linear methods of approximation and widths of classes of analytic functions in a disk“, Math. Notes, vol. 57, no. 1, pp. 30-39.
11. Vakarchuk, S. B. 1999, “On the best linear approximation methods and the widths of certain classes of analytic functions“, Math. Notes, vol. 65, no. 2, pp. 186-193.
12. Vakarchuk, S. B., Zabutnaya, V. I. 2009, “Best Linear Approximation Methods for Functions of Taikov Classes in the Hardy spaces 𝐻𝑞,𝜌 𝑞 ⩾ 1, 0 < 𝜌 ⩽ 1“, Math. Notes, vol. 85, no. 3, pp. 323-329.
13. Vakarchuk, S. B., Shabozov, М. Sh. 2010, “The widths of classes of analytic functions in a disc“, Sb. Math., vol. 201, no. 8, pp. 3-22.
14. Shabozov, М. Sh., Langarshoev, М. R. 2019, “Best linear approximation methods for some classes of analytic functions on the unit disk“, Siberian Math. J., vol. 60, no. 6, pp. 1414-1423.
15. Shabozov, М. Sh., Yusupov, G. А., Zargarov, J. J. 2021, “On the best simultaneous polynomial approximation of functions and their derivatives in Hardy spaces“, Trudy IMM Uro RAN., vol. 27, no. 4, pp. 239-254.
16. Shalaev V. V. 1991, “On the cross-sections in 𝐿2 of classes of differentiable functions defined by higher-order continuity modules“, Ukrainian Math. J., vol. 43, no. 1, pp. 125-129.
17. Korneychuk, N.P. 1976, “Extremal problems approximation theory“, Moscow.: Nauka. 320 p.
18. Shabozov, М. Sh. 2023, “On the Best Simultaneous Approximation in the Bergman Space 𝐵2“, Math. Notes, vol. 114, no. 3, pp. 435-446.
19. Shabozov, М. Sh., Saidusajnov, М. S. 2018, “Upper Bounds for the Approximation of Certain Classes of Functions of a Complex Variable by Fourier Series in the Space 𝐿2 and 𝑛-Widths“, Math. Notes, vol. 103, no. 4, pp. 617-631.
20. Shabozov, М. Sh., Khuromonov, Kh. M. 2020, “On the best approximation in the mean of functions of a complex variable by Fourier series in the Bergman space“, Russian Math. (Iz. VUZ)., no. 2, pp. 74-92.
21. Khuromonov, Kh. M. 2023, “On the best joint approximation of functions in Bergman space 𝐵2“, Russian Math. (Iz. VUZ)., no. 5, pp. 71-81.
22. Pinkus, А. 1985, “𝑛-Widths by Approximation Theory“, —Berlin: Springer. 312 p.
23. Tikhomirov, V. M. 1976, “Some questions of approximation theory“, —Moscow State University 325 p.
24. Ainulloev, N. 1984, “The value of the diameters of some classes of differentiable functions in 𝐿2“, Doklady АN ТаjSSR., vol. 29, no. 8, pp. 415-418.
Review
For citations:
Shabozov M.Sh., Tukhliyev D.K. On the diameters of some classes of analytic functions in Bergman space. Chebyshevskii Sbornik. 2025;26(1):116-130. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-1-116-130
Views:
24
Email this article 