О поперечниках некоторых классов аналитических функций в пространстве Бергмана

Аннотация

В работе изучаются экстремальные задачи, связанные с наилучшим полиномиальным приближением аналитических в единичном круге функций, принадлежащих пространству Бергмана 𝐵2, с конечной нормой

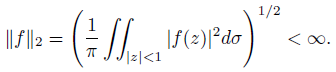
Пусть

Доказана точная теорема между величиною наилучшего приближения 𝐸𝑛−1(𝑓)2 и усредённым с весом sin(𝜋𝑡/ℎ) (0 < ℎ ⩽ 𝜋/𝑛) значением модуля непрерывности 𝑚-го порядка 𝜔𝑚(𝑓(𝑟), 𝑡)2 функций 𝑓 ∈ 𝐵(𝑟)2 . Выясняется связь доказанной теоремы с поведением точных констант в неравенстве Джексона-Стечкина для модулей непрерывности 𝜔𝑚(𝑓(𝑟), 𝑡)2. Для класса функций 𝑊(𝑟)
𝑚 (Φ)2, определённой заданной монотонно возрастающей мажорантой Φ, удовлетворяющей некоторым ограничениям, вычислены точные значения различных 𝑛-поперечников в пространстве 𝐵2.