On the theory of two-dimensional singular integral operators and its applications to boundary value problems for elliptic systems of equations
https://doi.org/10.22405/2226-8383-2024-25-5-74-89
Abstract
In a Lebesgue space with weight (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2), where 𝐷 is a finite singly connected domain of the complex plane bounded by a simple closed Lyapunov curve Γ and containing the point 𝑧 = 0, we consider a two-dimensional singular integral operator of the Mikhlin – Calderon – Zygmund type of the form
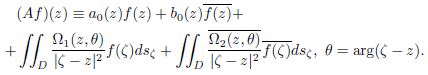
Depending on the homotopy class M𝜈(𝜈 = 0,±1, . . . ,±𝑚) of the operator 𝐴, we establish effective necessary and sufficient conditions for the operator 𝐴 to be Noetherian in (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2) and found formulas for calculating the index of an operator.
The results obtained are applied to the Dirichlet and Neumann problems for general elliptic systems of two equations with two higher-order independent variables.
About the Authors
Gulkhoja Jangibekov
A. Dzhuraev Institute of Mathematics
Tajikistan
Tajikistan
doctor of physical and mathematical sciences
Gulnazar Mavlonazarovich Koziev
International University of tourism and entrepreneurship of Tajikistan
Tajikistan
Tajikistan
candidate of physical and mathematical sciences
References
1. Nother F., 1921, “Uber eine Klasse singularer Integralgleichungen”, Math. Ann., 82, pp. 42 – 63.
2. Carleman T. 1922, “Sur la resolution de certaines equations integrales”, Ark. Math., 16, vol 26, pp. 1 – 19.
3. Muskelishvili N. I. 1968, “Singular integral equation”, М.; Nauka, 511 p. (English transl.:
4. Noordh., Groningen, 1953.)
5. Тricomi F. G. 1926, “Formula d’inversione dell’ordine di due integrazioni doppie “con asterisco” ”, Rend. Accad. Naz. Lincei, III, ser. 6a, fasc. 9, pp. 535 – 539.
6. Тricomi F. G. 1928, “Equazioni integrall contenenti il valor principale di un integrale doppio”, Math. Z., 27, pp. 87 – 133.
7. Giraund G. 1934, “Equations a integrales principales”, Ann. Scient. Ecole norm. super., 51,
8. fasc. 3 et, pp. 251 – 372.
9. Giraund G. 1936, “Sur une classe generale d’equations a interrales principales”, C. r. Acad. sci., 202, vol 26, pp. 2124 – 2126.
10. Calderon А. P. and Zygmund A., 1956, “On singular integrals”, Amer. J. Math., 78, vol 2,
11. pp. 289 – 309.
12. Mikhlin С. Г. 1962, “Multidimensional singular integrals and integral equations”, Fizmatgiz,
13. Moscow (Russian);(English transl.: Pergamon Press, New York 1965.)
14. Gocheberg I. Z. 1960, “On the theory of multidimensional singular integral equations “.
15. C. R. (Dokl.) Acad. Sci. USSR, n. Ser., 133, vol. 6, pp. 1279 – 1282(Russian).
16. Simonenko I. B . 1965, “A new general method for the investigatoin of linear operator integral equations“. (Russian).“. I. Izv. Akad.Nauk SSSR, Ser. Mat.. I-II, 29, vol. 3, 4, 567 – 580, pp. 757 – 782. (Russian)
17. Duduchava R. 1984, “On multidimensional singular integral operators“. I-II,Journal of Operator Theory, 11, 1984, 41 – 76, pp. 199 – 214.
18. Stein E. M. 1957, “Note on singular integrals” Proc. Amer. Math. Soc.. vol. 8. pp. 250 – 254.
19. Vekua И. N. 1959, “Generalized Analytic Functions”, M.: Fizmat. 628 p. (Russian) (English transl.: Pergamon Press, Oxford, 1962.)
20. Vekua И. N. 1948, “New methods of solving elliptic equations”, М.-L: Теkh.lit., 298 p.(Russian) (English transl.:North Holland, Amsterdam, 1967.)
21. Dzuraev А.D. 1971, “On the one method of Singular Integral Equations on a boudeddomain ”, Dokl. Acad. Sci. USSR, т. 197, vol 46, pp. 1251 – 1254 (Russian).
22. Dzhuraev А. D. 1987, “ Method of Singular Integral Equations”, М.: Наука (Russian) Longman, Harlow, 1992. 1987, 415 с.(English transl.:Longman, Harlow, 1992).
23. Bojarski B. 1960, “ Studies on elliptic equations in plane domains and boundary value problems of function theory. Dr. sci. thesis, Steklov Inst. Math., Moscow (Russian).
24. Komyak I. I. 1978, “The noether property and the index of a class of two-dimensional singular integral equations”, Dokl. Acad. Sci. BSSR, Ser. 22, vol 6, pp. 488 – 491 (Russian).
25. Komyak I. I. 1980, “The noether property and the index of a class of two-dimensional singular integral equations in the ”, Differential equations, Ser. 16, vol 2, pp. 328 – 343 (Russian).
26. Bilman B. М., & Dzangibekov G. 1986, “Noethericity conditions and index for some twodimensional singular integral equations with discontinuous coefficients over a bounded simply connected domain”, Dokl. Acad. Sci. USSR, Ser. 288, vol 4, p. 792 – 797.(Russian) (English transl.:Soviet Math. Dokl. 33 vol. 3, pp. 752 – 757.)
27. Boimatov К. H., & Dzangibekov G. 1988, “On a singular integral operator”, Uspekhi math.nauk 43, vup. 3 (261), pp. 171 – 172. (Russian) (English transl.: Math. Surveys 43 (1988), vol 3, pp. 199 – 200.).
28. Dzangibekov G. 1988, “On the Noethericity and index of a class of two – dimensional singular integral equation with discontinuous coefficients” Dokl. Acad. Sci. USSR, Ser.300,vol 42, pp. 272 – 276.(Russian) (English transl.: Soviet Math. Dokl. 37 1988, vol 3, pp. 639 – 643.)
29. Dzangibekov G. 1993, “On a class of two – dimensional singular integral operators and
30. its applications to boundary value problems for elliptic systems of equations in the plane”,
31. Dokl.Akad.Nauk 330, no.4, pp. 415–419. (Russian). (English transl.: Russian Acad. Sci. Dokl.
32. Math. 47, (1993), no 3, pp. 498 – 503.)
33. Dzangibekov G. 2002 “On some two-dimensional singular integral operators on a bounded domain”, Dokl.Akad.Nauk, т. 383, vol 1, pp. 415 – 419.(Russian) (English transl.:Russian Acad. Sci. Dokl. Math., 2002)
34. Dzangibekov G., & Khudzhanazarova G. Kh. 2004, “On the Noethericity and index of some two-dimensional singular integral operators over bounded domain”, Dokl.Akad.Nauk, 396, no 4,
35. pp. 449 – 454.(Russian) (English transl.:Russian Acad. Sci. Dokl. Math., 2004)
36. Dzangibekov G., & Khudzhanazarova G. Kh. 2004, “On the Dirichlet problem for an elliptic system of two fourth-order equations on a plane”, Dokl.Akad.Nauk 398, vol 2, 2004, с. pp. 151 – 155.(Russian) (English transl.:Russian Acad. Sci. Dokl. Math., 2004).
37. Dzangibekov G., & Valiev N. G. 2014, “On some two-dimensional singular integrals operators with characteristics depending on the pole”, Dokl. Acad. Sci. Taj., Ser. 57, vol 7, pp. 556 – 562.(Russian).
38. Dzangibekov G., & Koziev G. M. 2015, “The Noetherian conditions and the index of some class of singular integral operators over a bounded simply connected domain”, Dokl. Acad. Sci. Taj., т. 58, vol 10, pp. 886 – 893. (Russian).
39. Dzangibekov G., & Одинабеков Д . М., & Khudzhanazarova G. Kh. 2019, “On the Noetherian conditions and the index of some class of singular integral operators over a bounded simply connected domain”, Moscow University Mathematics Bulletin, 74:2 (2019), 49 – 54. Ser.
40. (Russian). (English transl.:Moscow University Mathematics Bulletin Маthем., меh., vol 2,
41. pp. 9 – 14).(Russian).
42. Dzangibekov G., & Odinabekov D. M. 2019, “The Noetherian conditions and the index of
43. some class of singular integral operators over a bounded simply connected domain”, On Sat.
44. Modern problems of mathematics and mechanics. Moscow State University M.V. Lomonosov,
45. pp. 50 – 53.(Russian).
46. Vekua N. P. 1970, “Systems of singular integral equations and some boundary problems”, M.: Science, 379 p.
47. Begehr H., & Vanegas C. J., 2006, “Iterated Neumann problem for higher order Poisson
48. equation”, Math. Nachr. 279, pp. 38 – 57.
Review
For citations:
Jangibekov G., Koziev G.M. On the theory of two-dimensional singular integral operators and its applications to boundary value problems for elliptic systems of equations. Chebyshevskii Sbornik. 2024;25(5):74-89. (In Russ.) https://doi.org/10.22405/2226-8383-2024-25-5-74-89
Views:
330
Email this article 