К теории двумерных сингулярных интегральных операторов и его приложениях к краевым задачам для эллиптических систем дифференциальных уравнений
https://doi.org/10.22405/2226-8383-2024-25-5-74-89
Аннотация
В лебеговом пространстве с весом (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2), где 𝐷 – конечная
односвязанная область комплексной плоскости, ограниченная простой замкнутой кривой
Ляпунова Γ, и содержащая внутри точку 𝑧 = 0, рассматривается двумерный сингулярный
интегральный оператор типа Михлина – Кальдерона – Зигмунда вида
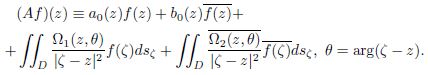
В зависимости от гомотопического класса M𝜈(𝜈 = 0,±1, . . . ,±𝑚) оператора 𝐴 установлены эффективные необходимые и достаточные условия нётеровости оператора 𝐴 в (𝐿^𝑝)_𝛽−2/𝑝(𝐷) (1 < 𝑝 < ∞, 0 < 𝛽 < 2) и найдены формулы для подсчёта индекса оператора.
Полученные результаты применяются к задачам Дирихле и Неймана для общих эллиптических систем двух уравнений с двумя независимыми переменными высшего порядка.
Об авторах
Гулходжа Джангибеков
Институт математики им. А. Джураева НАН Таджикистана
Таджикистан
Таджикистан
доктор физико-математических наук
Гулназар Мавлоназарович Козиев
Международный университет туризма и предпринимательства Таджикистана
Таджикистан
Таджикистан
кандидат физико-математических наук
Список литературы
1. Nother F., Uber eine Klasse singularer Integralgleichungen // Math. Ann., 1921, 82, 42 – 63.
2. Carleman T., Sur la resolution de certaines equations integrales // Ark. Math., 1922, 16, №
3. , 1–19.
4. Мусхелишвили Н.И. Сингулярные интегральные уравнения // М.; Наука, 1968, 511 с.
5. Тricomi F.G. Formula d’inversione dell’ordine di due integrazioni doppie ′′con asterisco′′ //
6. Rend. Accad. Naz. Lincei, III, ser. 6a, fasc. 9, 1926, 535 – 539.
7. Тricomi F.G. Equazioni integrall contenenti il valor principale di un integrale doppio // Math.
8. Z., 27, 1928, 87 – 133.
9. Giraund G. Equations a integrales principales // Ann. Scient. Ecole norm. super., 51, fasc. 3 et, 1934, 251 – 372.
10. Giraund G. Sur une classe generale d’equations a interrales principales //C. r. Acad. sci., 202, № 26, 1936, 2124 – 2126.
11. Calderon А. P. and Zygmund A., On singular integrals // Amer. J. Math., 78, № 2, (1956),
12. – 309.
13. Михлин С.Г. Многомерные сингулярные интегралы и интегральные уравнения // М.: Физматгиз, 1962, 254 с.
14. Гохберг И.Ц. К теории многомерных сингулярных интегральных уравнений // ДАН
15. СССР, 133, № 6, 1960, 1279 – 1282.
16. Симоненко И.Б. Новый общий метод исследования линейных операторных уравнений типа сингулярных интегральных уравнений // Изв. АН СССР, сер. матем. I-II, т. 29, № 3, 4, 1965, с. 567 – 580, 757 – 782.
17. Duduchava R. On multidimensional singular integral operators. I-II // Journal of Operator
18. Theory, 11, 1984, 41 – 76, 199 – 214.
19. Stein E.M. Note on singular integrals // Proc. Amer. Math. Soc.. 1957, vol. 8. p. 250–254.
20. Векуа И.Н. Обобщенные аналитические функции // М.: Физматгиз, 1959, 628 с.
21. Векуа И.Н. Новые методы эллиптических уравнений // М.-Л: Тех.лит, 1959, 298 с.
22. Джураев А.Д. Об одном методе исследования сингулярных интегральных уравнений по ограниченной области // ДАН СССР, т. 197, № 46, 1971, с. 1251 – 1254.
23. Джураев А.Д. Метод сингулярных интегральных уравнений // М.: Наука, 1987, 415 с.
24. Боярский Б.В. Исследования по уравнениям эллиптического типа на плоскости и граничным задачам теории функций // Дисс. докт. физ.-мат. наук. Москва, 1960.
25. Комяк И.И. Об условиях нетеровости и формуле индекса одного класса сингулярных интегральных уравнений // Докл. АН БССР, т. 22, № 6, 1978, c. 488 – 491.
26. Комяк И.И. Условия нетеровости и формула индекса одного класса сингулярных интегральных уравнений по круговой области // Дифференц. уравнения, 1980, том 16, № 2, 328 – 34
27. Бильман Б.М., Джангибеков Г. Об условиях нетеровости и индексе некоторых двумерных сингулярных интегральных уравнений с разрывными коэффициентами по ограниченной односвязной области // ДАН СССР, т. 288, № 4, 1986, с. 792 – 797.
28. Бойматов К.Х., Джангибеков Г. Об одном сингулярном интегральном операторе // Успехи математических наук. т. 43, вып.3 (261), 1988, с. 171 – 172.
29. Джангибеков Г. О нетеровости и индексе некоторых двумерных сингулярных интегральных операторов // ДАН СССР, т. 300,№ 42, 1988, с. 272 – 276.
30. Джангибеков Г. Об одном классе сингулярных интегральных операторов и его приложениях к краевым задачам для эллиптических систем на плоскости // ДАН СССР, т. 330, № 4, 1993, с.415 – 419.
31. Джангибеков Г. О некоторых двумерных сингулярных интегральных операторах по ограниченной области // ДАН СССР, т. 383, № 1, 2002, с. 7 – 9. 415 – 419.
32. Джангибеков Г., Худжаназарова Г.Х. О нетеровости и индексе некоторых двумерных сингулярных интегральных операторов по ограниченной области // ДАН России, т. 396, № 4, 2004, с. 449 – 454.
33. Джангибеков Г., Худжаназарова Г.Х. О задаче Дирихле для эллиптической системы двух уравнений четвертого порядка на плоскости // ДАН России, т. 398, № 2, 2004, с. 151 – 155.
34. Джангибеков Г., Валиев Н.Г. О некоторых двумерных сингулярных интегральных операторов с характеристиками зависящими от полюса // ДАН РТ, т. 57, № 7, 2014, c. 556 – 562.
35. Джангибеков Г., Козиев Г.М. Об одном двумерном сингулярном интегральном операторе с нечетной характеристикой // ДАН РТ, т. 58, № 10, 2015, c. 886 – 893.
36. Джангибеков Г., Одинабеков Д.М., Худжаназарова Г.Х. Об условиях нётеровости и индексе одного класса сингулярных интегральных операторов по ограниченной односвязной области // Вестник Московского университета. Сер. 1. Матем., мех., 2019, № 2, c. 9 – 14.
37. Джангибеков Г., Одинабеков Д.М. К теории Нетера двумерных сингулярных интегральных операторов с четной характеристикой по ограниченной области // В сб. Современные проблемы математики и механики. МГУ им. М.В. Ломоносова, 2019, с. 50 – 53.
38. Векуа Н.П. Системы сингулярных интегральных уравнений и некоторые граничные задачи // М.: Наука, 1970, 379 с.
39. Begehr H., Vanegas C.J., Iterated Neumann problem for higher order Poisson equation // Math. Nachr. 279 (2006) 38–57.
Рецензия
Для цитирования:
Джангибеков Г., Козиев Г.М. К теории двумерных сингулярных интегральных операторов и его приложениях к краевым задачам для эллиптических систем дифференциальных уравнений. Чебышевский сборник. 2024;25(5):74-89. https://doi.org/10.22405/2226-8383-2024-25-5-74-89
For citation:
Jangibekov G., Koziev G.M. On the theory of two-dimensional singular integral operators and its applications to boundary value problems for elliptic systems of equations. Chebyshevskii Sbornik. 2024;25(5):74-89. (In Russ.) https://doi.org/10.22405/2226-8383-2024-25-5-74-89
Просмотров:
334
Послать статью по эл. почте 