Transcendence of certain 2-adic numbers
https://doi.org/10.22405/2226-8383-2023-24-5-237-243
Abstract
We prove here that at least one of the two 2-adic numbers which are the values at 𝑧 = 1 of the sums in Q_2 of the series
where 𝜆 is a certain polyadic Liouville number. The series considered converge in any field Q_𝑝. We deal here with Q_2. The symbol (𝛾)𝑛 denotes Pochhammer symbol, i.e. (𝛾)0 = 1 , and for 𝑛 ≥ 1 we have (𝛾)_𝑛 = 𝛾(𝛾 + 1)...(𝛾 + 𝑛 − 1). The values of these series were also calculated at polyadic Liouville number. The canonic expansion of a polyadic number 𝜆 is of the form
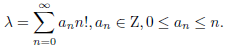This series converges in any field of 𝑝− adic numbers Q_𝑝 .
We call a polyadic number 𝜆 a polyadic Liouville number, if for any 𝑛 and 𝑃 there exists a positive integer 𝐴 such that for all primes 𝑝, satisfying 𝑝 ≤ 𝑃 the inequality
holds.
It was proved earlier that the Liouville polyadic number is transcendental in any field Q_𝑝.
In other words,the Liouville polyadic number is globally transcendental. It allowed to prove using some equality that there exists an infinite set of 𝑝−adic fields Q_𝑝 where at least one of
the numbers 𝑓_0(𝑧), 𝑓_1(𝑧). Here we prove the transcendence of values in the field Q_2.
About the Author
Vladimir Grigor’evich Chirskii
Lomonosov Moscow State University; Russian Presidential Academy of National Economy and Public Administration
Russian Federation
Russian Federation
doctor of physical and mathematical sciences
References
1. Shidlovskii, A. B. 1989, “Transcendental Numbers”, W.de Gruyter.-Berlin.-New York.467pp.
2. Adams. W. 1990, “On the algebraic independence of certain Liouville numbers”,J.Pure and Appl.Algebra., Vol, 13, pp.41-47.
3. Waldschmidt. M. 1990, “Independance algebrique de nombres de Liouville”, Lect.Notes Math., Vol, 1415, pp.225-235.
4. Chiskii V. G. 2020, “Arithmetic Properties of Euler-Type Series with a Liouvillean Polyadic Parameter”, Dokl. Math., Vol.102,no.2. pp.412-413.
5. Chiskii V. G.,2021, “ Arithmetic properties of values at polyadic Liouvillean point of Euler-type series with polyadic Liouvillean parameter”, Chebyshevsky sbornik, Vol. 22, no.2, pp.304-312.
6. Chiskii V. G. 2006, “Generalization of the Notion of a Global Relation”, J. Math. Sci(N.Y), Vol.137, no.2, pp.4744-4754.
7. Chiskii V. G.V. G. 1994, “Qn series which are algebraically independent in all local fields”, Vestn.Mosc.univ.Ser.1.,Math.,mech., n0.3, pp.93-95.
8. Chirskii V. G. 2019, “Product Formula, Global Relations and Polyadic Integers”, Russ. J. Math. Phys., Vol.26, no.3, pp.286-305.
9. Chirskii V. G. 2020, “ Arithmetic properties of generalized hypergeometric F- series”, Russ. J. Math. Phys., Vol.27, no.2, pp.175-184.
10. Chirskii V. G. 2022, “ Arithmetic properties of the values of generalized hypergeometric series with polyadic transcendental parameter”, Dokl. Math., Vol. 106, no.2, pp.386-397
11. Yudenkova E.Yu. 2021, “ Infinite linear and algebraic independence pf values of F-series at polyadic Liouvillean point”, Chebyshevsky sbornik, Vol. 22, no.2, pp.334-346.
12. Matveev V.Yu. 2019, “ Properties of elements of direct products of fields”, Chebyshevsky sbornik, Vol. 20, no.2, pp.383-390.
13. Krupitsin E. S. 2019, “ Arithmetic properties of series of certain classes”, Chebyshevsky sbornik, Vol. 20, no.2, pp.374-382.
14. Ernvall-Hytonen A.-M.;Matala-aho T.;Seppala I. 2023, “ Euler’s factorial series, Hardy integral, and continued fractions”, J.Number Theory, Vol. 244, pp.224-250.
15. Chirskii V. G. 2023, “Transcendence of p-adic values of generalized hypergeometric series with transcendental polyadic parameter”, Dokl. Math., Vol. 107, no.2, pp.109-111.
16. Chirskii V. G. 2021, “ Polyadic Liouvillean numbers”, Chebyshevsky sbornik, Vol. 22, no.3, pp.245-255.
Review
For citations:
Chirskii V.G. Transcendence of certain 2-adic numbers. Chebyshevskii Sbornik. 2023;24(5):237-243. (In Russ.) https://doi.org/10.22405/2226-8383-2023-24-5-237-243
Views:
330
Email this article 