Трансцендентность некоторых 2-адических чисел

Аннотация

В работе доказывается трансцендентность в поле 2-адических чисел хотя бы одного из двух 2-адических чисел, представляющих собой суммы в поле Q_2 рядов типа Эйлера

где 𝜆 представляет собой некоторое полиадическое лиувиллево число, 𝑧 = 1. Как обычно, символ Похгаммера обозначается (𝛾)𝑛 , по определению, (𝛾)_0 = 1 , а при 𝑛 ≥ 1 имеем (𝛾)_𝑛 = 𝛾(𝛾 + 1)...(𝛾 + 𝑛 − 1). Рассматриваемые ряды сходятся в любом поле Q_𝑝 . Мы
рассматриваем поле Q_2. Параметром рассматриваемых рядов типа Эйлера является полиадическое чмсло Лиувилля. Напомним, что каноническое разложение полиадического числа 𝜆 имеет вид

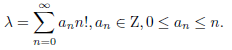Этот ряд сходится в любом поле 𝑝− адических чисел Q_𝑝 . Будем называть полиадическое число 𝜆 полиадическим числом Лиувилля (или лиувиллевым полиадическим числом), если для любых чисел 𝑛 и 𝑃 существует натуральное число 𝐴 такое, что для всех простых чисел 𝑝 , удовлетворяющих неравенству 𝑝 ≤ 𝑃 выполнено неравенство

Ранее было доказано простое утверждение о том, что полиадическое число Лиувилля является трансцендентным элементом любого поля Q_𝑝. Иными словами, полиадическое
число Лиувилля - глобально трансцедентное число. Это позволяет, используя некоторое тождество для обобщённых гипергеометрических рядов и предыдущие результаты автора
доказать, что существует бесконечное множество полей Q_𝑝 , в которых трансцендентностно хотя бы одно из значений рядов 𝑓_0(𝑧), 𝑓_1(𝑧). В этой работе доказывается трансцендентность
значений в конкретном поле Q_2.