Kolmogorov’s type inequalities in Bergman space 𝐵2 and some of its applications

Abstract

Let N be the set of natural numbers, Z_+ be the set of non-negative integers, C be the set of complex numbers, 𝐴(𝑈) be the set of analytic functions in the unit circle 𝑈 := {𝑧 ∈ C : |𝑧| < 1}, 𝐵_2 – be the Bergman spaces of functions 𝑓 ∈ 𝐴(𝑈), endowed with a finite norm 

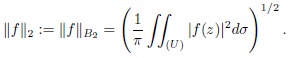For 𝑓 ∈ 𝐴(𝑈), we denote the usual derivative of order 𝑚 ∈ N by 𝑓(𝑚)(𝑧) and introduce a class of functions

Let 𝐸_(𝑛−1)(𝑓)_2 be the magnitude of the best approximation of function 𝑓 ∈ 𝐵_2 by complex algebraic polynomials of degree ≤ 𝑛 − 1. In this paper, a number of exact inequalities are found between the value of the best approximation of intermediate derivatives 𝐸__(𝑛−𝜈−1)(𝑓^(𝜈))_2 (𝜈 = 1, 2, · · · ,𝑚 − 1;𝑚 ≥ 2) and the best approximation 𝐸(_𝑛−𝑚−1)(𝑓^(𝑚))_2 of the highest derivative 𝑓(𝑚). Let 𝑊^(𝑚)_2 := 𝑊^(𝑚)_2 (𝑈) (𝑚 ∈ N) be a class of functions 𝑓 ∈ 𝐵^(𝑚)
2 for which ‖𝑓^(𝑚)‖_2 ≤ 1. In this paper is proved that for any 𝑛,𝑚 ∈ N, 𝜈 ∈ Z+, 𝑛 > 𝑚 ≥ 𝜈, the equality of takes place

and also, in the space 𝐵2 for functions 𝑓 ∈ 𝐵^(𝑚)_2 for all 1 ≤ 𝜈 ≤ 𝑚 − 1,𝑚 ≥ 2, an exact inequality of the Kolmogorov type

is found, where the constant 𝐴𝑚,𝜈(𝑛) is explicitly written out. Some applications of the resulting inequality are given.