Цепная дробь [0; 𝑎1, 1, 𝑎3, ..., 𝑎𝑛] и её ступенчатая аппроксимация

Пусть 𝑂𝑋𝑌 — прямоугольная система координат с целочисленной решеткой, 𝐴𝐵 — отрезок с целыми (целочисленными) концами 𝐴 = (𝑞; 0)𝑂𝑋𝑌 = 𝐴(𝑞) и 𝐵 = (0; 𝑝)𝑂𝑋𝑌 = 𝐵(𝑝), такими, что 𝑝 и 𝑞 взаимно просты, а разложение 𝑝 𝑞 в цепную дробь имеет вид [0; 𝑎1, 1, 𝑎3,
. . . , 𝑎2𝑁′+1], где 𝑎−1 , 𝑎3, . . . , 𝑎2𝑁′+1, 𝑁′, 𝑝, 𝑞, ∈ N : (= {1, 2, . . .}).
Рассмотрим множество S𝐴𝐵 таких единичных квадратов (клеток) этой решетки, что внутренность каждого из них имеет непустое пересечение с 𝐴𝐵. Границу этого множества
представим в виде объединения ломаных S−𝐴𝐵 и S+
𝐴𝐵 таких, что их крайними вершинами служат точки 𝐴 и 𝐵. Здесь индекс минус (плюс) указывает на то, что S− 𝐴𝐵 (S+
𝐴𝐵) лежит по левую (правую) сторону от отрезка 𝐴𝐵 при движение от 𝐴 к 𝐵. Ломаную S− 𝐴𝐵 (S+ 𝐴𝐵) назовем левой (правой) (целочисленной) ступенчатой аппроксимацией отрезка 𝐴𝐵 или цепной дроби [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁]. Для краткости такие ломаные будем называть маршами, а их горизонтальные звенья — ступенями, вертикальные —
высотами, что вызвано ассоциацией с лестничным маршем.
В работе получены следующие результаты:
1. Формулы целочисленной аппроксимации цепной дроби, как конечных, так и бесконечных.
2. Алгоритмическое построение маршей S±
𝐴𝐵, определяемое рассматриваемой цепной
дробью, дает их аналитическое задание через марши векторов-слагаемых из второго равенства:

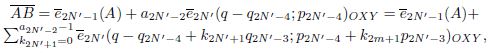
где векторы 𝑒2𝑁′−1 = (−𝑞2𝑁′−4; 𝑝2𝑁′−4)𝑂𝑋𝑌 и 𝑒2𝑁′ = (−𝑞2𝑁′−3; 𝑝2𝑁′−3)𝑂𝑋𝑌 , координаты которых определяются подходящими дробями 𝑝𝑛−3/𝑞𝑛−3 порядка 𝑛 = 2𝑁′ − − 1, 2𝑁′, исходной цепной дроби, а в скобках указаны точки приложения векторов.
3. Расположение ступеней ширины 𝑎1 в S− 𝐴𝐵, устанавливается с помощью семейства параллельных переносов отрезка с концами (𝑞 − 𝑎1; 0)𝑂𝑋𝑌 и (𝑞 − 1; 0)𝑂𝑋𝑌 . Каждый член семейства находим через аппроксимационные формулы для [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁].
4. Формула, дающая количество ступеней ширины 𝑎1 в S−
𝐴𝐵, представляет собой трехдиагональный определитель (2𝑁′ −5)-го порядка: главная диагональ состоит из элементов 𝑎4, 1, 𝑎5, . . . , 𝑎2𝑁′−6, верхняя диагональ — из единиц, нижняя из минус единиц, а остальные нули.

1. Хинчин А. Я. Цепные дроби. — М.: Наука, 1978. — 112 с.

2. Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966. — 376 с.

3. Нестеренко Ю. В. Теория чисел. — М.: Академия, 2008. — 272 с.

4. Нестеренко Ю. В., Никишин Е. М. Очерк о цепных дробях // Квант. — 1983. — № 5. — С. 16–20; № 6. — С. 26–30.

5. Михалович Ш. Х. Теория чисел. — М.: Высшая школа, 1967. — 336 с.

6. Энциклопедия элементарной математики. Книга 1. Арифметика / под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.–Л.: ГИТТЛ, 1951. — 448 с.

7. Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений. — М.: Наука, 1978. — 304 с. — URL: https://libcats.org/book/504157 (дата обращения: 01.01.2024).

8. Арнольд В. И. Цепные дроби. — М.: МЦНМО, 2001. — 40 с. — (Математическое просвещение; вып. 14). — URL: https://www.mccme.ru/mmmf-lectures/books/books/book.14.pdf (дата обращения: 01.01.2024).

9. Karpenkov O. Geometry of Continued Fractions. — Heidelberg: Springer, 2013. — xviii, 405 p. — (Algorithms and Computation in Mathematics; vol. 26).

10. Герман О. Н. Геометрия цепных дробей // Байкальские чтения. — Иркутск, 2016. — URL: https://www.youtube.com/watch?v=h9bglrhFpr8 (дата обращения: 01.01.2024).

11. Klein F. Ausgewahlte Kapitel der Zahlentheorie. — Leipzig: Teubner, 1907. — 364 p.

12. Коркина В. И. Двумерные цепные дроби. Самые простые примеры // Труды МИАН. — 1995. — Т. 209. — С. 143–166. — URL: https://www.mathnet.ru/links/95f8a9601d2ed7a26c463967fed6e473/tm1172.pdf (дата обращения: 01.01.2024).

13. Галламов М. М. О некоторых подходах к решению задачи С. В. Конягина о шахматной раскраске // Материалы научно-исследовательского семинара по дискретной геометрии и геометрии чисел / под рук. Н. П. Долбилина и др. — М.: МГУ, 2024. — С. 1–8. — URL: http://new.math.msu.su/department/dm/data/uploads/diskrgeom/gallamov_doklad_dg_gch16-4-2024.pdf (дата обращения: 01.01.2024).

14. Галламов М. М. Прямые 𝑦 = −𝑒 · 𝑥 + 𝑡 и шахматная раскраска // Алгебра, теория чисел и дискретная геометрия: современные проблемы, приложения и проблемы истории: материалы XVI Междунар. конф., посв. 80-летию проф. М. Деза. — Тула, 2019. — С. 247–250.

15. Галламов М. М. Прямые 𝑦 = 1−√5/2 · 𝑥 + 𝑠 и шахматная раскраска // Алгебра, теория чисел и дискретная геометрия: современные проблемы, приложения и проблемы истории: материалы XVII Междунар. конф. — Тула, 2019. — С. 247–250.

16. Галламов М. М. Прямые 𝑦 = −[𝑎±0 ; 𝑎±1 , 𝑎±2 , . . .]·𝑥+𝑡 с четными 𝑎+𝑛 и нечетными 𝑎−𝑛 = 𝑎(̸= 1) и шахматная раскраска // Алгебра, теория чисел и дискретная геометрия: современные проблемы, приложения и проблемы истории: материалы XVIII Междунар. конф. — Тула, 2020. — С. 261–265.

17. Галламов М. М. Целочисленная аппроксимация отрезка // Чебышевский сборник. — 2022.

18. — Т. 23, вып. 4. — С. 20–38. — URL: https://www.mathnet.ru/links/

19. a67f15bac6686abfb4000f5d3c545/cheb1220.pdf (дата обращения: 01.01.2024).

20. Шишкин Ю. А. Эйлерова характеристика. — М.: Наука, 1984. — 96 с. — (Популярные лекции по математике; вып. 58). — URL: http://www.math.ru/lib/book/plm/v58.djvu (дата обращения: 01.01.2024).

21. Васильев Н. Б. Вокруг формулы Пика // Квант. — 1974. — № 12. — С. 39–43.

22. Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.

23. Grunbaum B., Shephard G. C. Pick’s Theorem // The American Mathematical Monthly. — 1993. — Vol. 100, no. 2. — P. 150–161.

24. Клейн Ф. Элементарная математика с точки зрения высшей. Арифметика. Алгебра. Анализ. — 4-е изд. — М.: Наука, 1987. — Т. 1. — 432 с.

25. Дэвенпорт Г. Высшая арифметика. Введение в теорию чисел. — М.: Наука, 1965. — 176 с.

26. Сизый С. В. Лекции по теории чисел: учеб. пособие для студентов вузов. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2008. — 192 с. — ISBN 978-5-9221-0741-9.

27. Khovanova T., Konyagin S. Sequences of Integers with Missing Quotients and Dense Points Without Neighbors // arXiv [Электронный ресурс]. — 2011. — URL: https://arxiv.org/abs/1104.0441 (дата обращения: 01.01.2024).