Chain fraction [0; 𝑎1, 1, 𝑎3, ..., 𝑎𝑛] and its stepwise approximation

Let 𝑂𝑋𝑌 be a rectangular coordinate system with an integer lattice, 𝐴𝐵 is a segment with integer ends 𝐴 = (𝑞; 0)𝑂𝑋𝑌 = 𝐴(𝑞) and 𝐵 = (0; 𝑝)𝑂𝑋𝑌 = 𝐵(𝑝) such that the decomposition of 𝑝
𝑞 into a continued fraction has the form [0; 𝑎1, 1, 𝑎3, . . . , 𝑎2𝑁′+1], where 𝑎− 1 , 𝑎3, . . . , 𝑎2𝑁′+1, 𝑁′, 𝑝, 𝑞,𝑁′ ∈ N : (= {1, 2, . . .}), moreover, 𝑝 and 𝑞 are mutually simple.
Consider the set S𝐴𝐵 of such unit squares (cells) of this lattice, that the interior of each of them has a nonempty intersection with 𝐴𝐵. The boundary of this set is represented as a union
of polylines S− 𝐴𝐵 and S+ 𝐴𝐵 such that their extreme vertices are the points 𝐴 and 𝐵. Here, the minus index (plus) indicates that S− 𝐴𝐵 (S+ 𝐴𝐵) lies on the left (right) side of the segment 𝐴𝐵
when moving from 𝐴 to 𝐵.
Polyline S− 𝐴𝐵 (S+ 𝐴𝐵)let’s call left (right) (integer) stepwise approximation of the segment 𝐴𝐵 or continued fraction [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁]. For brevity, we will call such polylines marches, and
their horizontal links—steps, vertical ones—heights, which is caused by association with a flight of stairs. The following results were obtained in the work:
1. Formulas for integer approximation of the stucco fraction, both finite and infinite.
2. Algorithmic construction of marches S± 𝐴𝐵, determined by the considered chain fraction. gives their analytical task through the marches of vectors-terms of the second equality:

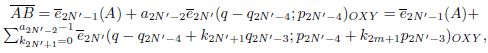
where the vectors 𝑒2𝑁′−1 = (−𝑞2𝑁′−4; 𝑝2𝑁′−4)𝑂𝑋𝑌 and 𝑒2𝑁′ = (−𝑞2𝑁′−3; 𝑝2𝑁′−3)𝑂𝑋𝑌 , whose coordinates are determined by suitable fractions 𝑝𝑛−3/𝑞𝑛−3 of the order 𝑛 = 2𝑁′− − 1.2𝑁′, the original continued fraction, and the points of application of the vectors are indicated in parentheses.
3. The location of the steps of width 𝑎1 in S− 𝐴𝐵, is set using a family of parallel transfers of a segment with ends (𝑞 − 𝑎1; 0)𝑂𝑋𝑌 and (𝑞 − 1; 0)𝑂𝑋𝑌 . We find each member of the family through approximation formulas for [0; 𝑎1, 1, 𝑎3, . . . , 𝑎𝑁].

4. The formula giving the number of steps of width 𝑎1 in S−
𝐴𝐵 is a tridiagonal determinant (2𝑁′ − 5)-th order: the main diagonal consists of elements 𝑎4, 1, 𝑎5, . . . , 𝑎2𝑁′−6,the upper
diagonal is — of ones, the lower one is minus ones, and the rest are zeros.

1. Khinchin, A. Ya. 1978, Tsepnye drobi [Continued Fractions], 4th ed, Moscow: Nauka, 112 p.

2. Bukhshtab, A. A. 1966, Teoriya chisel [Number Theory], Moscow: Prosveshchenie, 376 p.

3. Nesterenko, Yu. V. 2008, Teoriya chisel [Number Theory], Moscow: Akademiya, 272 p.

4. Nesterenko, Yu. V, Nikishin, E. M. 1983, “Ocherk o tsepnykh drobyakh” [Essay on Continued Fractions], Kvant, 5, pp. 16–20; 6, pp. 26–30.

5. Mikhalovich, Sh. Kh. 1967, Teoriya chisel [Number Theory], Moscow: Vysshaya Shkola, 336 p.

6. Aleksandrov, P. S, Markushevich, A. I, Khinchin, A. Ya. 1951, Entsiklopediya elementarnoy matematiki. Kniga 1. Arifmetika [Encyclopedia of Elementary Mathematics. Book 1. Arithmetic], Moscow-Leningrad: GITTL, 448 p.

7. Arnold, V. I. 1978, Dopolnitel’nye glavy teorii obyknovennykh differential’nykh uravneniy [Additional Chapters of Ordinary Differential Equations Theory], Moscow: Nauka, 304 p.

8. Arnold, V. I. 2001, Tsepnye drobi [Continued Fractions], Moscow: MCCME, 40 p.

9. Karpenkov, O. 2013, Geometry of Continued Fractions, Heidelberg: Springer, 405 p.

10. German, O. N. 2016, “Geometriya tsepnykh drobey” [Geometry of Continued Fractions], Baikal Readings [Online], Available at: https://www.youtube.com/watch?v=h9bglrhFpr8

11. Klein, F. 1907, Ausgewahlte Kapitel der Zahlentheorie, Leipzig: Teubner, 364 p.

12. Korkina. V. I. 1995, “Dvumernye tsepnye drobi. Samye prostye primery” [Two-dimensional Continued Fractions. Simplest Examples], Trudy MIAN, 209, pp. 143–166.

13. Gallamov, M. M. 2024, “O nekotorykh podkhodakh k resheniyu zadachi S.V. Konyagina o shakhmatnoy raskraske” [On Some Approaches to Solving S.V. Konyagin’s Chess Coloring Problem], in Materialy nauchno-issledovatel’skogo seminara po diskretnoy geometrii i geometrii chisel, Moscow: Moscow State University, pp. 1–8.

14. Gallamov, M. M. 2019, “Straight lines 𝑦 = −𝑒 · 𝑥 + 𝑡 and chess coloring”, in Algebra, Theory of Numbers and Discrete Geometry: Modern Problems, Applications and History Problems, Tula: Tula State University, pp. 247–250.

15. Gallamov, M. M. 2019, “Straight lines 𝑦 = 1−√5/2 ·𝑥+𝑠 and chess coloring”, in Algebra, Theory of Numbers and Discrete Geometry: Modern Problems, Applications and History Problems, Tula: Tula State University, pp. 247–250.

16. Gallamov, M. M. 2020, “Straight lines 𝑦 = −[𝑎±0 ; 𝑎±1 , 𝑎±2 , . . .] · 𝑥 + 𝑡 with even 𝑎+𝑛 and odd 𝑎−𝑛= 𝑎(̸= 1) and chess coloring”, in Algebra, Theory of Numbers and Discrete Geometry: Modern Problems, Applications and History Problems, Tula: Tula State University, pp. 261–265.

17. Gallamov, M. M, 2022, “Tselochislennaya approksimatsiya otrezka” [Integer Approximation of a Segment], in Algebra, Theory of Numbers and Discrete Geometry: Modern Problems, Applications and History Problems, Tula: Tula State University, pp. 235–238.

18. Shishkin, Yu. A, 1984, Eylerova kharakteristika [Euler Characteristic], Moscow: Nauka, 96 p.

19. Vasil’ev, N. B. 1974, “Vokrug formuly Pika” [Around Pick’s Formula], Kvant, 12, pp. 39–43.

20. Vavilov, V. V, Ustinov, A. V. 2006, Mnogougol’niki na reshetkakh [Polygons on Lattices], Moscow: MCCME, 72 p.

21. Grunbaum, B., Shephard, G. C. 1993, “Pick’s Theorem”, The American Mathematical Monthly, 100(2), pp. 150–161.

22. Davenport, H. 1965, The Higher Arithmetic: An Introduction to the Theory of Numbers, New York: Harper & Brothers, 176 p.

23. Klein, F. 1987, Elementarnaya matematika s tochki zreniya vysshey. Arifmetika. Algebra. Analiz [Elementary Mathematics from an Advanced Standpoint. Arithmetic. Algebra. Analysis], 4th ed, Moscow: Nauka, 432 p.

24. Sizyy, S. V. 2008, Lektsii po teorii chisel [Lectures on Number Theory], 2nd ed, Moscow: Fizmatlit, 192 p.

25. Khovanova, T., Konyagin, S. 2011, “Sequences of Integers with Missing Quotients and Dense Points Without Neighbors”, arXiv [Preprint], Available at: https://arxiv.org/abs/1104.0441