О некоторых экстремальных задачах для целых функций экспоненциального типа
https://doi.org/10.22405/2226-8383-2025-26-1-47-61
Аннотация
В статье изучается ряд экстремальных задач для неотрицательных и интегрируемых на вещественной оси целых функций экспоненциального типа ⩽ 𝜎 (класс ℰ+1,𝜎).
Рассматриваемые задачи имеют следующий вид. Пусть Λ𝜌 – инвариантный относительно сдвига оператор с локально интегрируемым символом 𝜌(𝑥), 𝑥 ∈ R таким, что 𝜌(𝑥) = 𝜌(−𝑥), 𝑥 ∈ R. При фиксированном 𝜎 > 0 требуется найти следующие величины:
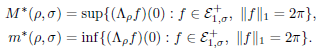
Данная общая задача сводится к равносильной экстремальной задаче для положительно определённых функций, решение которой известно. Как следствие, нами получены явные значения величин 𝑀*(𝜌, 𝜎) и 𝑚*(𝜌, 𝜎) для ряда различных символов 𝜌. В частности, рассмотрены случаи, когда Λ𝜌 – дифференциальный или разностный оператор специального вида.
Ключевые слова
целые функции экспоненциального типа,
экстремальные задачи,
положительно определенные функции,
теорема Бохнера,
преобразование Фурье.
При поддержке: Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-30012).
Об авторе
Анатолий Дмитриевич Манов
Донецкий государственный университет; Математический институт им. В. А. Стеклова Российской академии наук
Россия
Россия
кандидат физико-математических наук
Список литературы
1. Ибрагимов И. И. Экстремальные задачи в классе целых функций конечной степени // Изв. АН СССР. Сер. матем. 1959. Том 23, № 2. С. 243–256.
2. Korevaar J. An inequality for entire functions of exponential type // Nieuw Arch. Wiskunde. 1949. Vol. 23., № 2. P. 55–62.
3. Горбачев Д. В. Интегральная задача Конягина и (𝐶,𝐿)-константы Никольского // Тр. ИММ УрО РАН. 2005. Том 11, № 2. С. 72–91.
4. Carneiro E., Milinovich M. B., Soundararajan K. Fourier optimization and prime gaps // Comment. Math. Helv. 2019. Vol. 94. P. 533–568.
5. H¨ormander L., Bernhardsson B. An extension of Bohr’s inequality // Boundary value problems for partial differential equations and applications. RMA Res. Notes Appl. Math. 1993. Vol. 29. P. 179–194.
6. Горбачев Д. В. Точные неравенства Бернштейна – Никольского для полиномов и целых функций экспоненциального типа // Чебышевский сб. 2021. Том 22, № 5. C. 58–110.
7. Манов А. Д. Об одной экстремальной задаче для положительно определённых функций // Чебышевский сб. 2021. Том 22, № 5. С. 161–171.
8. Sasv´ari Z. Multivariate Characteristic and Correlation Functions. Berlin, Boston: De Gruyter, 2013.
9. Siegel C. L. ¨Uber Gitterpunkte in konvexen K¨orpern und ein damit zusammenh¨angendes Extremal problem // Acta Math. 1935. Vol. 65. P. 307–323.
10. Boas R.P. Jr., Kac M. Inequalities for Fourier transforms of positive functions // Duke Math. J. 1945. Vol. 12, № 1. P. 189–206.
11. Горбачев Д. В. Экстремальная задача для периодических функций с носителем в шаре // Матем. заметки. 2001. Том 69, № 3. C. 346–352.
12. Gabardo J.P. The Tur´an Problem and Its Dual for Positive Definite Functions Supported on a Ball in Rd // J. Fourier Analysis and Applictions. 2024. Vol. 30, № 11.
13. R´ev´esz S. G. Tur´an’s extremal problem on locally compact abelian groups // Anal. Math. 2011. Vol. 37, № 1. P. 15–50.
14. Sz´asz O. ¨Uber harmonische Funktionen und L-Formen // Math. Zeitschr. 1918. Vol. 1. P. 149–162.
15. Garsia A., Rodemich E., Rumsey H. On Some Extremal Positive Definite Functions // Journal of Mathematics and Mechanics. 1969. Vol. 18, № 9, P. 805–834.
16. Delsarte P., Genin Y., Kamp Y. Interpolation Type Problems in the Class of Positive Trigonometric Polynomials of Fixed Order // Math. Control Signal Systems. 1989. Vol. 2. P. 171–185.
17. Стейн И. Сингулярные интегралы и дифференциальные свойства функций. М.: Мир, 1973.
18. Sasv´ari Z. Positive Definite and Definitizable Functions. Berlin: Akad. Verl., 1994.
19. Trigub R. M., Belinsky E. S. Fourier Analysis and Approximation of Functions. Boston, Dordrecht, London: Kluwer-Springer, 2004.
Рецензия
Для цитирования:
Манов А.Д. О некоторых экстремальных задачах для целых функций экспоненциального типа. Чебышевский сборник. 2025;26(1):47-61. https://doi.org/10.22405/2226-8383-2025-26-1-47-61
For citation:
Manov A.D. On some extremal problems for entire functions of exponential type. Chebyshevskii Sbornik. 2025;26(1):47-61. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-1-47-61
Просмотров:
51
Послать статью по эл. почте 