On some extremal problems for entire functions of exponential type
https://doi.org/10.22405/2226-8383-2025-26-1-47-61
Abstract
In this paper we consider a number of extremal problems for nonnegative and integrable entire functions of exponential type ⩽ 𝜎 (the class ℰ+1,𝜎). The problems under consideration have the following form. Let Λ𝜌 be a translation invariant operator with a locally integrable symbol 𝜌(𝑥), 𝑥 ∈ R, such that 𝜌(𝑥) = 𝜌(−𝑥), 𝑥 ∈ R. For a fixed 𝜎 > 0, it is required to find the following constants:
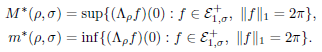
This general problem reduces to an equivalent extremal problem for positive-definite functions, the solution of which is known. As consequence, we obtained exact values of 𝑀*(𝜌, 𝜎) and 𝑚*(𝜌, 𝜎) for a number of different symbols 𝜌. In particular, we consider cases where Λ𝜌 is a differential or difference operator of a special form.
About the Author
Anatoliy Dmitrievich ManovRussian Federation
candidate of physical and mathematical sciences
References
1. Ibragimov, I. I. 1959. “Extremal problems in a class of entire functions of finite degree”, Izv. Akad. Nauk SSSR. Ser. Mat., vol. 23, no. 2, pp. 243–256. (in Russ.)
2. Korevaar, J. 1949. “An inequality for entire functions of exponential type”, Nieuw Arch. Wiskunde., vol. 23, no. 2, pp. 55–62.
3. Gorbachev, D. V. 2005. “An integral problem of Konyagin and the (𝐶,𝐿)-constants of Nikol’skii”, Trudy Inst. Mat. i Mekh. UrO RAN, vol. 11, no. 2, pp. 72–91. (in Russ.)
4. Carneiro, E., Milinovich, M. B. & Soundararajan, K. 2019. “Fourier optimization and prime gaps”, Comment. Math. Helv., vol. 94, pp. 533–568.
5. H¨ormander, L.& Bernhardsson, B. 1993. “An extension of Bohr’s inequality”, Boundary value problems for partial differential equations and applications. RMA Res. Notes Appl. Math., vol. 29, pp. 179–194.
6. Gorbachev, D. V. 2021. “Sharp Bernstein–Nikolskii inequalities for polynomials and entire functions of exponential type”, Chebyshevskii Sb., vol. 22, no. 5, pp. 58–110. (in Russ.)
7. Manov, A. D. 2021. “On an extremal problem for positive definite functions”, Chebyshevskii Sb., vol. 22, no. 5, pp. 161–171. (in Russ.)
8. Sasv´ari, Z. 2013. “Multivariate Characteristic and Correlation Functions”, De Gruyter, Berlin–Boston.
9. Siegel, C. L. 1935. “ ¨Uber Gitterpunkte in konvexen K¨orpern und ein damit zusammenh¨angendes Extremal problem”, Acta Math., vol. 65. pp. 307–323.
10. Boas, R.P. Jr. & Kac, M. 1945. “Inequalities for Fourier transforms of positive functions”, Duke Math. J., vol. 12, no. 1, pp. 189–206.
11. Gorbachev, D. V. 2001. “Extremum Problem for Periodic Functions Supported in a Ball”, Math. Notes., vol. 69, no. 3, pp. 313–319.
12. Gabardo, J.P. 2024. “The Tur´an Problem and Its Dual for Positive Definite Functions Supported on a Ball in Rd”, J. Fourier Analysis and Applictions, vol. 30, no. 11.
13. R´ev´esz, S. G. 2011. “Tur´an’s extremal problem on locally compact abelian groups”, Anal. Math., vol. 37, no. 1, pp. 15–50.
14. Sz´asz, O. 1918. “ ¨Uber harmonische Funktionen und L-Formen”, Math. Zeitschr., vol. 1, pp. 149–162.
15. Garsia, A., Rodemich, E. & Rumsey, H. 1969. “On Some Extremal Positive Definite Functions”, Journal of Mathematics and Mechanics, vol. 18, no. 9, pp. 805–834.
16. Delsarte, P., Genin, Y. & Kamp, Y. 1989. “Interpolation Type Problems in the Class of Positive Trigonometric Polynomials of Fixed Order”, Math. Control Signal Systems, vol. 2, pp. 171–185.
17. Stein, E. 1970. “Singular Integrals and Differentiability Properties of Functions”, Princeton University Press.
18. Sasv´ari, Z. 1994. “Positive Definite and Definitizable Functions”, Akad. Verl., Berlin.
19. Trigub, R. M. & Belinsky, E. S. 2004. “Fourier Analysis and Approximation of Functions”, Kluwer-Springer, Boston–Dordrecht–London.
Review
For citations:
Manov A.D. On some extremal problems for entire functions of exponential type. Chebyshevskii Sbornik. 2025;26(1):47-61. (In Russ.) https://doi.org/10.22405/2226-8383-2025-26-1-47-61






























